仿生六足机器人基于足力分布的位姿调整策略

刘海清，刘玉斌，张 赫，陈 杰，赵 杰

(哈尔滨工业大学机器人技术与系统国家重点实验室，哈尔滨150001)

六足机器人具有丰富的步态和较强的地形适应能力，能够在失去若干肢体的情况下继续行走，具有较高的可靠性和稳定性.六足机器人的稳定性主要取决于其自身的位姿，通过对位姿的实时调整，可提高机器人的步行稳定性.

六足机器人行走时为实时变化的串并联机构，运动学分析复杂，采用位置控制方法对机器人进行位姿调整难以满足实时性，且运算量大[1]，因此位姿调整通常采用力控制的方法.目前位姿调整采取的方法有悬浮控制[2－4]、力/位混合控制[5]以及力/力矩分配[6－7]等.力/位混合控制是为了使机器人腿从摆动空间平稳过渡到约束空间，力/力矩分配则是对机器人关节受力进行均衡和优化，悬浮控制则是对机器人躯干的位姿偏差进行修复.这三种方法都只是从一个侧面对位姿进行平衡和修复，缺乏对位姿的主动调整.文献[3]对四足机器人的足力控制进行了研究，六足机器人的足力控制则更加复杂，目前尚无相关研究工作.文献[8]提出通过调整足式机器人的重心位置到支撑多边形的几何中心来提高机器人的稳定性，因此可以考虑将机器人重心调整引入到位姿调整中，来对机器人进行主动位姿调整.

本文提出了基于足力分布的位姿调整策略，通过力学分析建立了机器人在任意步态模式下的足力分布模型，求得足底受力的平衡关系;采用重心位置调整来进行位姿优化，提高机器人行走时的稳定裕度，并获得期望的足力分布;然后引入虚拟悬挂模型来计算足力补偿，修复外界干扰带来的躯干位姿偏差.最后通过Adams仿真分析验证了算法的有效性.

1 六足机器人的足力分布模型

建立足力分布模型的目的是为了实现机器人足底反力的合理分布.六足机器人在任何时刻都需要至少三条腿来支撑，因此需要分析机器人三足到六足支撑时的足力分布，以建立任意足步态情况下的足力分布模型.

1.1 机器人的力学模型

六足机器人的力学模型如图1所示.全局坐标系为O－XYZ，机器人重心坐标为(xG，yG，zG);机体坐标系为[XGG，YGG，ZGG]，机器人机体位于平面XGGYGG内;足端与地面接触点为Pi=[xi，yi，zi](i为六足编号);机器人受外力F=[Fx，Fy，Fz]和外力矩M=[Mx，My，Mz]作用;足端受力为fi=[fix，fiy，fiz].

图1 仿生六足机器人力学模型

从位姿平衡角度考虑，机器人在竖直方向上的波动以及沿俯仰、侧翻方向的转动是机器人位姿的主要影响因素，这些因素与足端分布力的竖直分量fiz直接相关.于是得到下列平衡方程式:

其中，腿i为机器人的支撑腿.

1.2 三足支撑时的足力分布

当机器人为三足支撑时，设三支撑腿为A、B和C，解方程组(1)可得机器人的足力分布为:

1.3 四足支撑时的足力分布

机器人四足支撑时，力学平衡方程式(1)包含四个未知数，却只有三个独立方程，因而没有惟一解，系统不确定.针对这样的情况，需要引入额外的约束条件.通常情况下，当支撑腿均匀承担机器人的重力时，机器人的位姿稳定，承载能力大，并且能耗小[9].因此，设定足力的方差最小作为目标函数:

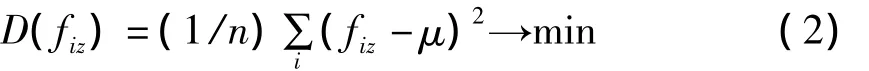
其中:μ=(1/n)∑ifiz=(Fz+mg)/n，n为机器人支撑腿数目.由式(1)和(2)可求出四足支撑时的足力分布.

1.4 五足支撑时的足力分布

五足支撑时，将式(1)代入式(2)中，通过化解消元，目标函数D变为一个二元二次多项式，不妨设函数:

将其转化为求解函数f(x，y)的最小值问题:

目标函数(3)的求解过程如下:

1)求函数在定义域内所有驻点处的函数值，驻点处函数的偏导数为零

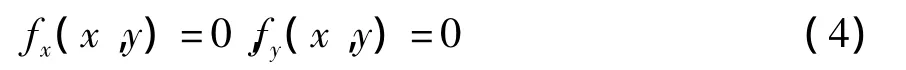
2)求函数在定义域边界上的最小值

3)比较函数值的大小，找出最小值

由于函数定义域为开区间(0，mg+Fz)，又f(x，y)为二元二次函数，则方程组(4)为二元一次方程组，存在惟一解(x0，y0)，使得函数在该点取得最小值.x0、y0也就为足力fiz其中的两个力.再代入式(1)即可求得其余的三个力，从而得到五足支撑时的足力分布.

1.5 六足支撑时的足力分布

六足支撑时，求足力分布的方法和五足支撑的解法类似，此时目标函数转化为求三元二次函数D(fiz)=f(x，y，z)的最小值，函数驻点处的偏导数为零:

方程组(5)为三元一次方程组，存在惟一解(x0，y0，z0)，使函数f在该点取得最小值.x0、y0、z0也就为fix其中的三个力，代入式(1)即可求得其余的三个力.

2 机器人重心位置调整

六足机器人要实现其非结构化地形的稳定行走，仅仅依靠足力分配是不够的，还需要配合机器人重心位置的调整，以提高其步态稳定性.六足机器人在行走时的稳定裕度越大则越稳定，在进行机器人步态设计时，对步态周期的每一分步都试图使其稳定裕度达到最大.为此，需要研究机器人在各种支撑情况下获取最大稳定裕度的条件.

2.1 六足机器人的最大稳定裕度算法

机器人三足支撑时，由稳定裕度的定义可知，当机器人重心的投影落在三角形内切圆心上时，稳定裕度为最大.

受此启发，当机器人在四足、五足和六足支撑时，支撑多边形最大内接圆的圆心即为稳定裕度最大的点.这可以通过反证法简单证明:若该圆圆心O不是稳定裕度最大的点，根据稳定裕度的定义，即存在某点O1到多边形各边的最短距离(记为R1)大于该圆半径，那么以点O1为圆心，以R1为半径的圆是多边形内接圆.显然，圆O1比O圆大，这与圆O是最大内接圆相矛盾.

为求得该点坐标，只需对多边形的任意三条边(及其延长线)构成的三角形计算其内切圆，判断该圆是否在多边形内部，穷举所有情况即可，步骤如下:

1)任取多边形三条边X、Y、Z组成三角形;

2)求出此三角形的内切圆Q;

3)检查多边形的边与圆Q是否相交.

如果检查通过，那圆Q即为多边形内最大内接圆.以四足支撑为例，如图2所示，A、B、C、D为机器人落足点，则情形I中的圆为支撑四边形内最大内接圆.

当机器人的落足点不在同一水平面时，可将各落足点投影到同一水平面上，再利用上述算法近似求得稳定裕度最大的坐标点.

图2 四足支撑时的最大稳定裕度

2.2 重心调整后的足力分布

机器人重心调整后，其足力分布也随之改变.将上节求得的重心投影坐标(xg，yg)代入力学平衡方程(1)得:

与之前的解法类似，当机器人三足支撑时，由式(6)可求得足力惟一解，对于其他支撑情况，结合目标函数D(fiz)→min即可求出各足力值.该足力大小即为机器人运动过程中期望的足力分布值，此时机器人具有最大的稳定裕度.

3 基于虚拟悬挂模型的足力补偿

通过建立机器人的虚拟悬挂模型，采用足力补偿策略来修复外界干扰带来的偏差，维持机器人的位姿稳定.

3.1 虚拟悬挂模型

如图3所示，在机器人躯干的竖直方向、俯仰和侧翻方向建立三个虚拟弹簧阻尼器，并规定躯干的高度和姿态变化为θp、θr和Δz，修复偏差所需要的力矩和力为ΔMp、ΔMr和ΔFz，则有下列方程:

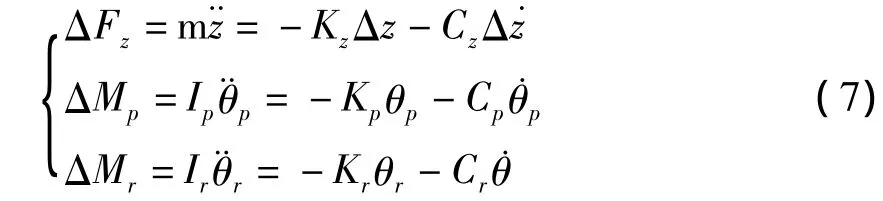
其中:Kz、Kp、Kr为虚拟弹簧的刚度(角刚度)系数;Cz、Cp、Cr为虚拟阻尼的阻尼(角阻尼)系数;m为机器人的质量，Ip、Ir分别为沿俯仰、侧翻方向的转动惯量;¨z、¨θp、¨θr分别为沿着竖直、俯仰、侧翻方向外界的干扰量.

图3 仿生六足机器人虚拟悬挂模型

3.2 足力补偿

由式(7)得系统的特征方程为:

为了提高系统的响应速度并减小超调，阻尼系数ζ应在0.7～1.0之间选择.同时，为避免外界干扰给系统给带来的共振等影响，应尽可能地增大自振频率.据此，选取自然角频率和阻尼系数为:

机器人的质量m=4.926 kg，俯仰方向的转动惯量Ip=8.978×104kg·mm2，俯仰方向的转动惯量Ir=1.157×105kg·mm2.代入上式则得

通过机器人躯干上安装的姿态传感器检测出其位姿变化，由式(7)计算出修复偏差所需的力/力矩;然后代入平衡方程(1)中，取代原来的力/力矩，并结合目标函数D(fiz)→min，即可求出各足力补偿，将该补偿值与原来的足力一起用于机器人的控制中.实际上位姿调整是一个动态过程，随着位姿的恢复，足力补偿值也逐渐趋于零.

4 仿真分析

为了验证调整算法的有效性，在Pro/e环境下建立了六足机器人和弹性路面模型，然后通过MECH/Pro接口导入到Adams环境下.机器人以三角步态行走，取占空系数为0.7，分别采用位置控制和位姿控制进行实验，仿真结果如图4～7所示.

六足机器人前进时，重心的位置变化是俯仰角上下波动的主要原因，通过重心位置的实时调整，使波动得到抑制.图4中，位置控制下，机器人起伏波动明显，而采用位姿调整后，俯仰角的波动得到明显的抑制.而翻滚角的变化则与支撑足的足力分布密切相关，通过力学模型计算出足力的合理分布，并由虚拟悬挂模型对足力进行实时补偿，修复位姿偏差.图5中，位姿控制相比位置控制的翻滚角的变化幅度更小，并且图中的斜线为位姿控制下的足力实时补偿.图6表明位姿调整提高了机器人行走时的稳定裕度，这是通过实时调整机器人重心

图6 重心稳定裕度的变化曲线

位置来实现的.图7为重心的高度变化曲线，由于位置控制在腿向前摆动的同时移动支撑腿，此时机器人六条腿都处于运动状态，因而重心起伏较大.而位姿控制由于重心调整环节的存在，摆动腿运动和支撑腿运动不是同时进行，因而重心波动小，运动平稳.

图7 重心高度的变化曲线

5 结语

基于建立的仿生六足机器人的力学模型，提出了基于足力分布的位姿调整算法.通过基于重心调整策略的位姿调整提高了机器人步行的稳定性，并且结合阻力补偿策略有效的抑制了外界的扰动，提高机器人非结构化地形的步行能力.仿真结果表明，应用该位姿调整算法提高了六足机器人行走时的稳定裕度，减小了躯干的波动，使机器人能够在非结构化地形中平稳地行走.

[1]NILSON G M，QUINN R D.Posture Control of a Cockroachlike Robot[C]//IEEE International Conference on Robotics and Automation，[S.l]:[s.n]，1998:9－14.

[2]SONG SM，WALDRON K J.Machines that walk:the adaptive suspension vehicle[M].Massachusetts London:MIT Press Cambridge，1989.

[3]KAN Y，HIROYUKI I，SHIGEO.Sky－Hook Suspension Control of a Quadruped Walking Vehicle[J].The Journal of Robotics Society of Japan，1994，12(7):1066－1071.

[4]HUANG Q J，YASUYUKI F.Posture and Vibration Control Based on Virtual Suspension Model Using Sliding Mode Control for Six－Legged Walking Robot[C]//Proceedings of the IEEE/RSJ.，[S.l]:[s.n]，2006:5232－5237.

[5]HUANG Q J，KENZO N.Neuro－Based Position and Force Hybrid Control of Six－Legged Walking Robot，Special Issue on Modern Trends on Mobile Robotics[J].Journal of Robotics and Mechatronics，2002，14(4):534－543.

[6]CHEN X D，KEIGOW，KAZUO K，et al.Optimal Force Distribution for the Legs of a Quadruped Robot[J].Machine Intelligence＆Robotic Control，1999，1(2):87－94.

[7]ERDEN M S，LEBLEBICIOGLU K.Torque Distribution in a Six－Legged Robot[C]//IEEE Transactions on Robotics，[S.l]:[s.n]，2007，23(1):179－186.

[8]CELAYA E，PORTA JM.A Control Structure for the Locomotion of a Legged Robot on Difficult Terrain[C]//IEEE Robotics＆Automation，[S.l]:[s.n]，1998:43－51.

[9]GORINEVSKY D M，SHNEIDER A Y.Force Control in Locomotion of Legged Vehicles over Rigid and Soft Surfaces[J].Int.J.Robotics Research.1990，9(2):4－23.