工程力学中杆件内力的统一简单算法

张玉梅

（赤峰学院 建筑与机械工程学院，内蒙古 赤峰 024000）

工程力学中杆件内力的统一简单算法

张玉梅

（赤峰学院 建筑与机械工程学院，内蒙古 赤峰 024000）

工程力学课程中，杆件内力的分析和计算是解决杆件强度、刚度、稳定性等问题的关键，是教学重点和难点.文章在截面法的基础上，提出了杆件内力求解的统一简单算法，给出了计算口诀，并合理定义了弯矩符号.教学实践证明，此方法便于学生理解掌握，能够大幅度提高内力求解速度，而且不易混淆忘记.

内力；截面法；统一算法

1 前言

工程力学中研究的内力是指物体因外力作用而引起的物体内部各部分间的作用力[1]，其实质是物体内力的改变量，因此也被称为附加内力[2].因课程主要研究杆件的内力，下文中把内力称为杆件内力.

杆件内力的分析与计算，是工程力学的重点内容，也是学习难点，概念抽象，内容生涩，学生理解困难，而且感到比较混乱.截面法是分析求解杆件内力的基本方法，原理清晰，但解题过程烦琐、耗时，包括截、取、代、平四个主要步骤[3]，另外，不同变形杆件的内力求解相互独立，没有直接联系，显得比较零乱.本文以截面法为基础，从杆件三种主要基本变形入手，分析、讨论并给出杆件内力分析求解的统一简单方法.

2 杆件内力求解的简单方法

2.1 轴向拉压变形

物体受力如图1（a）所示，求1-1截面内力.

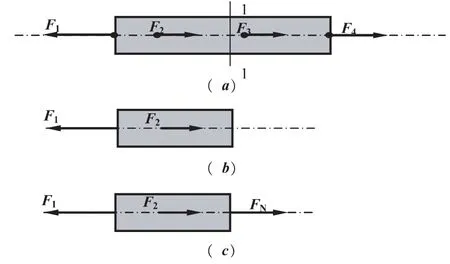
图1

首先，根据杆件受力特点——所有外力作用线均与杆件轴线共线，判断出杆件发生轴向拉（压）变形，则1-1横截面上内力是轴力，用FN表示，轴力的符号规定为拉伸为“+”，压缩为“—”.轴力的截面法求解具体如下：

第一步“截”，用一个假想平面将杆件从1-1截面截开.

第二步“取”，将截面的左侧或右侧的杆件取出，即取分离体，如图 1（b）所示.

第三步“代”，被截开截面处杆件两部分间的内力用轴力来“FN”代替，如图 1（c）所示.

最后一步“平”，根据所取分离体的受力图和平衡条件，列平衡方程，求解1-1截面轴力.具体为：

根据平衡条件∑Fx=0（x为轴线方向）列平衡方程并求解：

同理计算其它横截面上的轴力，可发现规律：任意横截面上的轴力，等于截面一侧所有轴向外力代数和，即FN=∑Fix，其中拉伸方向的外力取符号“＋”，压缩方向的外力取符号“－”.

2.2 扭转变形

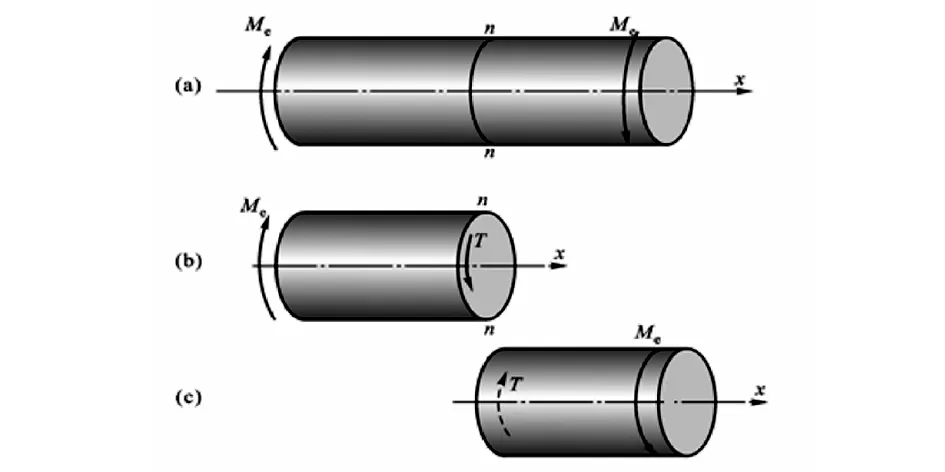
图2

如图2（a），圆轴受一组外力偶作用，求横截面n-n上的内力.

根据圆轴受力特点——圆轴在不同的横截面上受外力偶作用，可以判断出圆轴会发生扭转变形，因此截面n-n上的内力应为扭矩，用T1表示.扭矩的符号根据右手螺旋法则确定，四指与扭矩转向一致时，拇指指向截面外侧，定义为“+”，指向内侧，定义为“—”.

与轴向拉（压）变形方法相同，采用截面法进行分析和计算，分离体及受力图如图 2（b）、（c）所示.

由图2（b）根据平衡条件∑Mx=0列平衡方程并求解：

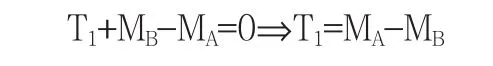
同理计算其它横截面上的扭矩，可发现规律：圆轴发生扭转变形时，任意横截面上的扭矩，等于截面一侧所有绕轴线转动的外力偶矩代数和，即T=∑Mix，其中根据右手螺旋法则判断出拇指指向外侧的外力偶矩取符号“＋”，指向内侧的外力偶矩取符号“－”.

2.3 平面弯曲变形

所谓平面弯曲变形是指当横向外力、外力偶都作用在梁的纵向对称面内，使梁的轴线在纵向对称面内弯成一平面曲线的变形情况，也称为对称弯曲变形.平面弯曲变形是弯曲变形的最基本情况，是解决弯曲变形的基础，也是工程实际中广泛存在的变形形式.

如图3（a）所示，梁AB在其纵向对称面内受到一组横向外力作用，求距A点x的截面上内力.根据其受力特点，可以判断出构件会发生平面弯曲变形，以下简称弯曲变形.根据平衡条件，可以判断出横截面内会存在剪力和弯矩两种形式的内力，剪力用Fs表示，弯矩用M表示.Fs符号规定为：绕研究对象顺时针旋转为“+”，逆时针旋转为“－”；M符号特别强调不做硬性规定，在具体计算时可任意假定，比如在下图中可以规定：使梁下侧受拉伸时取“+”，从而避免斜梁或竖梁中符号判断可能出现的混乱.

利用截面法进行分析和计算，分离体及受力图如图3

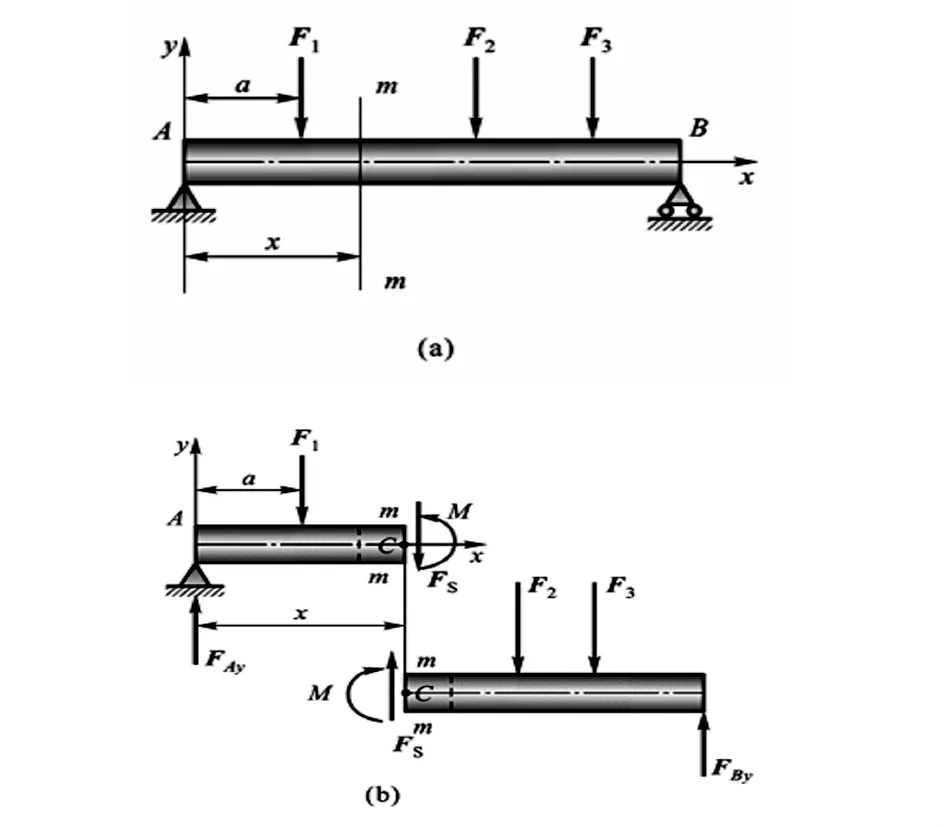
图3

（b）所示，内力全部按正号方向画出.

同理计算其它横截面上的剪力和弯矩，可发现规律：梁发生弯曲变形时，任意横截面上的剪力，等于截面一侧所有横向外力代数和，力偶不计，即Fs=∑F横向，其中相对研究对象顺时针方向旋转的取“+”，逆时针方向的取“-”；任意横截面上弯矩，等于截面一侧所有横向外力对该截面形心的力矩代数和，力偶就等于其本身力偶矩，即M=∑MC，其中与自己规定的正号弯矩作用效果的力矩取“＋”，否则取“－”.如本例中，使梁下侧受拉伸的外力矩取正.

3 杆件内力求解的统一简单算法

通过上述三种基本变形的内力分析与计算可以看出，在受力比较复杂时，内力分析起来比较麻烦，尽管参照上面各种基本变形的归纳结果，学生还是容易混乱.针对这一问题，提出下面统一求解方法：

任意一个横截面上的内力等于截面一侧相应外力（产生该种内力的外力）或外力矩代数和，数学表达式为：

F内=∑（截面一侧相应外力或外力矩），符号与前面规定一致.

4 结论

针对工程力学学习中杆件内力求解的繁琐和混乱问题，归纳总结并提出了杆件内力的统一简单求解方法，给出了计算口诀，并指出弯矩符合的更合理定义.实践教学证明，在以截面法进行理论分析推导的基础上，引领学生对统一简单方法的进行归纳总结并加以运用，使学生能够更清晰地判断杆件变形类型，更深刻地理解和掌握杆件内力求解方法，达到了快速准确解决问题的目标，同时锻炼了学生分析总结问题的能力，培养了学生主动思考、及时归纳的学习习惯.

〔1〕陈位宫.工程力学[M].北京：高等教育出版社，2008.

〔2〕张定华.工程力学[M].北京：高等教育出版社，2000.

〔3〕张庆霞，金舜卿.建筑力学[M].武汉：华中科技大学出版社，2010.

O341

A

1673-260X（2012）11-0016-02