常微分方程在数学建模中的应用
李宝萍
(安徽三联学院 基础部,安徽 合肥 230601)
常微分方程在数学建模中的应用
李宝萍
(安徽三联学院 基础部,安徽 合肥 230601)
本文介绍了常微分方程的发展,数学建模的特点,通过新产品推广模型、化工车间的通风问题模型、如何确定商品价格浮动规律模型.重点介绍了常微分方程在数学建模中的应用,总结了常微分方程在数学建模中的重要性.
常微分方程;数学建模;模型
1 引言
微分方程作为数学领域的中心学科至今已有近300年的发展历史,为了寻求、解决类似物体在自由下落过程中下落距离和时间的函数关系;研究火箭在空中飞行时的飞行轨道等这类实际性的问题,往往就要求我们找到满足某些特定条件的一个或多个未知数方程,为了解决这类实际问题从而产生了微分方程.把含有未知函数及未知函数导数或微分的方程称之为微分方程.微分方程是在处理实际问题的过程中产生的,微分方程的研究又促进实际问题的解决,同时也促进其他学科的发展.回顾微分方程的发展历史,我们发现微分方程与物理、化学、医学、生物学、天文学等方面都有着密切的联系,特别是科技的飞速发展使得微分方程的应用更为广泛.
随着社会和科技的发展,无论是在各学科,还是在各行业均涌现出了大量的、亟待人们去研究和解决的实际课题.这就要求相关的工作人员能灵活地运用数学的思维方法和知识来解决所遇到的问题,从而取得的最大的社会和经济效益.对复杂的问题进行研究、分析,并发现其中的关系及规律,同时用数学的语言表述出来,把一个实际问题转化成相关的数学问题,这个问题便称为数学模型(Mathematical Model),而把建立数学模型的过程称为数学建模(MathematicalModeling).数学建模是联系数学和实际问题的纽带,是数学在相关领域被广泛应用的媒介,数学建模有很多种分类方法,而微分方程模型是其中的重要一种.微分方程建模在解决很多实际问题时是一种特别有效的数学手段.
2 常微分方程在数学建模中的应用
用常微分方程解决实际问题一般可以分如下几步:第一步,提出实际问题;第二步,根据实际问题的规律列出相应的微分方程(即建立数学模型);第三步,解出微分方程或者对方程进行进一步定性分析;第四步,通过方程的解(或性质)来解释或者预测实际问题的发展,也就是通过数学语言来描述实际现象.下面由不同领域的几个例子来介绍常微分方程在数学建模中的广泛应用.
2.1 新产品的推广模型
在管理和经济学中,我们经常会研究关于经济量的增长、变化和边际等方面的问题,我们一般可以结合实际,再建立相应的微分方程模型,从而寻找出经济量的变化发展规律并做出相应的预测和决策,新产品的推广模型是经济学中常见的一种数学模型,下面我们来做些简要的介绍:
假设有一种新产品现在要推向市场,t时刻的销量为x(t),由于产品的性能较好,每个产品都是一个宣传品,因此t时刻产品销量的增长率与x(t)成正比,同时,考虑到产品的销售会存在一定的市场容量N,统计表明,与尚未购买该产品的顾客潜在的销售数量N-x(t)也成正比,于是有

通过分离变量、两边积分,可以解出

方程(1)称为逻辑斯谛模型,通解表达式(2)称为逻辑斯谛曲线,由
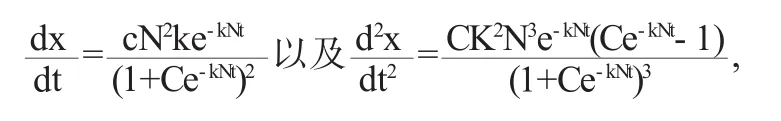
国内外很多经济学家根据调查表明,很多产品的销售曲线与公式(2)的曲线十分接近,按照对曲线的性状分析,专家认为:在新产品推出的初期阶段应采取小批量的生产并加强广告宣传力度;在产品用户达到20%至80%阶段,产品应采取大批量的生产;而在产品用户超过80%时,应做适时转产,这样才能达到最大的经济效益.
2.2 化工车间的通风问题模型
由于化工生产过程中,经常要排出一些不利于环境的物质.为了保持车间内的环境卫生,必须通入大量的新鲜空气,这就是通风问题.
设有一个30×30×12m3的车间,其中空气中含有0.12%的CO2,如需要在10分钟后CO2的含量不超过0.06%.(设新鲜空气中CO2的含量为0.04%),问每分钟应通入多少m3的新鲜空气?
解 引入下列符号:
y——时间t时CO2的浓度;
a——通入的空气量[m3/min];
v——车间的体积[m3];
y0——CO2的初浓度;
g——新鲜空气CO2的浓度;
解决这个问题主要依据下列两个物质平衡式:

现在考虑在时间间隔[t,t+dt]内CO2的进入量与排出量.由(2)式知
CO2的进入量=agdt
CO2的排出量=aydt
在瞬间t,CO2的总量等于vy;在瞬间t+dt,CO2的总量等于v(y+dy).所以在dt这段时间内,CO2的增量为v(y+dy)-vy=vdy.
根据上述分析,由(1)式可得 vdy=agdt-aydt

上述方程是一阶变量可分离方程.显然初始条件是y|t=0=y0.容易求解得

上式就是这个车间中空气中CO2的浓度y与时间t的函数关系.
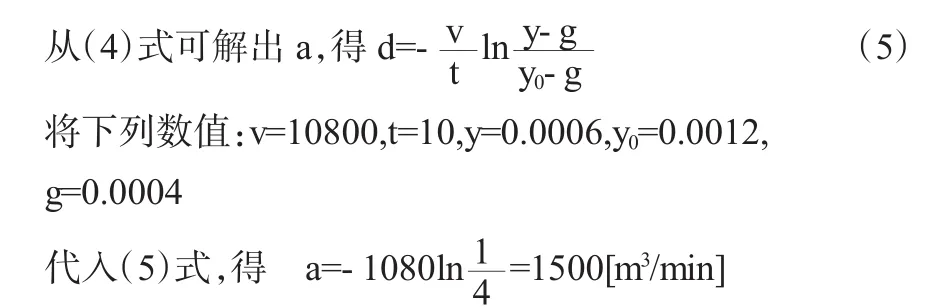
也就是说每分钟应通入1500[米3]的新鲜空气,就能在10分钟后,使车间内的CO2含量不超过0.06%.
实际上所需的新鲜空气量,比上面的数要小.因为新鲜空气并不是象假设那样很快地与混浊空气混合,而是逐步地与混浊空气混合,并且在很大程度是将它排挤出去的.
2.3 如何确定商品价格浮动规律模型
设某种商品的供给量Q1与需求量Q2是只依赖于价格P的线性函数,并假定在时间t时价格P(t)的变化率与这时的过剩需求量成正比,试确定这种商品的价格随时间t的变化规律.

其中a、b、c、d都是已知的正常数.(1)式表明供给量Q1是价格P的递增函数;(2)式表明需求量Q2是价格P的递减函数.
当供给量与需求量相等时,由(1)与(2)求出平衡价格为
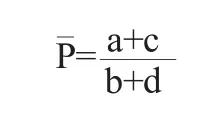
容易看出,当供给量小于需求量时,即Q1 由假定知道,P(t)的变化率与Q2-Q1成正比,即有 其中 k=α(b+d),h=α(a+c),都是正的常数. (3)式是一个一阶线性微分方程.求通解如下: 如果已知初始价格P(0)=P0,则(3)式的特解为: 上式即为商品价格随时间的变化规律. 常微分方程理论在数学建模中的广泛应用,将数学理论方法和生活实际巧妙地结合了起来,给人们提供了一种解决问题的崭新的思维方式.在解决实际问题的过程中应用微分方程理论所建立的数学模型,一般都是动态的数学模型,整个推导过程相当繁杂,但是结果极其简明,还是能提供给人们合理的解释.因此如果能有机地将常微分方程理论与数学建模结合起来,必定能使常微分方程理论在实际应用过程中发挥更大的作用、解决更多的实际问题,从而产生更好的经济效益. 〔1〕王高雄.常微分方程(第二版)[M].北京:高等教育出版社,1983. 〔2〕姜启源.数学模型(第二版)[M].北京:高等教育出版社,1993. 〔3〕李心灿.高等数学应用 205例[M].北京:高等教育出版社,1997. 〔4〕郭爽,侯丽英,李秀丽.常微分方程在数学建模中的应用[J].数学教学研究,2009(4):57-60. 〔5〕欧阳瑞,孙要伟.常微分方程在数学建模中的应用[J].宿州教育学院学报,2008(2):146-147. O172 A 1673-260X(2012)11-0-001-02 安徽三联学院2010年度院级质量工程项目(10ZIGC004)

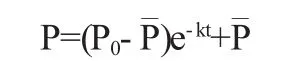
3 结束语

