超临界系统裂变增值蒙卡模拟及其时间特性分析

朱金辉 黄流兴 牛胜利

（西北核技术研究所 西安 710024）

蒙特卡罗方法可用于超临界系统的裂变增值模拟，大型蒙特卡罗模拟程序MCNP在反应堆临界分析计算中应用广泛[1‒5]。对于超临界系统，由于其中子不断增值，在进行蒙特卡罗中子输运模拟时通常需用特殊的处理方法。在MCNP中，采用裂变驿站方法[6]，通过增值系数作为校正因子以控制模拟中子数的增加，可计算给出系统的增值系数和中子平均去除时间等参数。在超临界系统分析中，反映系统参数随时间变化的增值时间常数，是超临界系统分析中的关键参数，增值时间常数与增值系数的关系也受到重点关注[7]。为反映系统增值的时间特性而开发的能模拟中子g耦合输运问题的粒子输运蒙卡模拟程序TOPAN，其中子输运模块根据ENDF/B中子截面库开发，具备裂变驿站、时间驿站、粒子标识等功能，可模拟超临界系统中的中子输运，给出超临界系统的增值系数、增值时间常数等。

本文用TOPAN程序对超临界系统进行模拟计算，给出系统的增值系数和中子平均去除时间，并与MCNP结果进行对比，验证其超临界系统计算准确性和模拟链式反应过程的可靠性。用TOPAN程序的时间驿站功能计算超临界系统的增值时间常数，并分析其与增值系数和平均裂变时间的关系。

1 系统增值系数计算

TOPAN程序中，用裂变驿站法可由增值系数的直接定义算得系统的增值系数keff，即

其中Ni是第i代裂变产生的中子总数。在每一代裂变中子输运过程中，裂变中子不再继续输运跟踪，而是存储为驿站源。在下一裂变代中子输运前，将裂变驿站源抽样得到中子输运的源粒子。经最初n代裂变中子输运后，形成较为稳定的中子分布参数。在后续裂变代的输运中根据每一裂变代源中子的总权重和产生的裂变中子的总权重按式(1)给出系统增值系数keff。

本文用一个钚球(半径r1=5 cm)外包一个钨球壳反射层(半径r2分别取5、10、15和20 cm)的简单模型。用TOPAN程序和MCNP程序计算其特征值增值系数keff，结果见表1。计算给出的增值系数keff与MCNP程序基本一致，证明TOPAN程序在链式增值反应中子输运模拟计算的可靠性。而有反射层的模型的增值系数明显大于无反射层的模型，且增值系数随着反射层厚度增加，但增值系数的增长速率随反射层厚度的增加而变慢。

2 系统中子平均去除时间计算

中子平均去除时间(逃逸、吸收或裂变)是超临界系统分析中的重要参数。TOPAN程序中用式(2)统计平均去除时间。

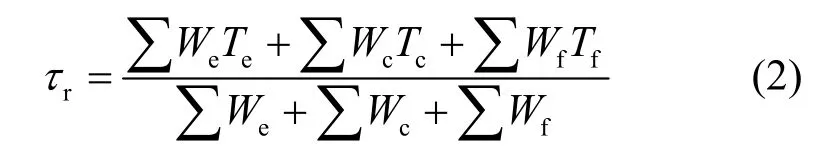
其中We和Te为逃逸粒子的权重和时间，Wc和Tc为被吸收粒子的权重和时间，Wf和Tf为发生裂变反应粒子的权重和时间，采用与§1相同的计算模型，计算给出的平均去除时间tr如表2所示。计算

表2 平均去除时间tr的计算结果*Table 2 The results of the prompt removal lifetime

得到的平均去除时间与MCNP程序计算结果相当，偏差小于 2%。同时的增加，平均去除时间随反射层厚度迅速增加，可见反射层的存在使中子输运和中子逃逸时间大大增加。

系统中子去除有三种途径：逃逸、裂变和吸收，其中裂变发生的时间对系统增值的时间特性有直接影响。TOPAN程序可以求出三种不同去除途径的平均时间及比例。定义平均逃逸时间平均逃逸时间te，平均裂变时间tf，平均吸收时间tc如下：

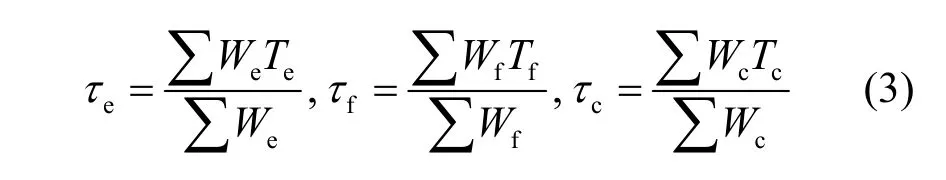
计算结果见表3。三种机制中，平均裂变时间tf最短。随反射层厚度增加，平均逃逸时间和平均吸收时间迅速增加，逃逸的权重比则不断减小。

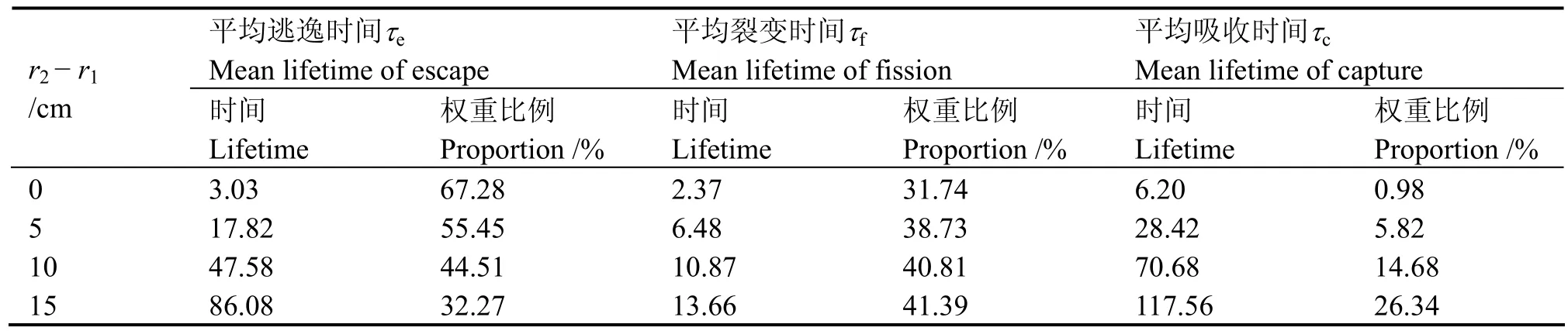
表3 不同去除机制的平均时间计算结果(单位：ns)Table 3 The results of removal lifetime(in ns) for various reactions

3 系统增值时间常数计算

对于一个超临界系统，系统增值时间常数反映其系统参数（如功率、中子数）随的时间变化。利用程序的时间驿站功能，可给出系统的增值时间常数l。基于前述模型，设14.06 MeV中子源位于系统中心，源强为8´105，取时间步长为 0.1 ns，粒子输运到时间步结束时间时存储为时间驿站源，在下一时间开始，从时间驿站源中抽样得到一定数量的源粒子开始下一时间的输运计算。由于r1=r2=5 cm的系统接近临界，将其改为r1=r2=6 cm的模型，同时取r1=5 cm，r2分别为10、15和20 cm，计算得到系统的功率随时间变化的关系如图1(a)，系统内中子数随时间的变化关系如图1(b)。

图1 系统功率(a)和中子总数(b)随时间的变化Fig. 1 The system power (a) and neutron counts (b) as function of the time.

由图1，经过最初的时间0t(10–20 ns)后，系统的功率释放和中子总数呈指数增长，即：

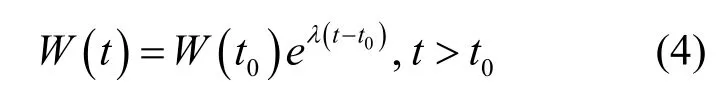
系统中的中子数随时间的变化可表示为：

实际上，系统功率增值和中子增值的时间常数l值基本一致，计算给出的结果列于表4。

表4 超临界系统增值相关参数计算结果Table 4 The multiplication parameters of the supercritical system.

4 超临界系统增值时间常数与增值系数的关系

显然，超临界系统的增值时间常数l与增值系数effk直接相关。为将上述系统的增值时间常数与其增值系数联系起来，可先考虑一种理想情况，即一代裂变中子从产生到发生下一代裂变反应的时间分布满足单一负指数分布，即

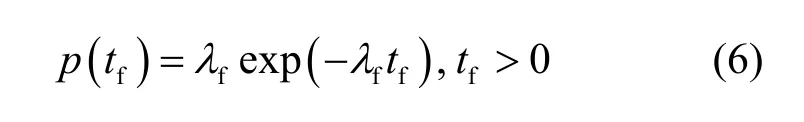
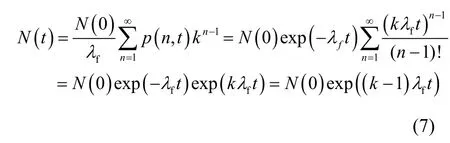
则系统每过 1/时间，系统增值 exp(k−1)倍，则系统平均裂变时间和增值时间常数值及增值系数的关系为

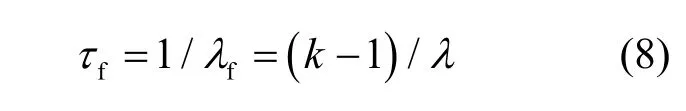
上述分析表明，系统增值时间常数主要受增值系数keff和平均裂变时间的影响。然而，式(8)的前提条件—中子裂变时间分布为单一负指数分布—与实际情况并不相符，裂变发生的时间分布可近似表示为式(9)的多指数分布

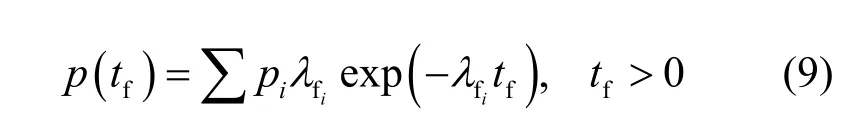
为此可参照式(8)，根据系统的增值时间常数和增值系数定义等效裂变时间为

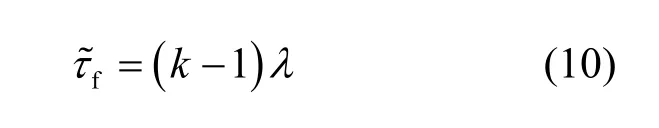
计算给出的等效裂变时间列于表4。对于不带反射层的系统，其等效裂变时间与平均裂变时间相当，略小于系统的平均裂变时间；随着放射层厚度的增加，平均裂变时间与等效裂变时间的差值逐渐增大。原因简单分析如下：裂变发生时间分布式(9)中既有下降较快的快成分，也有下降较慢的慢成分；慢成分的裂变发生时间（正比于较小）较长，使平均裂变时间增加，而对系统增值贡献（正比于）为较小；综合起来分析，系统的平均裂变时间大于等效裂变时间；对于具有较厚反射层的系统，其慢成分的发生时间可能长达数百ns甚至几个μs，大大增加了系统的平均裂变时间，从而使系统的平均裂变时间和等效裂变时间差值变得较大。

表4数据还表明，并不一定增值系数keff大的系统其系统功率的增值速度就越大，分析计算时还应考虑平均裂变时间对系统功率增值的影响。

5 小结

本文建立的蒙卡程序能够有效用于超临界系统中子输运模拟，能够给出系统增值系统、增值时间常数等参数。对于超临界系统，其系统增值时间常数除和增值系数keff有关以外，还主要受平均裂变时间的影响。实际超临界系统中的等效裂变时间一般小于平均裂变时间，随着反射层厚度增加，两者差别随之增大。

本文的计算方法可用于超临界系统增值反应相关时间特性分析，对反应堆启动和脉冲堆运行等具有一定的理论意义和应用价值。

1 李树, 谢仲生, 邓力, 等. 蒙特卡罗方法在反应堆物理计算中的应用[J], 核科学与工程, 2003, 23(2), 188-192 LI Shu, XIE Zhongsheng, DENG Li,et al. Application of Monte Carlo method in the calculation of nuclear reactor physics[J], Chinese Journal of Nuclear Science and Engineering, 2003, 23(2), 188-192

2 钟兆鹏, 施工, 胡永明. MCNP程序在反应堆临界计算中的应用[J], 核动力工程, 2003, 24(1), 8-11 ZHONG Zhaopeng, SHI Gong, HU Yongming.Application of MCNP in the criticality, calculation for reactors[J], Nuclear Power Engineering, 2003, 24(1),8-11

3 邱小平, 黎学川, 王建华, 次临界堆芯参数变化对Keff值的影响[J], 南华大学学报(自然科学版), 2005, 19(1),42-46 QIU Xiaoping, LI Xuechuan, WANG Jianhua, The Influence onKeffby parameter change in subcritical reactor[J], Journal of Nanhua University(Science and Technology), 2005, 19(1), 42-46

4 邱有恒, 邓力. 次临界a本征值计算中的时间选取方法[J], 核科学与工程, 2007, 27(2): 182-186 QIU Youheng, DENG Li. The method of selection time interval in the calculation of subcritical a eigenvalue[J],Chinese Journal of Nuclear Science and Engineering,2007, 27(2): 182-186

5 王瑞宏, 黄正丰, 江松, 等. 计算a本征值的蒙特卡罗期望估计方法[J], 核科学与工程, 2008, 28(3): 204-209 WANG Ruihong , HUANG Zhengfeng , JIANG Song,et al. Monte Carlo expected estimation method foraeigenvalue calculation[J], Chinese Journal of Nuclear Science and Engineering, 2008, 28(3): 204-209

6 Judith F. Briesmeister, Editor. MCNP-A General Monte Carlo N-particle Transport Code. Version 4B[M]. Los Alamos National Laboratory, LA-12625-M , 1997

7 邱有恒, 李茂生, 邓力, 次临界系统中a本征值与k本征值的关系[J], 清华大学学报(自然科学版), 2007,47(S1): 967-971 QIU Youheng, LI Maosheng, DENG Li, Relation ship between theaeigenvalue and thekeigenvalue in subcritical systems[J], J Tsinghua Univ (Sci & Tech) ,2007, 47(S1): 967-971