环境水样自动监测装置的效率标定及Monte Carlo模拟

潘孝兵 全 林 余小任 曲广卫 王少舜

1（西北核技术研究所 西安 710024）

2（陕西卫峰核电子有限公司 西安 710118）

在某些核废物储存装置周围，需对环境水样中的人工放射性核素进行实时自动监测。监测装置由屏蔽铅室与碘化钠g谱仪组成，对抽入铅室内的水样进行定时测量与记录，并判断目标核素特征能量g全能峰计数率的变化是否出现异常。

准确标定系统的探测效率是探测系统能正常工作的前提条件。若用放射性标准溶液标定探测系统，会产生较大量的放射性废液，而且很难对所有的目标核素都进行实验标定。较为有效的方法是采用标准溶液结合蒙特卡罗计算。利用MCNP程序，可以在较为真实的条件下，模拟能峰的高斯展宽，获得不同g能量的探测效率与峰总比等重要参数。利用较少量的标准溶液测量数据验证蒙特卡罗模型，再用该模型计算其他能量或者测量条件下的数值。

郭春营等[1]用 MCNP程序计算了 NaI(Tl)探测器的峰-总比(peak-to-total ratio)，但0.662 MeV的计算结果比实验值大 30%。肖雪夫等[2]利用蒙特卡罗法模拟了 HPGe g谱仪刻度圆柱形模型体源内放射性核素活度的校准因子。周银行等[3]对碘化钠探测器的探测效率进行了模拟计算，研究了若干种“单能源”的峰总比及能谱展宽情况。Ashrafi等[4]用GEANT程序模拟了NaI(Tl)闪烁体探测器对点源的能谱响应，又研究了含137Cs体源的响应函数。Venkataraman等[5]用MCNP4B程序计算研究了高纯锗探测器对于60–2000 keVg射线响应函数的峰-总比，与实验结果的比对证明蒙特卡罗方法的可行性。

本文建立了专用自动取样测量铅室的MC计算模型。在定时测量时，为获得探测器在铅室内对低比活度137Cs溶液的探测效率，用MCNP4C程序对探测器和铅室内部进行了模拟，并用点源模型和较高比活度的137Cs溶液实验数据验证了MC模型，基于验证的模型给出低活度水样的响应值。

1 点源测量实验与模拟

1.1 γ能谱仪

采用3R3型NaI(Tl)晶体(Φ76.2 mm´76.2 mm)，探测器的结构见图1。晶体有0.5 mm MgO反射层、2.0 mm (侧面)与2.5 mm (端面)Al反射层，以及1.0 mm不锈钢保护层。晶体与光电倍增管相连的一端是光学玻璃，厚度为2.0 mm[6,7]。

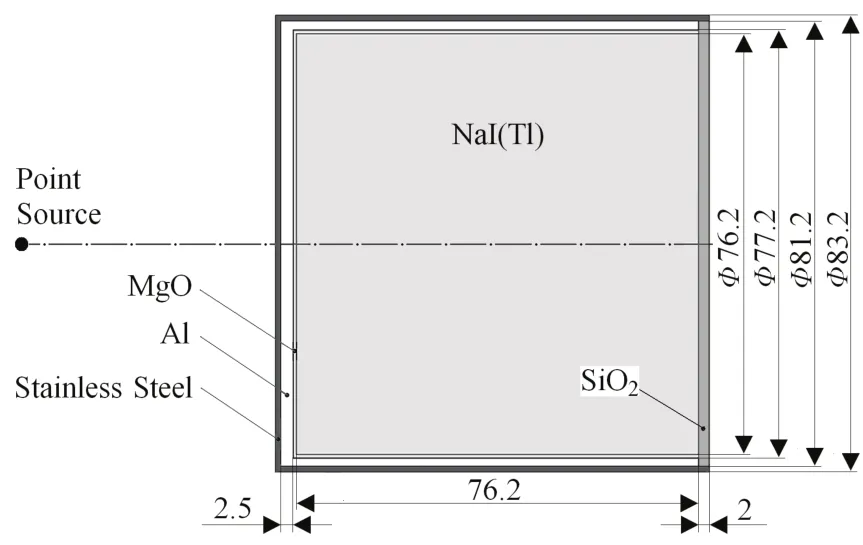
图1 NaI(Tl)探测器模型结构与材料Fig.1 The NaI(Tl) detector and materials.

g能谱仪由 NaI(Tl)探测器和数字多道能谱仪(卫峰公司)组成，0.662 MeV 的整机能量分辨率为7.5%，测量的能量范围为 0–1.8 MeV，分成 1024道。采用卫峰公司解谱软件。

1.2 点源测量实验

使用的137Cs标准源，活度为75363.20 Bq。将标准源置于探头前端中轴线上，改变源-探头距离，测定0.662 MeV的探测效率。采用本底扣除法，用该碘化钠谱仪的长时间本底测量得到单位时间的本底响应谱，用于每个g能谱的本底扣除。

1.3 模拟能谱的高斯展宽

按图1结构建立3R3型探头的蒙特卡罗模型。不锈钢为304不锈钢，密度7.93 g/cm3，含C(0.07%)、Si(1.0%)、 P(0.035%)、 S(0.03%)、 Cr(18.0%)、Mn(2.0%)、Fe(69.365%)和 Ni(9.5%)。NaI(Tl)晶体的密度为3.67 g/cm3，其中含Tl的质量为4.0%。

用MCNP4C软件中F8计数卡，可得到探测器对137Cs源的响应函数。MC模拟得到的响应函数未做高斯展宽时，0.662 MeV的全能峰近似于直线。用计数特殊处理卡 FT8，可获得展宽的能谱。3R3型探测器的能量分辨率(能峰半高宽, MeV)为[8]：式中，Eg为入射 g射线能量(MeV)，a、b、c为系数，可由实验测得的EFWHM进行拟合而得到[5]。对称性良好的高斯峰，系数a与c近似为 0。用3R3型探测器测量137Cs点源能谱，其0.662 MeV处的EFWHM=49.5 keV，据此可推算出展宽系数b=0.0608。

1.4 点源探测效率与模拟结果的对比

用该137Cs点源，调整源-探测器距离，测得3R3型 NaI(Tl)探测器在各点的探测效率，并用 MCNP程序算得的探测效率，结果见表1。实验测量137Cs点源效率的扩展不确定度2.0%。由表1，源-探测器距离3 cm时MC值与测量值偏差最大(2.8%)。MC模拟计算的效率在 1.6 %的范围内与实验值相符，这说明探测器模型是准确的。

表1 3R3型探测器对137Cs点源的源峰探测效率实验值与理论值和峰总比R(E)Table 1 Measured and simulated detection efficiency and peak-to-total ratio of the NaI(Tl) detector to the 137Cs point source.

1.5 峰总比R(E)

峰总比R(E)是能量为E的单色光子束的全能峰下的面积对整个响应函数下的全谱面积之比，其度量g射线与探测器物质进行相互作用而贡献其全部能量的概率。可用光子在晶体中沉积在E附近单位间隔的能量与沉积在晶体中的全部能量(0–E)之比来定义R(E)。而实测结果易产生误差, 因此一般实验测量要结合部分理论计算[1]。表1还给出了3R3型探测器对该137Cs点源在不同源-探距下的R(E)测量与 MCNP计算结果，可见峰总比不随源-探距而改变，其理论值平均为0.674，实验值平均为0.693，两者基本一致，且与文献[1]的理论值(0.709)较为接近。文献[1]实验值偏小(0.536)可能由并不严格的本底扣除造成。

2 铅室测量实验与MC模拟

2.1 铅室结构与实验布置

本工作的铅室内外径分别为F210 mm和F410 mm，壁厚100 mm；内衬为不锈钢，内外径分别为F194 mm和F210 mm，壁厚8 mm。探测器置于不锈钢防水套筒内，壁厚 5 mm。根据该铅室与探测器的结构，建立了其MC模型，探测器的光电倍增管、电子线路等简化为玻璃+真空，见图2。

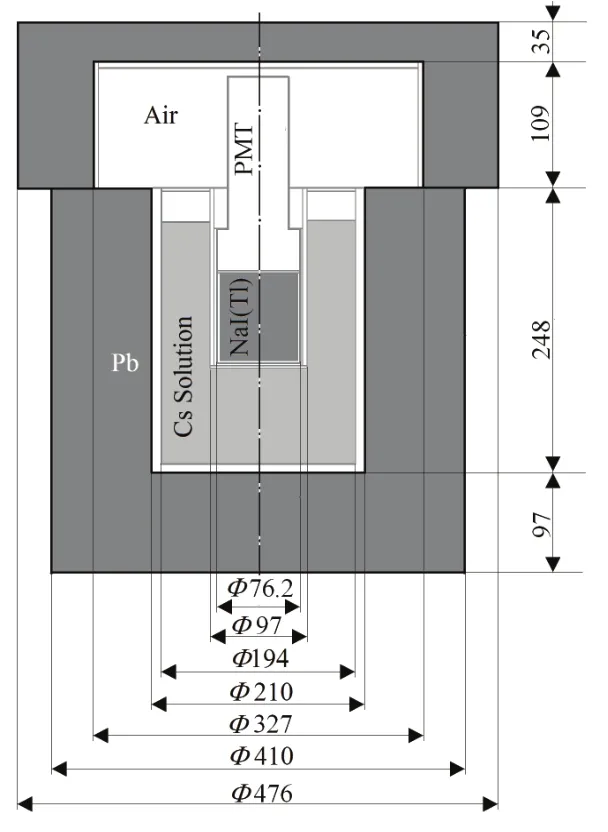
图2 蒙卡计算模型的示意图Fig.2 Model of the shielded detection system for MC simulation.

2.2 效率刻度实验与MC模拟结果的比较

实验方法是利用137Cs标准溶液，配置成比活度不同的一系列溶液(表2), 溶液体积为 5.0 L，探测器灵敏体积部分置于不锈钢套筒内。由MCNP模拟，图2模型的比活度为1 Bq/L时，探测器对0.662 MeV伽马射线的计数率为0.06774/s。

从表2可得出如下结论。

第一，137Cs溶液的比活度接近本底值时，实验值与模拟值偏差较大，这主要是因为实验不确定度较大。低浓度样品的全能峰总计数偏少（测量时间偏短），计数率的不确定度偏大。如0.07 Bq/L测得的计数率的统计误差达82%。因此在接近本底的低活度水样定时监测中，有必要根据理论计算的响应值校正实验测量结果。

第二，溶液比活度>3.77 Bq/L，全能峰的总计数增加，统计不确定度明显降低，实验值与模拟值较为接近。该MC模型在20%偏差范围内与实验值相符，验证了该模型的可靠性。由较高比活度实验验证的 MC模型计算出低活度水样的探测器响应值，可作为标准溶液标定实验结果的参考。

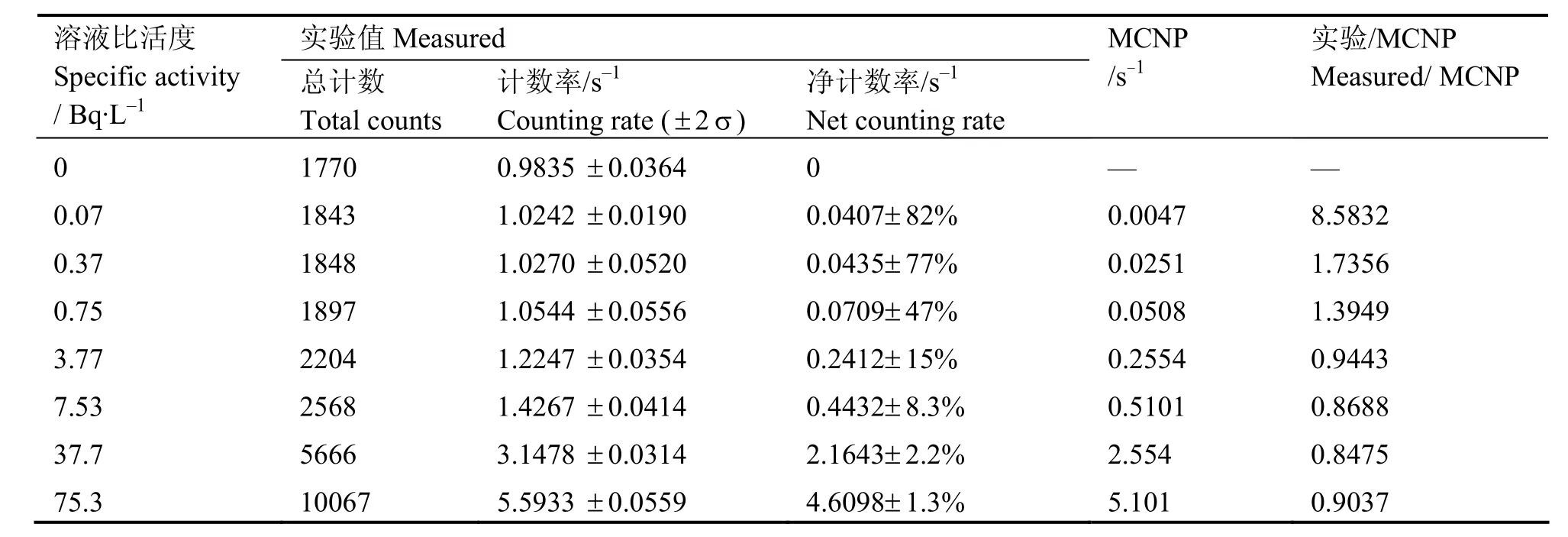
表2 3R3型探测器铅室内0.662 MeV计数率的实验值与模拟值（测量1800 s）Table 2 Measured and simulated counting rates (in 1800 s) of the shielded detector system at 0.662 MeV .

2.3 模拟伽马响应能谱

用F8脉冲计数卡及特殊处理卡FT8，记录探测器的响应，获得的铅室内碘化钠探测器对实验条件下137Cs体源的响应能谱，见图3。

由于铅室内壁材料与水的散射与吸收，低能部分的散射背景明显增强，但0.662 MeV的全能峰形状较好。模拟体源的响应能谱可以帮助我们测定水样以及土壤中天然放射性核素[4]。

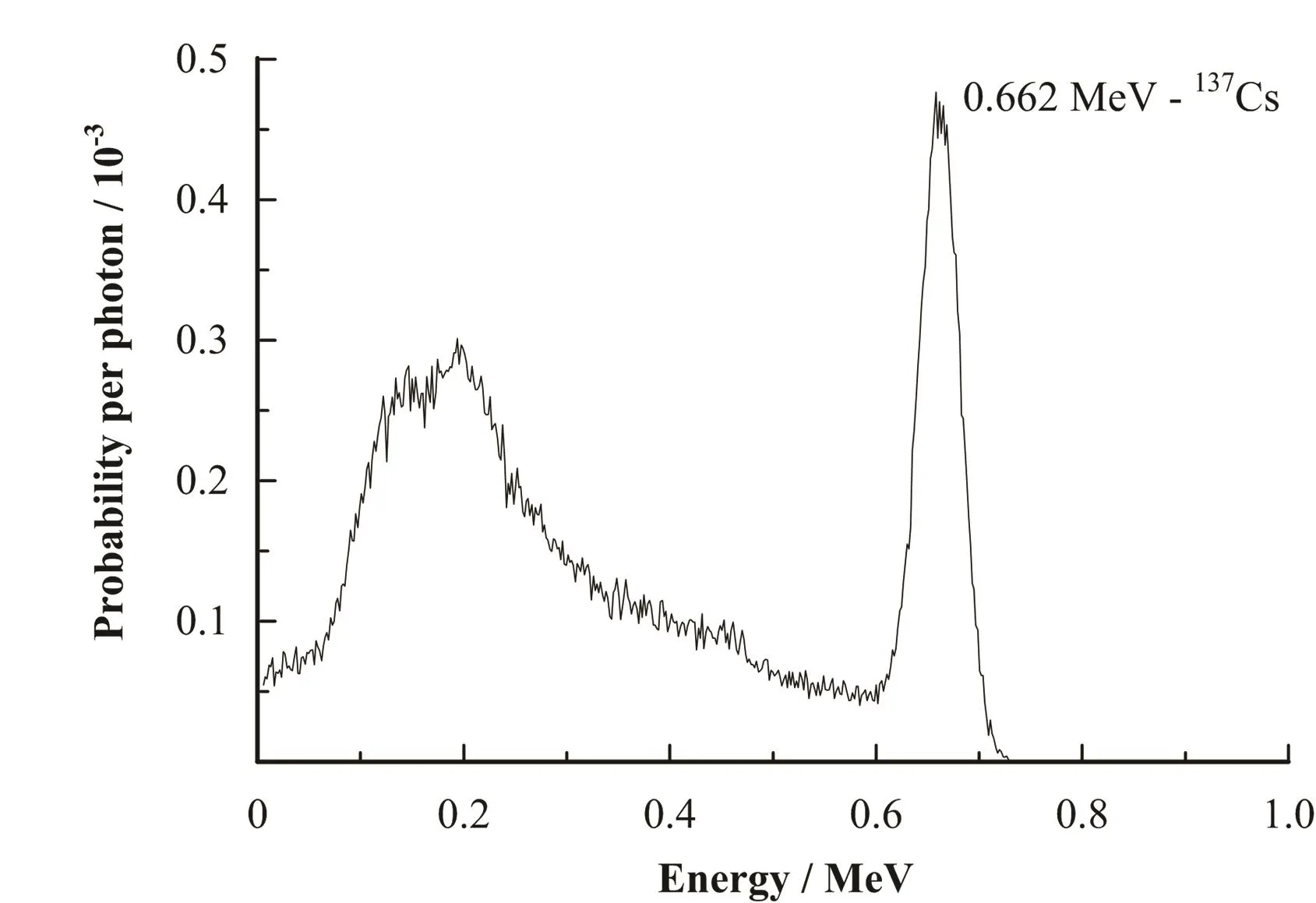
图3 碘化钠探测器在铅室中对于体源的137Cs响应模拟谱Fig.3 Simulated response spectrum of NaI(Tl) detector to 137Cs volume source in lead chamber.

3 结论

对于137Cs点源，利用较为简化的结构模型计算 NaI(Tl)探测器对点源的响应，得到不同源-探距离下0.662 MeV峰的探测效率和峰总比的模拟值与实验值基本一致。

利用铅室模型计算了上述探测器对铅室内体源(有限体源)的响应，并用较高比活度标准溶液(比活度>3.77 Bq/L)的实验数据验证了碘化钠水样取样监测系统的MC计算模型。 MC值与实验值对比，在20%的偏差范围内MC值与实验值吻合，证明计算模型较为准确。说明利用建立的MC模型研究探测器对体源的响应能谱及探测效率是可行的。

从实验数据的自洽性以及与理论值的对比可以看出，铅室测量实验存在较为明显的不足，表现为低比活度溶液的测量时间不够长，全能峰总计数偏小，造成统计不确定度较大(相对统计误差>82%)。

本文建立的实验装置与MC计算模型，可以进一步应用于对其他人工放射性核素的监测。

建议进一步研究天然放射性核素238U等对系统的干扰问题。

1 郭春营, 罗永锋, 林源根. NaI(Tl)闪烁谱仪峰总比的蒙特卡罗计算[J], 核电子学与探测技术, 2002,22(5):453–455 GUO Chunying, LUO Yongfeng, LIN Yuangen. Monte Carlo calculation of the photofractionR(E) of NaI(Tl)scintillation spectrometer[J], Nuclear Electronics &Detection Technology, 2002, 22(5):453–455

2 肖雪夫, 张积运, 马国学, 等. 环境电离模型辐射体源放射性核素活度浓度的HPGe γ谱仪就地测定[J], 辐射防护, 2003, 23(5):278–292 XIAO Xuefu, ZHANG Jiyun, MA Guoxue,et al.Measurement of radionuclide concentration in cylindrical volume sources using an in-situ HPGe γ spectrometer [J],Radialization Protection, 2003, 23(5):278–292

3 周银行, 马玉刚. MCNP能峰展宽的NaI探测效率研究[J], 核电子学与探测技术, 2007, 27(6):1062–1063 ZHOU Yinghang, MA Yugang. MCNP peak simulation of the detection efficiency of NaI [J], Nucl Electron Detect Technol, 2007, 27(6):1062–1063

4 Ashrafi S, Anvarian S, Sobhanian S.. Monte-Carlo modeling of a NaI(Tl) scintillator[J], Journal of Radioanalytical and Nuclear Chemistry, 2006, 269(1):95–98

5 Venkataraman R, Croft S, Russ W R. Calculation of peak-to-total ratios for high purity germanium detectors using Monte–Carlo modeling[J], Journal of Radioanalytical and Nuclear Chemistry, 2005,264(1):183–191

6 张婧瑶, 王南萍. NaI(Tl)闪烁探测器对铯源响应的蒙特卡罗模拟[J], 核技术, 2009, 32(11):872–874 ZHANG Jingyao, WANG Nanping. MC simulation of137Cs γ-ray spectrum of a portable NaI(Tl) detection system [J], Nuclear Techniques, 2009, 32(11):872–874

7 复旦大学编. 原子核物理实验方法[M]. 北京：原子能出版社, 1984:165/166:143–144.Briesmeister J F. MCNP–a general Monte Carlo n-particle transport code, Version-4C (Los Alamos), 3–106