闪烁体薄膜在线测量质子束流强度

张 璐 贺朝会 陈 亮 张忠兵 刘金良 任晓堂

1（西安交通大学 西安 710049）

2（西北核技术研究所 西安 710024）

3（北京大学重离子加速器实验室 北京 100871）

质子是空间辐射环境中的主要辐射，质子引发的单粒子效应会严重影响在轨航天器电子系统的可靠性。在质子单粒子效应的模拟实验中，质子束流强度的准确性关系着实验结果的可靠性。同样，质子束流的准确测量也在加速器产氚、ADS(加速器驱动次临界系统)研究中起着关键作用[1,2]。常规的束流测量方法以法拉第筒、气体电离室以及半导体探测器为主，测量原理是对束流进行收集转化，得到束流强度。法拉第筒、金硅面垒探测器、金刚石探测器等探测方法均属拦截式测量，难以反映束流强度的瞬时波动。塑料薄膜闪烁体的特点，是发光效率高、耐辐照、易加工和经济性，在剂量学中应用极为广泛。用其进行质子束流强的实时侧脸量，可减小束流强度的不稳定性对实验结果的影响。

1 闪烁体薄膜探测系统及测量原理

闪烁体薄膜探测器的原理为[3]：带电粒子或射线通过闪烁体时，会使闪烁体电离和激发，受激发分子和原子退激发时发出荧光，用光电倍增管收集这些光信号，经成形和放大就得到束流信号。经比较，我们选择美国ELJEN公司的EJ-212塑料闪烁体，用其设计了图1所示的测量系统。准直质子束射入椭球形反射罩中，打在薄膜闪烁体上，产生光信号，经光电倍增管转化，在小电流仪P中输出电流信号Ip，为探测系统输出的电流信号，代表质子在闪烁体薄膜中沉积的能量。穿透闪烁体的束流进入法拉第筒，经转换，给出单位时间收集的电荷，即电流IF。闪烁体薄膜只是减小了入射质子的能量(散射而致的束流强度减小可忽略)，对电荷影响很小，所以IF即表征束流源的强度。为确保内椭球反射罩不受外界光照的干扰，故其窗口贴铝箔以避光。光电倍增管置于内椭球焦面上，以确保光收集。

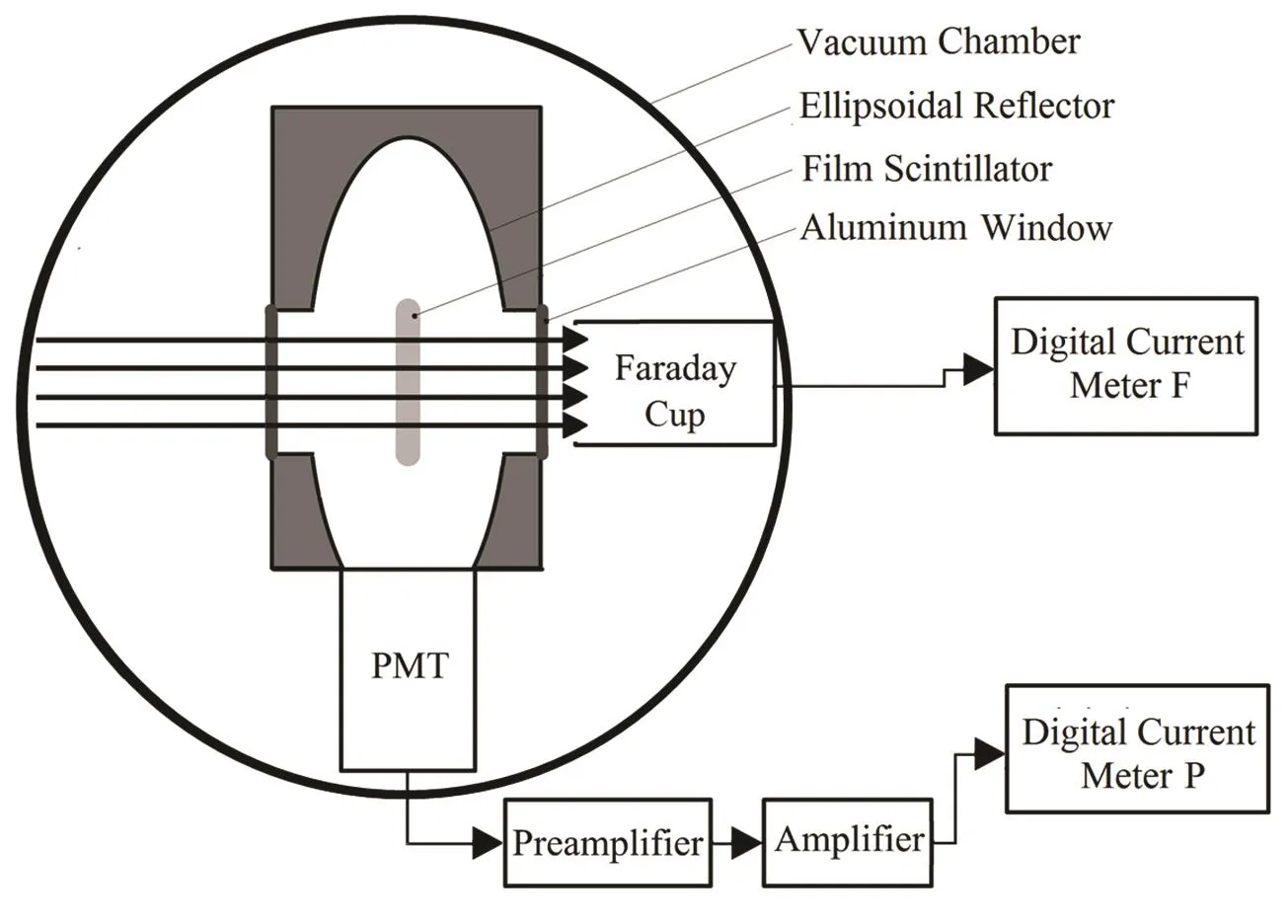
图1 闪烁体薄膜探测系统Fig.1 The scintillator film detection system.

粒子束或射线在闪烁体中损失的能量转化成光信号，闪烁体材料的光能产额Y表征闪烁体发光效率。设一个入射质子在闪烁体中消耗的能量为E，所产生的闪烁光子总数为N，则光能产额为[3]：

该质子给光电倍增管后的小电流仪P上接受的电荷为：

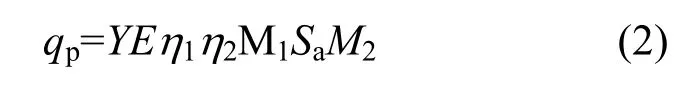
其中h1为光电倍增管对光的收集效率，h2为光电倍增管的量子效率，M1为光电倍增管的放大倍数，Sa为光电倍增管的阳极灵敏度，M2为前置放大器和主放对信号的放大倍数。

质子所带电荷为元电荷，法拉第筒探测的束流源源强。IFt个质子入射闪烁体上产生的信号为：

则

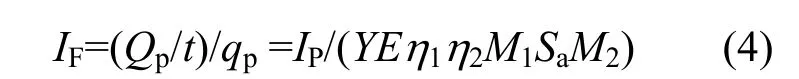
2 质子束与闪烁体材料的作用及响应

2.1 质子在闪烁体材料中的能量沉积

质子与闪烁体材料的作用过程中，核反应发生的概率相当小，对于小于400 MeV的质子束流不予考虑。在辐射探测学中，1 GeV以下的质子作用时，由轫致辐射引起的辐射能损也可忽略不计[4]。因此，只考虑其非弹性碰撞（与靶物质的核外电子的作用）和与原子核的库仑散射作用。

用TRIM计算 3–40 MeV质子在0.1 mm厚的EJ-212闪烁体中能损，用数值积分得到的能量沉积见图2。其次级电子能量为20–400 eV，与质子在该闪烁体中的能量沉积(>100 keV)相比可忽略。

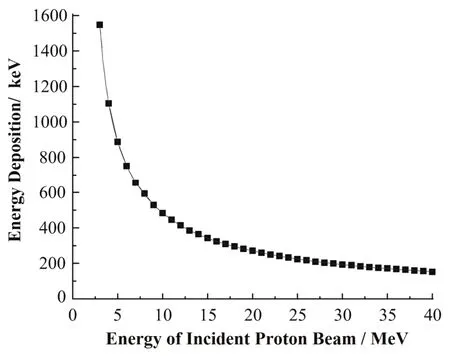
图2 3‒40 MeV质子束在0.1 mm EJ-212闪烁体中能量沉积的TRIM计算结果Fig.2 Energy deposition of proton beams at 3‒40 MeV in 0.1-mm EJ-212 scintillators, calculated TRIM code.

对上述数据用Origin 软件拟合，可得到质子入射在EJ-212闪烁体材料上的能量沉积公式，

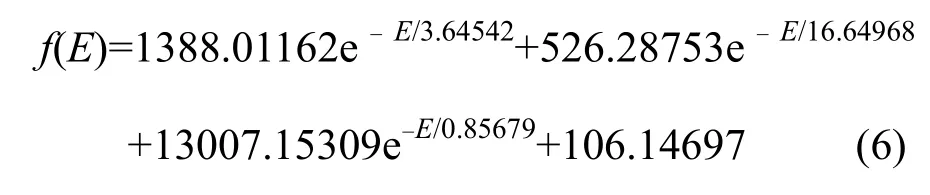
其偏差<1%，由此引起的光输出偏差<0.2%，可忽略不计，即式(6)可视为能量沉积函数。

(1)在含沙量≤3.0 kg/m3且滴灌带为一年用条件下，可采用新型泵前一级过滤与滴头抗堵新技术模式。在滴灌首部泵前安装低压旋转网式过滤器，过滤大颗粒泥沙与杂质。通过筛选出的适宜灌水器，将大部分细颗粒泥沙随滴头出水排入到田间。沉积在毛管内泥沙通过毛管尾端的辅助冲洗支管进行定时冲洗。该新技术模式改变了传统的泵后过滤器易堵塞、反冲洗频繁用水量大、压损较高的缺点。避免了因过滤而使黄河水中大量营养物质流失。运行管理维护费用低，占地面积较少，可大幅节约成本。

2.2 质子能量全沉积时EJ-212的相对光输出

描述粒子作用于闪烁体材料导致发光的很多理论都基于一个假设：粒子在物质中传输时，若电离能损较高会导致荧光过程的焠灭，使发光效率降低。而Birks[5]提出一种机制：作用过程中，若分子被破坏，就不会产生光信号，而被破坏的分子数与电离能损相关，则有：

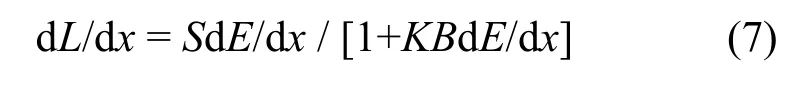
其中S为电子照射时的绝对发光效率；KB为Briks常数，需要实验确定；dE/dx为能量损失。

对于EJ-212闪烁体，S10000/MeV；其KB值[6]可取 0.009、 0.010和 0.011 g/MeV·cm2。下文对不同KB值进行了验证，发现KB0.009 g/MeV·cm2时，实验数据与理论数据的偏差最小。

同时考虑电子能损和核能损，用 TIRM 计算dE/dx，对式(7)进行数值积分，可得到不同能量的质子全部沉积在EJ-212闪烁体上时，其光子产额的响应曲线见图3。

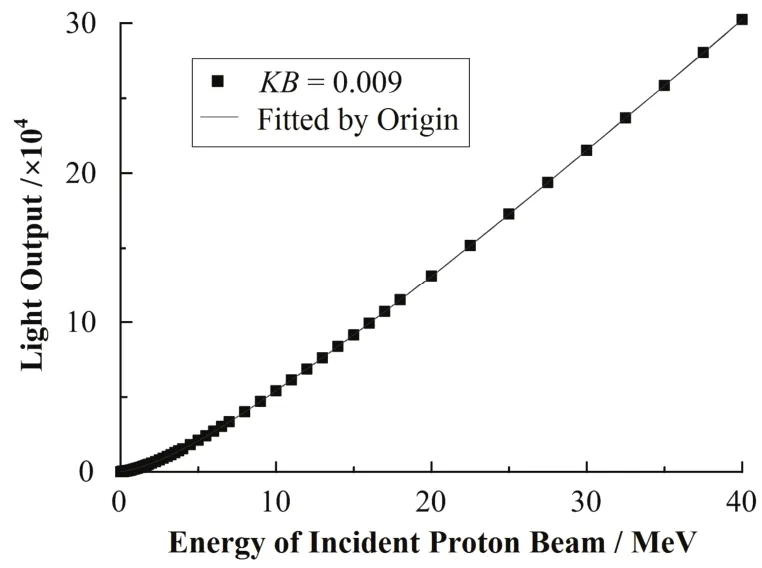
图3 全沉积时EJ-212的光输出的曲线Fig.3 The curve of light output when the whole energy deposited in EJ-212.

对图3曲线进行多项式拟合，得

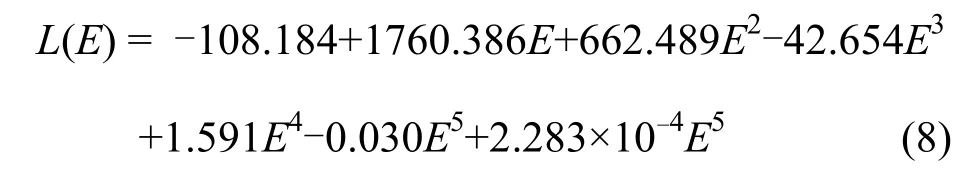
在3–40 MeV能区，由此函数计算得相对光输出的值得偏差小于 1%，由拟合曲线与实际曲线比较中偏差较大的三点(5、6、11 MeV)，这些偏差导致的在薄闪烁体部分能量沉积偏差仅为0.35%、0.36%、0.39%，所以可用此函数代替全沉积函数。

2.3 穿过闪烁体，能量部分沉积时的相对光输出

对于薄膜闪烁体，能量只是部分沉积在闪烁体内。设能量为E1的质子，穿过闪烁体薄膜后能量为E2，那么其光输出可以表示为：

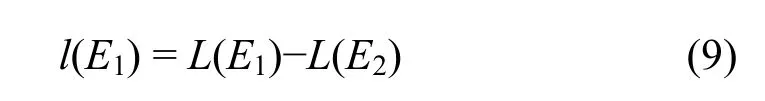
E2值由式(6)得出，按式(9)计算3–40 MeV质子在闪烁体膜中沉积部分能量的相对光输出，结果见图4。

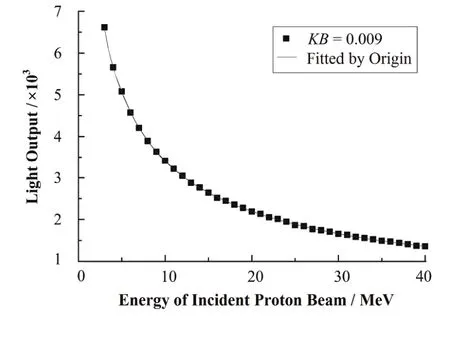
图4 部分沉积时EJ-212的相对光输出Fig.4 Relative light output when energy deposited partly.

拟合得到的函数为:

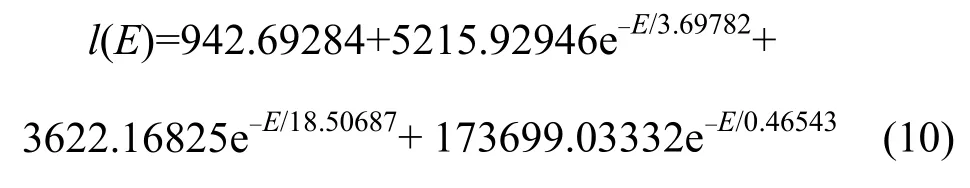
其偏差小于 1.12%。公式(5)与(10)结合，即可在测得IP的时候得到质子束流强度IF。在某一能量点，测量出IP和IF，即可标定出K值。

3 实验验证

3.1 相对光输出的验证

EJ-212闪烁体的探测灵敏度验证（用相对光输出表征）在北京学2´6 MeV串列加速器上进行，质子束能量3–8 MeV，并用金靶散射，以将轰击闪烁体的质子数控制在1000/s以内。实验装置见图5。

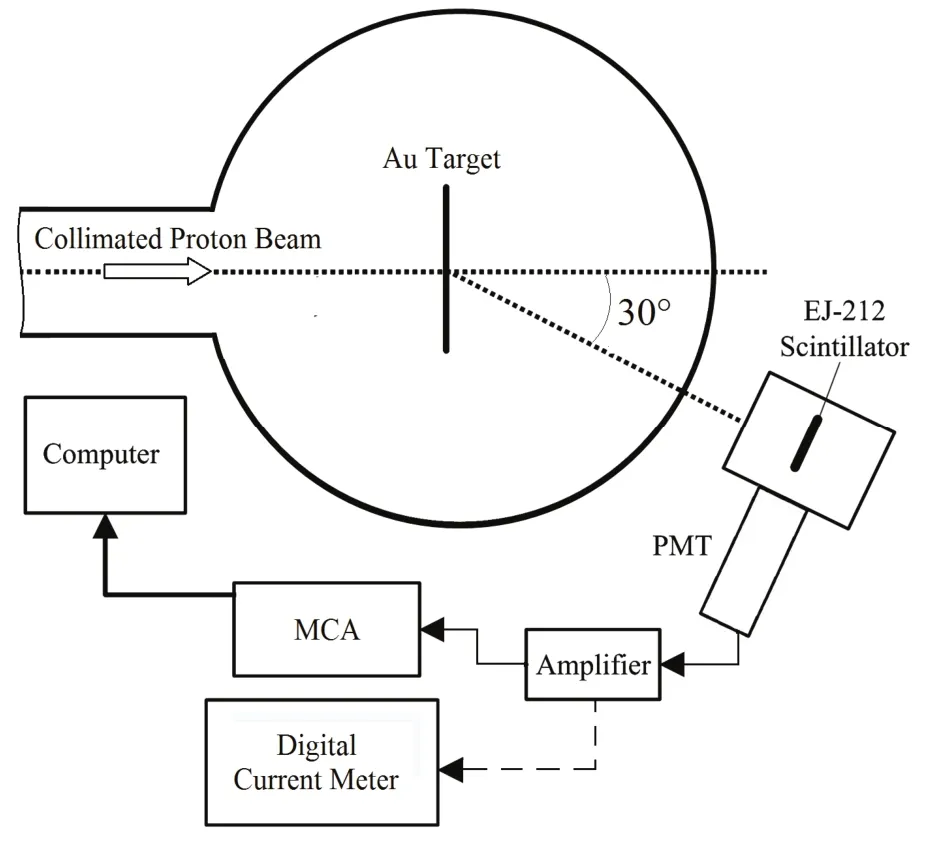
图5 脉冲信号的测量系统Fig.5 Detection system of pulse signal.

闪烁体探测系统轴心线与束流入射方向成30°角，测量时，该散射角处的束流强度视为不变。先用小电流仪测出由光电倍增管输出的5 min的电荷量，表征闪烁体探测系统测得的电流IP。再用多道分析器测出总计数，其数值相当于5 min内打在闪烁体上的质子数的总和，表征束流强度IF。再对所得谱数据和电流数据进行去噪声处理。

对比每个能量点所测得的数据，即得到在该点的探测灵敏度，最终得到变化趋势。以E5.881 MeV处的相对光输出为基准，得到其变化规律如图6所示。比较图6(a)、(b)、(c)，当KB=0.009 g/MeV·cm2时，实验数据与理论数据的偏差最小，符合得最好。

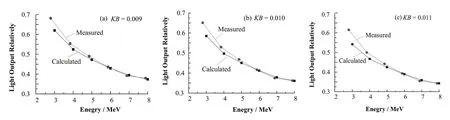
图6 BJ-212薄膜闪烁体相对光输出的实验数据和TRIM计算结果(KB= 0.009, 0.010 或 0.011 g/MeV·cm2)Fig.6 The relative light output measured and calculated by TRIM, at KB = 0.009, 0.010 or 0.011 g/MeV·cm2.

3.2 由薄膜闪烁体探测系统测得的束流源强度

法拉第筒由西北核技术研究所研制[7]，其即时探测误差<1%。对给定的加速器束流源，测量了多组数据，取偏差较小的一组(表1)进行计算，表中的If为法拉第筒上测得的电流，用于标定和比较。结合式(5)和(10)，以其中偏差最小的8 MeV的数据为基准，对系统进行标定。得式(5)的K值为23.7415。

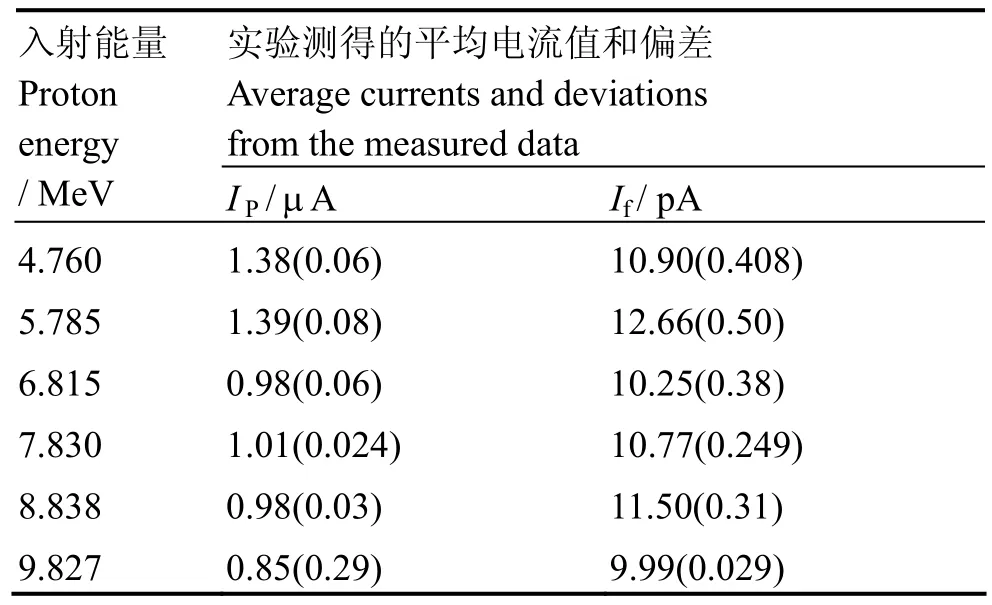
表1 不同能量下测得的IP 和IFTable 1 The value of IP and IF measured under differentenergy

当K取23.7415时，结合式(10)得到的束流源强度见表2。

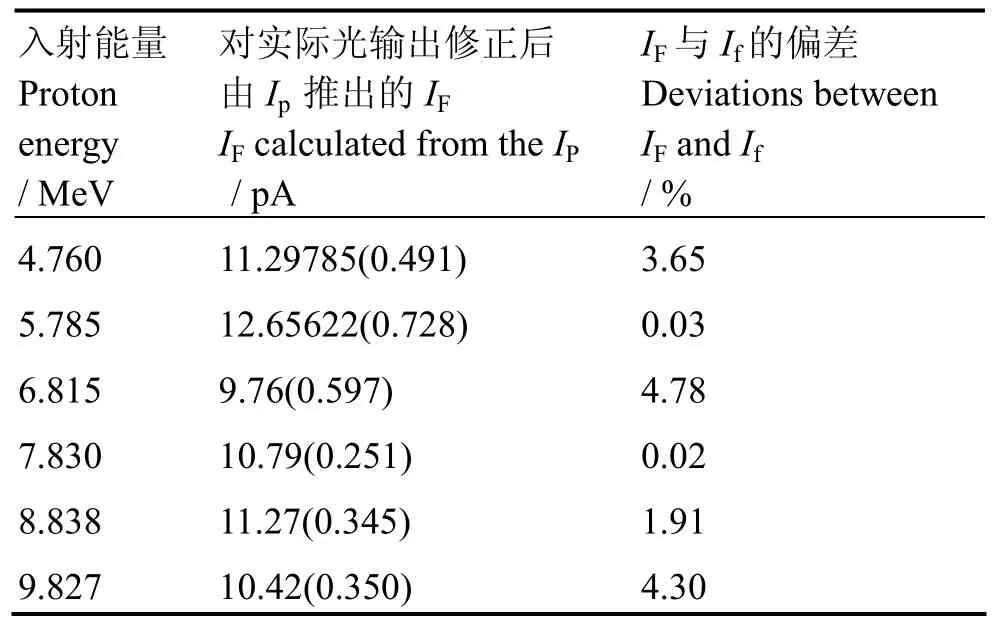
表2 由IP而得到的束流源强度IFTable 2 Intensity of proton beam(IF) calculated from the Ip

表2的IF和If表明，有闪烁体薄膜探测系统测得的束流强度与实际束流源强度相比，不确定度在5%以内。而式(10)计算的偏差在 1.12%以内。表2的法拉第筒测得的束流源强度有约为 4%的不稳定性，所以最后导致实验结果与理论结果偏差的主要原因是由束流源的不稳定性和光电倍增管的噪声。

4 结论

用闪烁体薄膜探测系统对质子束流强度进行实时在线监测，其理论探测误差在 1.12%以内，实验偏差为 5%。由于其实时在线探测的性能，束流源的波动性可以在单粒子效应等实验过程中，观察并记录到。因此，特别在束流源不稳定时，闪烁体探测系统比拦截式测量方法能更好更真实的测出束流大小，而且其测量精确性可靠，故有广泛应用前景。

1 贺朝会, 李国政, 刘恩科, 等. 北京正负电子对撞机次级束模拟单粒子效应分析[J]. 原子能科学技术, 1999,33(2): 175–181 HE Chaohui, LI Guozheng, LIU Enke. Analysis of using protons in secondary beam on BEPC as a particle source in single event effects experiment study[J]. Atomic Energy Science and Technology, 1999, 33(2):175–181

2 郭文. 中能强流质子直线加速器束流损失引起的辐射剂量问题研究[D]. 中国原子能科学研究院. 2007 Guo Wen. Research On Radiation Dosimetry Problems Caused By Beam-Loss In intermedaite-enegry High Intensity Proton Linacs[D].China Institute Of Atomic Energy, 2007

3 陈显达. 核辐射物理及探测学[M]. 北京: 清华大学工程物理系. 2004. 276–280 Chen XianDa. Nuclear Radiation Physics and Detection[M]. Beijing: Department of Engineering Physics.2004.276–280

4 Tang H K, Srinivasan G R, Azziz N. Cascade statistical model for nucleon induced reactions on light nuclei in the energy range 50MeV–1GeV[J]. Phys Rev, 1990,C42:1598–1622

5 Birks J B, The Theory and Practice of Scintillation Counting[M], Oxford: Perga-mon Press, 1967. 68–90

6 Evans H C, Bellamy E H. The response of plastic scintillators to protons[J]. Proc Phys Soc, 1959, 74:483–485

7 张忠兵, 欧阳晓平, 夏海鸿, 等. 高能质子束流强度绝对测量的二次电子补偿原理研究[J]. 物理学报, 2010,59(8): 5369–5373 ZHANG Zhongbing, OUYANG Xiaoping, XIA Honghai,et al. Accurate measurements of high energy proton beam by secondary electron compensation[J]. Acta Physica Sinica, 2010, 59(8):5369–5373