传统方法在水下相机标定应用中的研究＊

刘红坤 王江安

（海军工程大学电子工程学院 武汉 430033）

1 引言

舰船在航行过程中会在其尾部形成一条含大量气泡的白色尾迹（即尾流），有研究指出尾流中气泡的分布情况同舰船的船型、吨位、航速等有关［1］，因此对尾流气泡分布规律的研究可以为舰船目标探测跟踪、鱼雷制导以及螺旋桨空蚀的研究提供支持。由于气泡在水中是运动的，故对它的测量无法用一般的接触式方法，目前常用的方法有声学散射法、光学散射法以及摄影法等。摄影法是最为直观的方法，摄像机的标定是该方法涉及的一个关键问题。

在利用摄影技术的测量应用中，相机标定的目的是确定图像中物体的大小同实际物体大小的对应关系。之前的测量［2］大都是采用一个已知大小的物体进行拍摄比对，然后把图像中的所有像素标定为同一个值。这样做虽然简单快速，但它是以牺牲测量精度为代价的，因为成像系统是存在畸变的，一幅图像中像素的成像大小并不完全相同。利用机器视觉中的带畸变的小孔相机成像模型及标定的方法可以有效提高测量精度。

另一方面，上述测量要在海水中进行，海水的压强以及腐蚀等的影响要求必须对相机加装保护壳体才能保证其正常工作。但加装保护壳体带来了相机水下标定的相关问题。其原因是，加装保护壳体后，光线经过水、玻璃和空气再进入相机，光路发生多次折射，这使得系统的非线性复杂度大大增加，同时水和玻璃也会增加成像系统的畸变。

Cheng［3］和陈元杰［4］等人针对水下复杂的透视环境，引入了高次畸变参数对相机进行标定修正；但Tsai［5］在文献中指出，高阶畸变参数的引入并不一定是稳定和有效的；同时，上述文献也没有指出传统标定模型的精度是否适合水下相机标定应用。

针对这一问题，本文首先将在带畸变的小孔成像模型中，利用传统方法进行大气和水下的相机标定，从而验证其标定偏差的存在；接着，将采用基于神经网络的标定方法同传统标定结果进行对比研究，以分析传统标定是否满足要求。

图1 小孔成像模型

2 带畸变的小孔成像模型

小孔成像模型（如图1所示）［6～7］（pin－holemodel）是最简单的几何光学成像模型，图1中，光心为O，空间任意一点P（Xw，Yw，Zw），在摄像机坐标系下的坐标为（x，y，z），在像平面上的投影为p（X，Y）。

设图像的某像素点的坐标是（u，v），由小孔模型和相机透视模型，在齐次坐标下（Xw，Yw，Zw）和（u，v）的空间几何变换关系可表示为

其中，s为比例系数，sx、sy是CCD的像元长度和宽度，f为镜头的焦距，R和T分别为从世界坐标系到摄像机坐标系的旋转矩阵和平移向量，M为一个3×4的矩阵，称为投影矩阵，它由摄像机的内部参数决定，M2由摄像机相对于世界坐标系的方位（外部参数）决定。

小孔透视模型是一种理想的成像模型，由于摄像机光学系统不是理想的小孔模型，以及生产加工误差的存在，使得空间点在CCD上实际所成的像与理论成像点之间存在误差。为提高计算测量的精度，必须要对小孔模型进行修正，一般是在理想模型的基础上引入反映畸变的修正参数。

镜头畸变主要可以分为径向畸变、偏心畸变和薄棱镜畸变等。但在实际应用中，畸变修正参数的引入并不是越多越好，过多地引入畸变不一定能提高精度，反而会因非线性参数过多造成模型不稳定。一般的机器视觉应用中，针孔成像模型只引入径向畸变模型就足够精准，模型可表示为

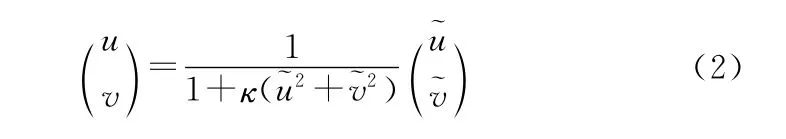
3 标定实验

3.1 传统标定实验

图2 （a）标定板图像；（b）标定板处理结果

传统标定就是寻找世界坐标系中的三维点和它在二维图像坐标系中对应的投影点，并利用这一关系求取内、外参数。本文使用平面标定板进行传统标定实验。实验中使用的标定板如图2（a）所示。

实验中，将相机和标定板的相对位置固定，首先直接进行拍摄和标定，记作空气中的标定实验；然后将一个装有盐水的玻璃水槽放置于相机和标定板之间，采集数据并标定作为水下标定实验。实验中，对于针孔相机模型中的参数，只需要考察内部参数的变化情况，因为外部参数是随环境和相机位姿等因素变化的，没有可比性。利用标定板上的黑色边界可较容易地通过阈值分割将标定板内部区域从背景中分离出来，对提取出来的部分进行边缘检测，然后将获得的数据进行拟合，求得各个标记圆的圆心，处理结果如图2（b）。将求得的对应关系代入模型即可完成标定。试验中，相机采用的是AVT Menta G－201B，镜头采用的是Computar FA 16mm／F1.4。

两次传统标定获得的相机的内部参数如表1所示。

表1 相机内部参数

表1中，f为镜头焦距，κ为镜头的径向畸变系数，sx、sy为CCD像元大小，（c0，c0）为图像坐标的主点，它们是相机的内部参数。对比数据，可以看出：一是主焦距发生了变化，另一方面径向畸变系数κ由负变正（即径向畸变的类型由桶形畸变变为枕形畸变），说明水和玻璃使得畸变复杂了。受保护壳体及水的影响，相机在水下标定的偏差是存在的。Cheng等引入高阶畸变修正量的目的是为了减小测量误差，但过多的非线性参数有时不一定会带来改善，还会使得模型求解变得不稳定。为验证传统模型和标定能否满足测量需要，使用了基于神经网络的方法进行对比试验。

3.2 基于BP神经网络的水下相机标定实验

神经网络研究兴起于上世纪40年代，目前该理论被应用到各个领域。利用神经网络进行标定是机器视觉中的一个研究热点。基于神经网络的相机标定不需要建立成像数学模型，避免因数学模型不完善带来的测量误差，有利于提高系统的精度。许多学者［10］做了很多积极有效的研究，他们的研究表明基于神经网络的相机标定有很高的精度，但他们大都没有进行数据重构的研究，因此可以用来检验传统模型及标定在水下相机应用中的有效性，但神经网络方法目前还不能很好地应用到实际的工程中。

反向传播学习算法简称 BP算法［8～10，12］，采用 BP算法的前馈型神经网络简称BP网络。BP神经网络一般由输入层、隐层和输出层组成，各层神经元之间以权值连接。各层神经元的数目和神经元的算法（激活函数）即是网络结构，它直接影响训练结果的有效性和准确性。本文将网络的大致结构设计如图3。输入层含有两个神经元，输出层含有三个神经元，隐层数从2开始，除最后一个隐层的单元个数从10个开始（最后一层的数目由输出层决定）通过不断尝试寻找误差最小的网络结构。

图3 BP神经网络结构示意图

基于神经网络的标定实验使用了一个由步进电机控制的移动平台。将平台和标定板、水槽的位置固定，相机固定在平台上（如图4所示），通过控制步进电机使相机的相对位置精确地改变。

实验中，在z＝0～10mm范围内，平台每移动1mm拍摄一次，每幅图像中49个点，通过同传统标定相同的方法获取图像中圆圈的圆心，可以获得539组训练数据。再利用Matlab的神经网络工具来实现标定数据训练。

神经网络的标定结果是无法直观地看到的，需要通过测试得知。以z＝3mm处采集所得的数据进行测试，得到如表2所示的误差情况。其中x轴方向上的误差最小，z轴上的误差最大，并且它随着标定板移动范围的变大而变大。

图4 实验平台

表2 BP网络测试结果的绝对误差

为了对比标定结果，以求取标定板上任意两圆心间的距离作参考，进行标定结果的比对。通过分析，得到误差如表3所示，其中，水下1是采用传统方法标定的结果，水下2是采用神经网络方法的标定结果。利用传统方法进行的水下标定相对空气中的误差，比采用神经网络方法所得结果的误差要好。

表3 测量结果绝对误差

4 结语

在带畸变的小孔成像模型中利用传统方法对大气和水下的相机标定的结果显示，内部参数中焦距、径向畸变系数以及主点坐标都发生了变化，说明传统标定方法在两种环境下的测量有偏差存在。基于神经网络的标定不需要建立视觉成像系统的数学模型，从而避免了因模型不完善而带来的测量误差，有利于提高系统的精度，但所得结果一定程度上依赖训练数据。例如，在本实验中当平台移动范围变大后，z轴上的误差变大很快，进而影响系统误差，另一方面，网络的训练结果同标定板标记点的密度、板的覆盖面积等因素有直接关系，如何提高神经网络标定系统的稳定性以及数据重构的研究是一个难点，因此神经网络方法目前还不很适合在工程中使用。但通过其标定结果可以看到，传统的标定方法在工程应用中的水下相机标定仍具有优势。

［1］蒋兴舟，陈喜，蒋涛.鱼雷制导设计原理［M］.武汉：海军工程大学，2001.

［2］王慧丽，张毓芬，王运鹰，等.利用光学摄影术研究尾流气泡规律进展［J］.激光与光电子学进展，2007，44（8）：68－73.

［3］Cheng Peng，Wang Jiangan，Qin Dahui.The underwater bubbles image's acquisition and processing［J］.Applied Mechanics and Materials，2010，33：152－156.

［4］陈元杰，朱康武，葛耀峥，等.基于双目视觉的水下定位系统［J］.机电工程，2011，28（5）：567－573.

［5］Tsai R Y.A versatile camera calibration technique for high－accuracy 3Dmachine vision metrology using off－the－shelf TV camera and lenses［J］.IEEE Journal of Automation，1987，3（4）：323－334.

［6］Trucco E，Verri A.Introductory techniques for 3－D computer vision［M］.New Jersey：Prentice Hall，1998.

［7］张广军.视觉测量［M］.北京：科学出版社，2008.

［8］杨彪.人工神经网络在反求中的应用研究［D］.武汉：华中科技大学，2008.

［9］史忠植.神经网络［M］.北京：高等教育出版社，2009.

［10］赵清杰，孙增圻，兰丽.摄像机神经网络标定技术［J］.控制与决策，2002，17（3）：336－338.

［11］李余琪，蒋琳琼.基于BP神经网络与粗糙集理论的分类挖掘方法［J］.计算机与数字工程，2009，37（10）.

［12］葛哲学，孙志强.神经网络理论与 MATLAB2007R实现［M］.北京：电子工业出版社，2007.