目标高精度定位技术中的摄影测量算法＊

杨 柯 赵文峰

（1.海军驻郑州地区军事代表室 郑州 450015）（2.中国电子科技集团公司第27研究所 郑州 450005）

1 引言

摄影测量的主要原理是利用摄像机摄得的图像信息来测定空间点的位置。随着数字图像处理技术的广泛应用，摄影测量的应用范围也越来越广泛。

采用合作目标，利用摄影测量原理可以进行目标高精度定位。如果合作目标数不小于4个［1～2］，或者在共面情况下合作目标不小于3个，利用单摄影测量算法就能够实现目标三维空间位置解算。本文重点将介绍利用双摄像机从被定位对象两侧，分别对多个合作目标成像并提取出其像点坐标后，利用预先标定的摄像机参数矩阵，进行目标定位。并在此基础上详细论述了双摄像测量的基本原理、数学模型及其解算方法，并就信标像点位置提取误差对测量结果的影响进行了分析。

2 双摄影测量原理

2.1 双摄影测量坐标系

图1 双摄影成像示意图

已知空间坐标系Xt，摄像机1坐标系Xc1，摄像机2坐标系Xc2。空间坐标系Xt的原点建立在朝向摄像机1一侧的长方体面的中心。水平右方向为X轴正方向；垂直向下为Y轴正方向，依据右手定则可以得到Z轴正方向。

摄像机1和2的坐标系的原点建立在光轴在CCD面的交点上，X轴的正方向是从摄像机后部观察原点向右平行于CCD水平线的方向。Y轴的正方向是从摄像机后部观察垂直向下的方向，依据右手定则可得到Z轴正方向。

2.2 双摄影测量解算方程组

由上节单摄影测量算法可以得到，摄像机1的投影方程：

假设摄像机1的内参矩阵K1已知，在式（1）两边同时乘以，可得

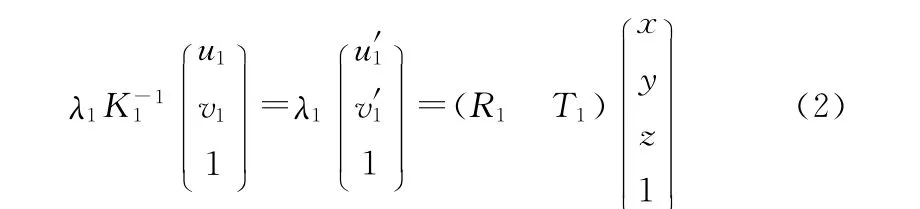
方程中消去λ1，可得下面方程（3）

同样，我们可以得到摄像机2的投影方程：

假设摄像机1坐标系与摄像机2坐标系之间的关系Rc21，Tc21已知（需事先标定），则可以推导出如下的方程式：

将式（5）代入式（4）可得：

摄像机2的内参矩阵K2已知，式（6）两边同时乘以，可得

在摄像机1下成的像点用式（3）建立方程，每个点可建立两个方程，在摄像机2下成的像点用式（7）建立方程，每个点可建立两个方程，由式（3）和式（7）联立方程组，该方程组共包含12个未知数，求解方程组即可。因此要求解该方程组最少需要3个点，可以建立6个线性方程，再加上7个约束方程，可以解得外参矩阵R和T。

3 双摄影测量目标定位解算

3.1 线性求解方法

根据摄像机1中的像点和摄像机2中像点建立的方程组，用矩阵方程表示如下：

其 中：X＝ （r11，r12，r13，r21，r22，r23，r31，r32，r33，t1，t2，t3），A是X 的系数矩阵，Q是常数矩阵。

假设像点个数是6，则A＝A16＊12，Q＝Q16＊1。

设矩阵A的最后一列为－H，即：

把H×t3移项到方程右边，整理得到

其 中：X0＝｛r11，r12，r13，r21，r22，r23，r31，r32，r33，t1，t2｝

然后，方程两边同乘A0（16×11）的广义逆矩阵，得到

因为R 是正交矩阵，RRT＝（Lt3＋M）（Lt3＋M）T＝I

令f（t3）＝（Lt3＋M）（Lt3＋M）T－I，利用最小二乘法，我们可以求得方程的解t3。

最后，将t3代入式（10）即可求出旋转矩阵和平移矩阵的各个分量。

该方法对于6个以上的像点也成立，且像点个数越多解算精度越高。

3.2 非线性求解方法

我们可以把方程（8）的求解问题转化为最优化问题的求解，最优化方程如下：

该最优化问题的求解方法可以采用Guass－Newton算法，该算法收敛很快，但对初始值的相对较高，如果初始值选择的不合适，很容易出现矩阵奇异，从而不能够求出最优解。因此，应用中采用了阻尼最小二乘法即Marquardt方法［4］。

由于非线性求解方法每次迭代都需计算广义逆矩阵，所以与线性算法相比运算量大，但求解的精度高。

4 摄影测量算法的误差分析

从以上分析中可以看出，摄影测量解算过程比较复杂，要用到的已知参数较多。影响计算结果的误差因素是很多的，很难用一个确定的误差表达式来说明这些误差源对测量结果的影响。因此采用Matlab利用假设条件对目标像点提取误差对测量精度的影响进行了分析。

假设8个合作目标组成的长方体的长＝2.15m，高＝1.5m，宽＝1.55m，长方体的8个顶点对应8个信标点；被定位目标点在世界坐标系中的坐标是（0，1.25，0）。

图2 双摄影线性解算（a）与非线性解算（b）计算误差（图中数据单位mm）

4.1 双摄影测量算法的误差分析

为了便于分析假定两摄像机相对安装（光轴重合），相距10m；摄像机1与空间坐标系之间的关系：滚转角＝pi／6，偏航角＝pi／5；俯仰角＝pi／7，空间坐标系的原点在摄像机坐标系中的坐标是（0，0，4）。通过以上条件可以求得理想像点坐标，图2中所显示的曲线是在理想像点坐标迭加一个像素的均匀分布误差时，被定位目标点解算坐标与理论坐标在x、y、z方向及空间距离上的误差。

从以上的分析结果可以知道，非线性求解方法与线性算法相比求解的精度高；并且使用非线性求解方法时，其位置测量误差不超过5cm，所以双摄影测量能够适用于近距离高精度目标定位。

5 结语

我们在随后试验过程中目标距地面高度只有2m，两摄像机相距约20m，在三个坐标方向的定位误差最大不超过4cm。从试验结果可以看出实际测量的误差与理论分析误差比较接近，测量精度能够满足实时运动目标的高精度定位要求。

可见相对于单摄影算法来说，采用双摄像机测量可以最大限度地避免系统在实际应用中由于环境因素造成目标像点丢失而无法进行目标位置解算或降低解算精度的问题，从而提高系统的冗余性、可靠性和测量精度。本文所提出的双摄影测量算法已在国内首次开展的光电引导技术预研课题中应用并取得了良好的试验效果。

［1］胡占义，雷成，吴福朝.关于P4P问题的一点讨论［J］.自动化学报，2001，27（6）：770－775.

［2］苏成，徐迎庆，李华，等.判定P3P问题正解数目的充要条件［J］.计算机学报，1998，21（12）：1084－1095.

［3］刘钦圣.最小二乘问题计算方法［M］.北京：北京工业大学出版社，1989：77－100.

［4］王爱民，沈兰荪.图像分割研究综述［J］.测控技术，2000，19（5）：21－23.

［5］Karunaseke S A，et al.A distribution measure for blocking artifacts in image based on human visual sensitivity［J］.IEEE Trans，IP，1995，4（6）：713－724.

［6］汪孔桥，Jari A.Kangas.数字图像的质量评价［J］.测控技术，2000，19（5）：14－16.

［7］罗明.多传感器机器视觉测量系统的研究及应用［M］.天津：天津大学出版社，1996：25－90.

［8］于起峰.基于图像的精密测量与运动测量［M］.北京：科学出版社，2002：1－130.

［9］刘承承，吴刚.对数字图像处理中正交变换的研究［J］.计算机与数字工程，2009，37（12）.

［10］叶建兵.基于奇异值分解的数字图像水印算法［J］.计算机与数字工程，2009，37（10）.

［11］张毓晋.图像处理和分析［M］.北京：清华大学出版社，1999：13－55.

［12］Tabatabai A J，Mitchell O R.Edge location to subpixel values in digital imagery［J］.IEEE Trans，on PAMI，1984，6（2）：188－201.