基于虚拟样机技术的机构运动可靠性分析*
陈 磊 金 超
(海装重庆局 重庆 400030)
1 引言
可靠性指标是一个装备的重要质量指标,它与装备性能指标的差别主要体现在时间上,性能指标不涉及时间因素,而可靠性指标是时间性的质量指标。面对新时期军队武器装备建设发展任务重、标准高、要求严、时间紧。传统装备以及在研装备要实现技术先进性和高质量水平的双重跨越,技术难度很大,装备可靠性已成为制约作战效能提高的最突出问题。系统地开展机构可靠性理论和分析方法的研究,并将其运用在武器装备系统的评估中,对于全面提高装备的作战效能,具有十分重要的现实意义。
在采用传统的解析法或数值仿真法对机构运动过程进行可靠性分析时,由于需要推导多个矢量方程,迭代求解非线性方程组和确定多解,解析计算过程非常复杂。特别是对于复杂的机构系统和多自由度机构,常常难以建立其解析模型[1]。而且,很多数学模型的计算本身就存在方法误差,势必会影响运算结果。本文以某型舰船动力装置液压放大机构为例,采用ADAMS虚拟样机仿真平台,进行机构运动可靠性分析。
2 虚拟样机仿真分析的基本步骤
基于虚拟样机技术的机构动作可靠性仿真,是以机构动作可靠性理论为基础,综合运用机构运动学、运动误差分析理论、干涉模型理论及虚拟样机技术,以ADAMS动力学软件[2~3]为研究平台,以实现机构动作可靠性分析及定量计算为目标的综合技术,目前已是复杂机构动作可靠性分析计算的一种行之有效的方法。

图1 虚拟样机仿真分析的基本步骤
本文针对一批完全相同的放大机构而言,考虑在尺寸制造加工误差、运动副间隙误差等各种随机因素的影响下,对液压放大机构的运动过程进行仿真,分析其机构执行末端能够准确、及时和协调地完成规定的运动的能力。只需进行机构系统建模,施加载荷和运动副约束并分析仿真结果,不需要进行该机构系统设计方面的优化分析。主要仿真步骤[4~5]有以下几步,如图1所示。
3 建立放大机构的仿真模型
3.1 创建几何模型
ADAMS/View作为ADAMS的核心模块,为用户提供了直观的建模和分析环境。虽然其三维实体建模功能相对比较薄弱,大多数研究机构都采取专业CAD软件和ADAMS联合建模的策略。而对于本文所研究的动力装置放大机构来说,将其参数化是进行运动可靠性分析的很重要的一步。对于导入的CAD模型,ADAMS/View只能自动继承质量和质心特性,不能识别形体,对于结构复杂的模型,这将给后续施加约束等工作造成很多不便;而且,最重要的一点就是,导入的模型除非进行简化,否则不能再利用ADAMS自身的功能进行参数化。
用ADAMS进行运动学仿真时,不必过分追求构件几何形体的细节部分同实际构件完全一致,只需保证各个运动部件之间的相对尺寸正确。这样既可获得较满意的运动学仿真结果,也可节约大量的几何建模时间。实际上从程序的求解原理来看,只要仿真构件的几何形体的质量、质心位置、惯性矩和惯性积同实际构件相同,仿真结果是等价的。
综合考虑以上诸因素,本文充分利用ADAMS/View提供的几何实体图形库以及强大的布尔运算功能,建立了某液压放大机构的虚拟样机模型。虽然相对使用CAD软件来讲,建模难度和工作量大大增加,但构建的模型可以根据需要实现必要的参数化,并且施加约束、运动等非常方便。
需要说明的是:由于在ADAMS零件库中没有波纹管组件,在此用等效刚度的弹簧替代放大机构中的波纹管组件。
3.2 施加约束、载荷和驱动
建立几何模型后,可以通过各种约束限制各组件之间的某些相对运动,并以此将不同构件连接起来组成整个放大机构系统。本文根据放大机构实际动作需要,在箱体上创建一个固定副;在挡板小轴和棱形轴端部之间创建一个旋转副;在顶针与波纹管的上顶针座之间创建一个点-点副;在顶针与柱体的顶针孔接触部位创建一个点-线副(因为与顶针端部相接触的是带有一定弧度的棱形轴刀口座,顶针可以在刀口座中滑动)。
要使整个放大机构能够运动起来,还需要在运动副上添加驱动和载荷,以及在构件之间施加载荷。本文利用ADAMS/View自带的STEP()函数自动拟合给定压力值,在波纹管顶端的脉冲压力小孔沿y轴负方向施加点驱动,其名称为SFORCE_1。STEP函数[6]的格式为
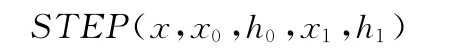
式中,x为变量,x0和x1为变量x的初始和终止值,h0和h1为对应x0和x1的函数值。其含义为

式中,h为由STEP函数自动拟合给出的值。
在SFORCE_1:Modify菜单项中编辑 Modify Force对话框:
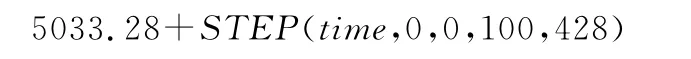
式中,5033.28表示放大机构杠杆处于平衡状态时脉冲压力值(23.52 MPa×Fa),428表示饱和蒸汽压力超过标准值2 MPa时的调节压力值(2 MPa×Fa)。
3.3 模型的参数化
参数化模型[7]是在创建模型元素(几何点、Marker点、驱动、载荷等)时,将模型元素的参数用设计来代替,设计变量的值就是模型元素参数的值,通过修改设计变量的值修改模型元素值的过程。
在生产实际中,放大机构各组件杆长、轴和孔配合间隙等参数都有相应的公差范围,而且在放大机构工作过程中,其各个联结部位施加的约束、载荷或驱动也不是极为精确的,会产生随机性误差。这些误差都有可能显著地影响整个机构系统的正常运行,在对放大机构进行运动可靠性分析时是不能忽略的。建立必要的结构尺寸在公差范围内变动的参数化模型,并将其在公差范围内随机分布的几何参数作为系统模拟分析的输入值,是进行机构运动可靠性分析计算的基础。
通过参数化建模,可以将放大机构样机模型中的参数值设置为可以改变的变量。在分析过程中,只需改变这些有关变量的值,程序就可以自动地更新整个样机模型,然后就可以对更新后的模型进行仿真,实现运动可靠性分析的目的。
3.3.1 杆件尺寸的参数化
根据放大机构模型的特点,为了方便仿真分析,这里只考虑模型中数值最大的两个力臂的长度,因为其余变量的尺寸误差相对来讲非常小,对其参数化以后,模型基本没有变化。故考虑其对应的两个变量对放大机构运动可靠性的影响较其余部分来说更为显著,本文对这两个尺寸采用设计变量方式进行参数化。
这样经过参数化以后,当修改两个设计变量的参数值时,由设计变量表述的4个结构点的坐标值会发生变化,可以看到与之相关联的对象即放大机构对应两力臂的长度也随之改变,从而达到了自动修改模型的目的。
3.3.2 运动副间隙参数化
在考虑运动副间隙误差对机构运动的影响时,要对前面建立的模型作必要的修改。本文只定义了一个旋转副,可以抽象为一个孔和轴的公差配合。本文根据ADAMS所具有的功能做出如下的改动:
以变量的形式分别参数化轴、孔半径的大小,然后通过随机性地改变变量模拟轴和孔的配合间隙,在轴和孔之间施加接触力(CONTACT)来模拟实际碰撞效果。
3.3.3 运动参数化
针对运动仿真模型而言,经过前面的尺寸和间隙参数化后,模型的修改还不完整,因为只参数化了四个点,模型中发生改变的只是与这四个点相关联的部分,其他的部分如许多布尔运算特征、所施加约束和驱动等的位置均未随之变动,所以还要对其实现运动参数化。模型中具体各标记点参数化结果表在此不一一列出。
表中所列标记点的位置和方向均已参数化,而质心标记点的位置会自动的随着模型的变化而变化,其余未列出的标记点保持原位置不变。这样,当再修改构件尺寸变量时,整个模型就会发生合理的变化。
4 放大机构运动可靠性仿真
4.1 仿真模型的验证
为了保证仿真分析顺利进行,在对放大机构进行运动仿真之前,还必须对样机模型进行最后的检验,排除在建模和参数化的过程中隐含的错误。ADAMS/View提供了一个功能强大的模型自检工具。单击菜单Tools:Model Verify命令,启动模型自检。下面是程序分析得到的模型自检结果,结果中详尽的列出了机构中总体PART的数量,机构中运动PART的数量,不同的运动副的数量,机构中总体自由度的情况等等:
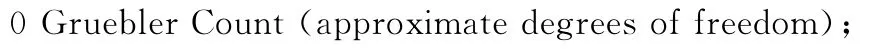
运 动 构 件 数 量:6Moving parts (not including ground);
不同的运动副数量:1Revolute Joints,1Fixed Joints,1 Higher Pair constraints,1Joint Primitives;
自由度分析:0Degrees of freedom for.modle_1
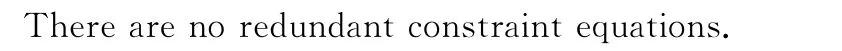
由检验结果可以验证所建立的模型是否与所要求的一致,而且可以知道模型中各个部分的连接情况,是否有多余的约束等,同时也给出了所建立的放大机构模型的系统自由度为0,可以进行运动学仿真。
4.2 编制仿真程序
对于机构运动可靠性而言,其研究对象总是针对一批机构的,由于放大机构各组件尺寸、间隙等是在一定公差范围内变化的随机值,每一个放大机构系统的组件尺寸的变动都是不同的,因此要进行多次循环仿真,具体实现过程如下:
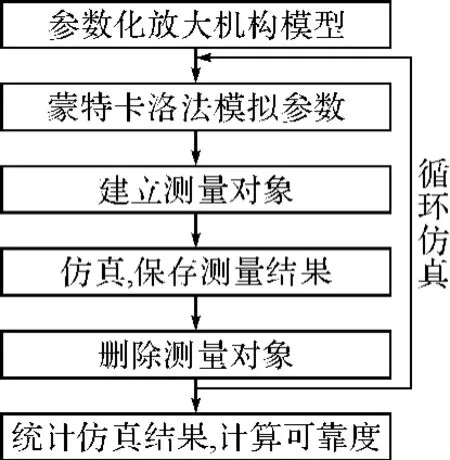
图2 放大机构运动可靠性仿真流程
本文采用ADAMS的命令语言和运行过程函数编写放大机构的运动仿真程序:
1)定义控制仿真循环次数的变量。使用ADAMS的for循环语句实现多次循环仿真,本文对100个放大机构进行仿真,即仿真100次。
2)一般认为,尺寸误差服从正态分布规律,采用蒙特卡洛法[8]模拟出服从均匀分布的随机数和正态分布抽样公式,编写一个产生服从正态分布随机数的用户自定义函数MYRAND(),在ADAMS中可以直接调用。
3)建立测量对象。本文建立放大机构挡板中心点(MARKER_22)的位移测量,在默认状态下,ADAMS/View显示测量参数随时间变化的输出曲线图,实时记录和显示测量参数值。
4)运行仿真并输出结果。本文设置仿真步长为0.1s,设置参数仿真分析停止的绝对时间为10s,整个分析过程中共输出的步数“steps”为100。
5)删除测量。因为每次仿真以后改变了原始的样机模型,如果不删除每次测量结果,则在下一次仿真时,测量名称就会重复,程序运行出现错误。
6)将模型还原。每进行一次仿真,就相当于更换了一个放大机构,但是所研究的这批放大机构所有参数都是相同的,只是每次仿真时受各种随机因素的影响所产生的结果各不相同。因此,在每仿真一次后,要将放大机构还原为原来参数再进行下一次仿真。
整个程序利用记事本存储为.cmd文件,ADAMS运行时读取该文件就可执行程序,自动进行仿真。
4.3 仿真分析结果后处理
ADAMS软件仿真分析结果的后处理,是通过调用独立的后处理模块ADAMS/Postprocessor来完成的。通过后处理模块,可以对仿真结果做进一步的分析,如可以绘制各种仿真分析曲线并进行一些曲线的数学和统计计算;可以通过图形和数据曲线比较不同条件下的分析结果;可以对结果曲线图进行各种编辑等等,以便于用户对仿真计算的结果进行观察和分析。
本文设置在对放大机构每进行一次运动仿真后,ADAMS自动生成并保存测量中心点的位移分析结果,最后得到挡板中心点的平均位移输出图。

图3 只考虑尺寸误差时挡板中心点的位移曲线

图4 同时考虑尺寸误差和间隙误差时放大机构挡板中心点的位移曲线
由曲线图可以看出,只考虑尺寸误差时,放大机构的挡板位移在饱和蒸汽压力变化值较大时其调节值已超过0.6mm,不符合规定的技术标准。而在同时考虑尺寸误差和间隙误差的情况下,放大机构的挡板位移在饱和蒸汽压力变化值较大时其调节值在规定的技术标准范围内,只是在饱和蒸汽压力变化值较大时,放大机构末端挡板位移变化并不是十分明显,显然此时液压控制系统的调节动作不够灵敏。
因此,在针对该型蒸汽动力装置的液压控制系统放大机构进行运动可靠性分析时必须考虑间隙误差的影响。通过末端位移曲线的变化可以看出,在机构的设计生产中要严格控制运动副的间隙,不能过大也不能过小,间隙过小会造成实际机构动作过大,超过规定的技术标准;间隙过大会造成调节系统的动作反应灵敏度不够,而且在实际操作过程中,也要避免饱和蒸汽管路的调节压力过大,也就是要避免动力装置空载或负荷过小的情况。
按照计算可靠度的方法[9],对仿真分析结果进行统计计算:
根据误差的表达式

通过对仿真结果的统计计算可得到输出位移误差的分布参数为

其中,i为仿真次数,Δyi是第i次位移误差,y*是不考虑误差时的标准值,yi是考虑误差时第i次仿真的仿真测量值,μ是根据仿真结果得到的运动误差的均值,σ2是根据仿真结果得到的运动误差的方差。
据此,通过对仿真结果文件中的数据进行统计处理,可以得到放大机构挡板运动误差的均值μ和方差σ2。
式中,μ0、σ是允许极限误差的分布特征值,μ、σ2是以上根据仿真结果文件统计计算出来的运动误差的分布特征值。
按照上述计算方法,本文进行放大机构运动仿真后,根据生成的结果文件,应用Matlab[11]软件编程得到了放大机构在两种不同情况下的运动可靠度曲线,如图5、图6所示。
图5 只考虑尺寸误差时的放大机构运动可靠度曲线

图6 同时考虑尺寸误差和间隙误差时的放大机构运动可靠度曲线
由曲线图可以看出,基于虚拟样机技术仿真得到的放大机构运动可靠度与采用数值算法仿真得到的运动可靠度相比,其可靠度值要稍低。可能主要由于采用的虚拟样机技术软件在进行实际机构的运动仿真时,由于考虑放大机构各组件的尺寸误差和间隙误差,机构在仿真运动时存在碰撞和运动延迟,导致其可靠度相对根据物理模型得出的可靠度要稍低。
在纵向比较放大机构在两种不同情况下的运动可靠性时,由曲线图可以明显看出在同时考虑尺寸误差和间隙误差时的放大机构运动可靠度相比只考虑尺寸误差时的放大机构运动可靠度要低,说明运动副间隙误差对机构的运动可靠性影响是较大的,在进行可靠性研究时不能忽略。
由于本文添加驱动采用的STEP()函数方式,外部载荷压力随着仿真次数由0逐步增加至428N。由曲线图可以看出,放大机构的运动可靠度基本呈缓慢增加的趋势,在外部载荷压力达到一定值后迅速下降。由于对整个放大机构进行了模型简化和假设,在载荷较小时,挡板位移不明显,机构动作很小,其可靠度值相对较低。在载荷较大时,挡板位移超出了规定的技术标准,其可靠度值迅速下降,因此在装备实际操作过程中应尽量避免动力装置载荷过大的情况。
5 结语
本文是假设放大机构各杆件具有足够的刚度,未考虑杆件变形对机构运动误差的影响。通过基于虚拟样机技术的可靠性仿真分析,对实际装备给出了使用和维修性建议。在以后的研究中,可以考虑将放大机构模型改为弹性体,仿真分析杆件变形对放大机构运动可靠性的影响。此外,还可以考虑ADAMS的二次开发[12],直接将仿真后的结果文件在ADAMS后处理模块中得到可靠度曲线。
[1]赵竹青.平面四杆机构的可靠性分析[J].应用技术与实例分析,2002(1):53-56.
[2]李军,邢俊文,覃文洁.ADAMS实例教程[M].北京:北京理工大学出版社,2002.
[3]郑建荣.ADAMS—虚拟样机技术入门与提高[M].北京:机械工业出版社,2002.
[4]候红玲,赵永强,魏伟锋.基于ADAMS的平面杆机构运动分析与仿真[J].机械,2005,32(6):33-35.
[5]郭辉.基于ADAMS的3-RPS型并联机器人虚拟样机技术的研究[D].长春:东北大学,2004.
[6]陈立平.机械系统动力学分析及ADAMS应用教程[M].北京:清华大学出版社,2005.
[7]于霖冲,白广忱,焦俊婷.空间站展开机构虚拟样机仿真及可靠性分析[J].系统仿真学报,2007,19(1):78-80.
[8]方再根.计算机模拟和蒙特卡洛方法[M].北京:北京工业学院出版社,1997.
[9]罗继曼,孙志礼.盘形凸轮机构运动可靠性模型的研究[J].机械设计与制造,2002(3):11-13.
[10]肖尚勤,郭正松.基于支持向量机的船舶结构可靠性分析[J].计算机与数字工程,2010,38(10).
[11]冯康.数值计算方法[M].北京:国防工业出版社,1978.
[12]CAO X J.Reliability Research of Clamp Outfit Based on ADAMS in the Course of Movement[J].Development &Innovation of Machinery & Electrical Products,2008,21(4):105-107.

