基于MSWF的初始投影向量估计方法研究＊

史文森 朱 海 彭汉国

（1.海军潜艇学院航海观通系 青岛 266042）（2.海军潜艇学院训练中心 大连 116085）

1 引言

信号子空间估计问题已经成为阵列信号处理中的关键问题之一。传统的信号子空间估计方法通常是对观测数据协方差矩阵进行特征值分解（EVD），对应大特征值的特征向量张成信号子空间，其余特征向量张成噪声子空间。然而EVD的计算复杂度非常高，运算量为O（NM2＋M3），其中M为观测数据的维数，N为形成协方差矩阵的采样支持长度［1］。在工程应用中M和N 的维数一般较大，该方法具有较大的计算量，这给工程实现带来了不便［2］。Goldstein等人在1998年提出了多级维纳滤波（Multistage Wiener Filter—MSWF），它是一种有效的降维滤波技术［3～4］。多级维纳滤波具有许多优点：不需要估计接收信号的协方差矩阵、前向递推的次数可以小于阵列的阵元数以及收敛速度快等。但多级维纳滤波需要给定某一目标（或用户）的信号波形（或训练序列），并以此为基础进行子空间分解［5～6］。在阵列天线信号处理的过程中，目标信号的波形、波达方向（DOA）等先验信息不易获得。通常选用接收信号的时域平均作为初始估计值，这种方法将引起较大的子空间估计误差［7～8］。

针对多级维纳滤波的特点，本文提出了初始投影向量估计的新方法。该方法以接收信号的时域平均作为初始估计值，然后进行两级维纳滤波，利用估计得到的数据构造新的初始投影向量。利用新的初始投影向量作为维纳滤波的初始值，能够大大提高子空间估计的精度。

2 基于MSWF的信号子空间估计

2.1 信号模型

假设天线阵列有M个阵元，接收到L个远场窄带信源的信号，则M个阵元接收到的信号矢量可以表示为

其中，si（t）表示第i个信号源；a（θi，φi）表示第i个信号源的导向矢量；n（t）为噪声矢量，噪声假设为时域白、空域白的零均值平稳高斯过程，并与信号不相关。

2.2 多级维纳滤波器［3］（MSWF）

MSWF是一种有效的降秩算法，其不需要对观测数据协方差矩阵求逆即可得到维纳－霍夫方程的渐近最优解，甚至不用计算观测数据协方差矩阵［9］。图1给出了MSWF前向递推的过程。

MSWF前向递推的流程为

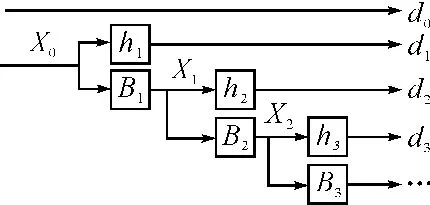
图1 MSWF前向递推的过程

通常s1（k）无法直接得到，d0（k）可由以下两种形式估计得到［10］：

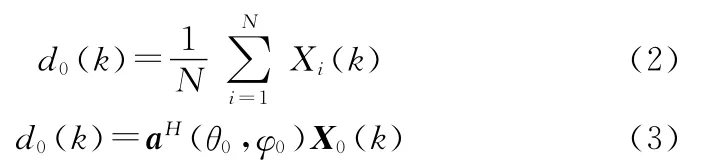
其中，a（θ0，φ0）为某一信号源的导向矢量。通常接收信号的先验信息未知，从而无法利用式（3）准确估计d0（k）。

利用MSWF算法，通过D次前向递推就可以得到D个正交向量｛h1，h2，…，hD｝，则由其张成的信号子空间为：span｛h1，h2，…，hD｝

3 初始投影向量估计

首先利用式（2）作为期望信号的估计值，进行两级维纳滤波，如图2所示。

图2 两级维纳滤波器结构图

在第一级维纳滤波中可得第一级投影向量为

其中，a（θ0，φ0）为真实的投影向量；aΔ为估计值与真值之间的误差。

经过一级维纳滤波后可得：

进行第二级维纳滤波后可得：

其中，分子中第一项可表示为

分子中第二项可表示为

其中：

其中，K1表示X0在a（θ0，φ0）方向上的投影，K2表示X0在aΔ方向上的投影，从中可以看出，K1和K2均为标量；Aopt和AΔ分别为真实的方向矢量和误差方向矢量。

从而可得h2的分子为

由于h2的分母仅起到归一化的作用，本文为了计算方便取消对h2的归一化，即：

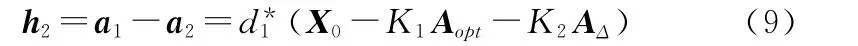
进一步计算可得到d2为

由h1与h2正交可得：

由式（4）、（6）、（9）和（11）可得方程组：

解此方程组可得：

或

由于K1表示X0在a（θ0，φ0）方向上的投影，可认为K1＞K2，于是K1和K2的取值为

从而可得：

从而可得准确的初始导向矢量为

以矢量作为初始投影矢量可得初始期望信号为：

将此时估计得到的d0（k）作为多级维纳滤波的初始期望信号进行多级维纳滤波即可。

4 仿真实验

仿真实验的条件和参数为：1）天线阵列是半径为9.5cm的7元均匀圆阵；2）接收信号的载波中心频率为16MHz，采样率为65MHz；3）与信号互不相关的背景噪声被假设为平稳的均匀复高斯随机过程，并且有零均值和方差，信噪比为；4）蒙特卡罗实验次数为5000。

子空间的估计性能采用两个指标来评价：1）子空间维数估计值n；2）估计信号子空间与真实信号子空间的距离dist。

实验1：信号源的个数为1，其信号DOA为a（10°，30°），信噪比的变化为0～30dB，变化的间隔为3dB。在每个信噪比下经过5000次蒙特卡罗实验。

图3 信号子空间维数随信噪比变化情况

图4 信号子空间距离随信噪比变化情况

实验2：信号源的个数为2，其信号DOA为a（10°，30°），a（100°，45°），信噪比的变化为0～30dB，变化的间隔为3dB。在每个信噪比下经过5000次蒙特卡罗实验。

图5 信号子空间维数随信噪比变化情况

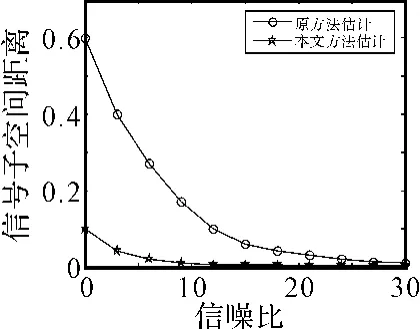
图6 信号子空间距离随信噪比变化情况

实验3：信号源的个数为3，其信号DOA为a（10°，30°），a（100°，45°），a（200°，60°）信噪比的变化为0～30dB，变化的间隔为3dB。在每个信噪比下经过5000次蒙特卡罗实验。

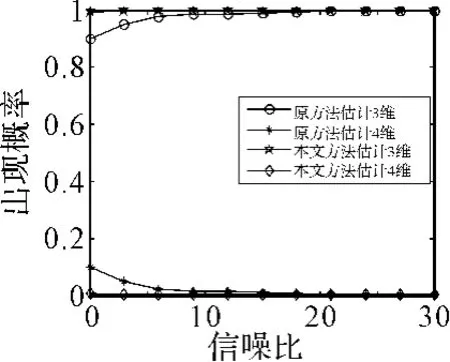
图7 信号子空间维数随信噪比变化情况

图8 信号子空间距离随信噪比变化情况

比较上述3个实验可知：1）当信号子空间的维数较小时，多级维纳滤波采用传统的方法估计期望信号，可能会导致估计出的子空间维数错误。若在多级维纳滤波前先进行1次二阶的维纳滤波，得到新的期望信号，可以提高正确估计子空间维数的能力；2）利用本文提出的方法估计得到的子空间的准确性较高；3）在低信噪比时信号子空间估计的误差较大，随着信噪比的增大，信号子空间估计的误差减小。

5 结语

本文针对多级维纳滤波初始期望信号估计值误差较大的特点，提出了一种初始投影向量估计的新方法。理论分析表明该方法可以准确地获得初始投影向量，提高子空间估计的精度，而且没有增加工程实现的难度。大量的仿真实验表明利用该方法获得初始投影向量后的多级维纳滤波器性能有了很大改善。特别是当信号子空间维数较小时该方法的优点更加突出。

［1］黄磊，吴顺君，张林让，等.快速子空间分解方法及其维数的快速估计［J］.电子学报，2005，33（6）：977－981.

［2］庄学彬，陆明泉，冯振明.一种数值稳健且低复杂度的信号子空间估计新方法［J］.电子与信息学报，2011，33（1）：90－94.

［3］GOLDSTEIN J S，REED I S，SCHARF L L.A Multistage Representation of the Wiener Filter Based on Orthogonal Projections［J］.IEEE Transactions on Information Theory，1998，44（7）：2943－2959.

［4］丁前军，王永良，张永顺.一种多级维纳滤波器的快速实现算法－迭代相关相减算法［J］.通信学报，2005，26（12）：1－4.

［5］WANG R，YAO M，CHENG Z，et al.Interference cancellation in GPS receiver using noise subspace tracking algorithm［J］.Signal Processing，2011，91（2011）：338－343.

［6］WERNER S，WITH M，KOIVUNEN V.Householder Multistage Wiener Filter for Space－Time Navigation Receivers［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，40（3）：975－988.

［7］刘敏，金光明，戴旭初.一种基于多级维纳滤波的信号子空间快速估计方法［J］.中国科学技术大学学报，2009，39（8）：792－797.

［8］龚文飞，孙昕，吴嗣亮.多级嵌套维纳滤波自适应降维STAP抗干扰方法研究［J］.宇航学报，2010，31（10）：2360－2366.

［9］丁前军，王永良，张永顺.自适应阵列中多级维纳滤波器的有效实现算法［J］.电子与信息学报，2006，28（5）：936－940.

［10］黄磊，吴顺君，张林让.基于多级维纳滤波器的信号子空间拟合算法［J］.电子与信息学报，2005，27（8）：1120－1197.