论初等函数的定义
潘玉恒,杨珂玲
(1.武汉工业学院 工商学院,湖北 武汉 430065;2.湖北经济学院 统计与应用数学系,湖北 武汉 430205)
引言
初等函数是初等数学、高等数学共同研究的对象,它具有良好的连续(极限)、可导、可积等局部性质,所以判断一个函数是不是初等函数,是解决与这个函数有关问题的关键。在现行的数学分析或高等数学的教材中,对初等函数的定义如下:
定义1:“由基本初等函数经过有限次的四则运算与复合运算所得到的函数”。[1]
定义2:“由常数和基本初等函数经过有限次的四则运算和有限次的函数复合步骤所构成并可用一个式子表示的函数”。[2]
上述定义1、2都是不严密的,例如它们在学界所引起的主要歧义点就是分段函数是否是初等函数这一问题,无论怎样,由定义引起这一问题的本身就证明了其定义是不严密的;不仅如此,定义1、2实际上还存在着理论上的缺陷,例如像这类直接改变(基本)初等函数的定义区间而得到的函数,是不是初等函数?初等函数的定义竟然没有包含这种情形,也许就是这一缺陷,才导致人们在处理分段函数的方法上复杂化了。笔者限于手上的资料,发现前贤们集中讨论了分段函数是否是初等函数的问题,而不是探讨怎样严密初等函数之定义,所以也就忽略了定义的理论缺陷,因此,笔者认为,在初等函数的定义上,还有一些问题值得商榷。
1.分段函数是否是初等函数的问题
分段函数是否是初等函数本来不应该成为一个问题,这是因为,即使是利用不严密的定义1和2,都可以直接判断分段函数不是 “由基本初等函数经过有限次的四则运算与复合运算所得到的函数”,所以不是初等函数;但由于定义2强调了“可用一个式子表示”——如果善意地理解樊映川和同济大学高等数学编写组的前贤们的本意,应该就是为了排除分段函数是初等函数的可能的,否则,凡是“由基本初等函数经过有限次的四则运算与复合运算所得到的函数”都必然是“用一个式子表示”的,即,定义1和2实际上是等价的——实在有画蛇添足之嫌,这不应是学界使用了近五十年、印刷75次的教材所应该有的纰漏,就是这“纰漏”,不曾想到却开启了人们研究分段函数能否“可用一个式子表示”的问题。
例如分段函数
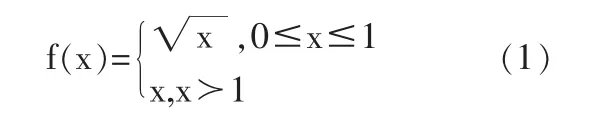
可以等价地表示为:
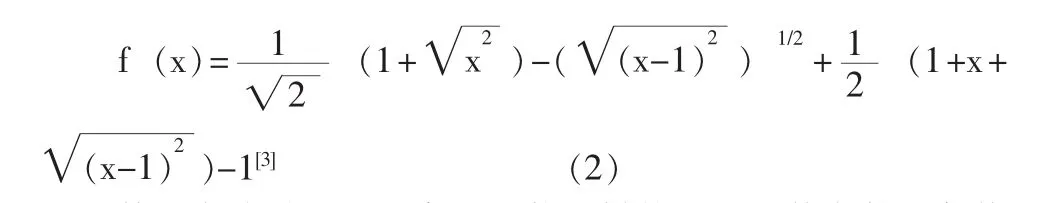
甚至有些学者还研究出了什么样的分段函数在什么条件下“可用一个式子表示”并给出了相应的定理。例如,笔者通过维普、万方数据库等搜索到较早讨论这一问题的刘文、刘致祥在《分段(片)函数的初等性》[4]中就给出了如下定理:
定理 1.设 x1刍x2刍…xn+1

若 fk(x)是区间[xk,xk+1](k=1,2…n-1)上的初等函数,且

则 f(x)是区间[x1,xn+1]上的初等函数。 并且(3)可以等价地表示为

在此需要强调的是,对这个定理的证明(略)也是采用把f(x)“用一个式子表示”的方式。
从以上举例来看,首先,(1)、(3)式分别和(2)、(4)式相比较,(2)和(4)式不但是“由基本初等函数经过有限次的四则运算与复合运算所得到的函数”,而且它们还分别互相等价地表示。 即便如此,(2)和(4)式却构造了形如式子,这样的式子直接违背了数学形式或结果必须化简的简洁性之原则,因此,作为一个数学学者,即使是牺牲这类分段函数是初等函数的可能,也不应鼓励这类把结果或形式复杂化的逆数学原则之构造。
其次,这类构造并不能解决像

这一类分段函数是不是初等函数的问题,特别地,在什么是初等函数的问题上,如果承认分段函数只要“可用一个式子表示”就是初等函数,那么,一个令人头疼的问题是:现在人们还不能把符号函数“可用一个式子表示”,随着数学的深入发展,将来是不是有可能“用一个(更为复杂的、人们现在还想不到的)式子表示”呢?例如高斯函数y=[x],就有学者把它表示为:

如此,把一个简单明了的取整函数表示为复杂到必须耐心计算才能看懂的函数形式——其目的仅仅是为了验证它是不是初等函数,这是不是在打开潘朵拉魔盒呢?我想,这是任何数学达人也不愿意看到的徒劳无功的努力。
再者,若把“分段函数是否是非初等函数”的问题看作是分类问题,那么,关键是看分类的方法是否简单可行。如果把形式简洁的分段函数用能否构造一个必然是复杂的 “用一个式子表示”的函数形式来作为判断的方法,这种把简单问题复杂化的分类的方法不仅不利于教学,也无利于对分段函数的研究。
最后,我们判断分段函数是否是初等函数的目的就是为了利用初等函数所具有的良好性质(如连续、可导、可积等性质)。从这一点上来说,数学教育工作者对分段函数是否初等函数的问题的思考,并提出构造性的解决方案,是值得尊重的。但需要商榷的问题是:“分段函数是否是初等函数”的问题明显地是由初等函数的定义不严密、甚至是理论缺陷所造成的,为什么不是采取修订定义的方式、而是继续在不严密的定义的基础上来探究其所遗留的的问题呢?例如,历史上的函数极限的定义,还有数学(概念)公理化运动,都是由不严密逐渐走向严密定义来解决其中的问题的。因此,笔者不敢苟同这种亡羊不补牢、反而去追羊的非数学的解决问题的方式。
总之,笔者反对把(部分的)分段函数是否能够“用一个式子表示”来证明它是初等函数的解决问题的方式,而是坚持主张“凡是分段函数都是非初等函数”这一简明扼要的结论。可是,怎么严密初等函数的定义来杜绝这一问题呢?其实,针对这一问题只需要把定义2里的“可用一个式子表示”修正为“用一个最简化的式子表示”,就杜绝了任何企图把已经是最简化了的分段函数的不同分支的函数形式再简化为 “用一个最简化的式子表示”的可能。例如形如式子的最简式子只能是或只能分段表示,这样就杜绝了构造(2)、(4)的任何努力,当然也排除了(6)的合法性。我认为,这才是樊映川和同济大学高等数学教材编写组等前贤们为什么要增加“用一个式子表示”的真实意图的表达。
现在遗留的问题是,若肯定“凡是分段函数都是非初等函数”,那么,由于整个数学分析或高等数学都是以初等函数为基础对象展开研究的,我们就无法利用初等函数的良好性质、甚至是方法来研究分段函数了。为了解决这个问题,就要先解决初等函数的定义所存在的理论缺陷。
2.初等函数定义的理论缺陷
我们知道,在研究函数的过程中,会经常碰到像y=sinx,x∈[-1,1]、y=,0燮x燮1等这类函数。它们既不是经过有限次四则运算、也不是经过有限次复合运算所得到的,若直接根据初等函数的定义来判断,那么,这类函数就不能被称做是初等函数;另外,即使把y=sinx,x∈[-1,1]和其被改变的母函数y=sinx,x∈(-∞,+∞)相比较,它们虽然具有同一个解析式,但由于定义域不同,所以,它们不是同一个函数,因此,我们不能因为y=sinx,x∈(-∞,+∞) 是 (基本) 初等函数就认为y=sinx,x∈[-1,1]也是初等函数,数学也不允许这种类比推理。
可是,这类函数是初等函数毕竟是公理性常识,例如,在定理 1 中就有“若 fk(x)是区间[xk,xk+1](k=1,2…n-1)上的初等函数”;还有高等数学教材中,求分段函数的某一分支函数的极限、导数、积分时,我们也都是按照初等函数来处理的。因此,这类函数是否是初等函数若不能从初等函数的定义中直接或间接地推导出来,那么,必须、也只有直接定义它们是初等函数,即,给数学概念下定义的目的就是确立人们在数学上所认识的公理性常识;换句话说,初等函数并不仅是“由基本初等函数经过有限次的四则运算与复合运算”这一途径得到,还可以通过改变(基本)初等函数的定义域而得到。因此,若在给初等函数下定义时漏掉了这一途径所得到的函数,那么,只能说明初等函数的定义存在着理论上的缺陷。
综上所述,初等函数的定义应当修订如下:
定义3:“由基本初等函数经过有限次的四则运算和有限次的函数复合步骤构造并用一个最简化的式子表示、或改变其定义域所得到的函数,叫做初等函数。”
关于定义3需要说明如下两点:第一,定义2表述为“由常数和基本初等函数……”是不准确的,这是因为,在函数的解析式中所含常数,对于任意一个x,都与这个常数相对应,所以,常数在函数解析式中是以函数面目出现的,即为常数函数,因此,不能把常数(函数)排除在基本初等函数之外。相比较而言,定义1把常数(函数)作为基本初等函数的一种,是比较恰当的,总之,定义3中的基本初等函数是指常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数等六种函数;第二,定义3确定了只改变初等函数的定义域所得到的函数仍为初等函数,这个定义对于大多数分段函数来说,即使整体上不是初等函数,但只要其分支是初等函数,像函数的连续、可导、可积等这些本来就是函数的局部性质和运算在其分支上依然可以成立和进行。这实际上意味着,分段函数即使不是初等函数,若它的分支函数是初等函数,那么就不会影响对它的研究;另外,在深层次上,把分段函数的问题化整为零来处理,正是微积分思想和方法的精髓。从这一点上来说,把分段函数归类于非初等函数,不仅便利于教学,也易于培养学生数学地分析问题、解决问题的思想和方法。
[1]华东师范大学数学系.数学分析(第三版)[M].北京:高等教育出版社,2001.
[2]同济大学应用数学系.高等数学(第五版)[M].北京:高等教育出版社,2005.
[3]匡继昌.什么是初等函数[J].数学通报,2007,(7):27.
[4]刘文,刘致祥.分段(片)函数的初等性[J].河北工学院学报,1989,(1):19.
[5]付有祥,伏文文.基本初等函数表示高斯函数的思维过程分析[J].佳木斯教育学院学报,2010,(6):62.

