一种改进型遗传算法的网格工作流调度研究
赵 斌,宿玉佩,蒋念平
(1.洛阳师范学院计算机系,河南洛阳471022;2.重庆医科大学附属第一医院,重庆400016;3.上海理工大学光电信息与计算机工程学院,上海200093)
0 前言
网格技术是互联网计算技术的一个重要发展方向。作为网格计算的重要部分,借助于工作流技术,人们提出用网格工作流来解决网格环境方面遇到的问题。
网格工作流是多项网格服务的综合。这些网格服务以一种预设顺序分布在各种分布式网格节点予以执行,以最终完成一项具体任务。任务调度是网格工作流研究方面的一个重要话题,与一般的任务调度不同,网格工作流调度必须考虑的是不仅要为任务选择最优资源,而且还需考虑各任务之间的用时或因果约束条件。任务与各节点之间的映射关系由此构成网格工作流调度方案。
目前,网格任务调度集中在改进调度算法上。而Globus网格环境主要处理标识问题与资源发现,对任务调度与提交算法都不很完善。任务调度采用轮循方法,任务提交采用命令行方式,容错性差,对负载平衡没有考虑。如Min-Min等是比较老的算法,一般网格任务调度算法多数是与这些算法相比较。但根据网格计算任务调度系统的特点,这些传统调度算法不能很好的适应网格资源的要求。高效任务调度算法可提高整个计算网格计算效率,但网格计算系统中某资源出现故障可能性较高,系统资源会不断增长,系统性能和结构会不断发生变化,这就要求资源管理程序能很好的动态监视与管理网格资源,从可利用资源中选取最佳资源服务,减小这种故障或失败、整体结构和性能发生变化等问题对网格整体性能的影响[1-2]。
本文提出一种基于改进型遗传算法的资源调度算法。为了避免收敛速度过慢且不那么容易局限在局部最小范围内,该算法增加了二级优先杂交和二级优先变异运算,表现出良好的收敛特性和效率。
1 问题描述
网格工作流建模允许网格工作流任务或工作量操作根据他们之间命令的执行情况建立相应模型。把实际问题通过建模语言转化成对应的任务序列,再通过任务序列之间的关系进一步转化成对编程语言的描述[3]。本文的网格工作流模型是基于有向无环图(DAG)模型而创建的。图1给出了一个由有向无环图来表示的网格工作流。DAG工作流模型将工作流描述成一系列的子任务。子任务之间的依赖关系和优先关系构成一个有向无环图G=(V,E,W),其中,V代表图中的所有节点,即工作流的所有子任务;E是图的有向边,即各任务之间的依赖关系和优先关系;W是有向边的权重,即任务Vi所需的执行成本。
运行时间最长的路径是关键性路径。在图1中将最大的Σ W设为关键路径,并选择(V1→V3→V5→V6)为关键路径,(V1→V2→V4→V6)为非关键路径。这样一来,关键路径上就存在子任务((V1→V3),(V3→V5),(V5→ V6)),非关键路径上就存在((V1→ V2),(V2→V4),(V4→V6))。然后,将快速运行的资源配置给关键路径上的各任务,将成本低的资源配置给非关键路径上的各任务[4],因此,网格工作流任务调度的总计算成本得以降低。
工作流调度的本质在于将关键路径或非关键路径上合适的子任务分配给一个特定的网格资源以执行操作,使得整个任务的计算成本总数控制在最低。
假设有 n 个子任务 Ti=(i=1,2,3,…,n)和 m 个可用网格资源 Rj=(j=1,2,3,…,m)。根据任务之间的优先关系和约束关系,工作流调度将n个子任务分配给m个可用网格资源以充分利用它们。Ci是完成工作Ti所需的用时。调度的目标在于使Σ Ci控制在最低,从而降低计算成本。
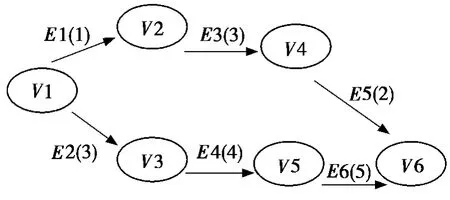
图1 基于DAG的工作流模型
2 改进型算法
任务调度问题是一个典型的NP-完全问题。如果应用标准的遗传算法来进行调度,存在两大缺陷:(1)容易陷入局部最优解;(2)收敛速度慢。鉴于此,本文对传统的遗传算法做了改进。新算法对自然数进行编码,并增加了二级优先杂交和二级优先变异过程,然后保留每一代的最优个体,从而有效地保障了全局搜索和局部搜索的强大性能。
2.1 代码设计
为了比二进制编码的染色体更能维持物种的多样性,同时使得编码和解码过程简单化,新算法对带有自然数的染色体进行编码[5]。
染色体的长度等于分配任务的个数,用Y=(X1,X2,X3,…,Xi,…,Xn)来表示一条染色体。每条染色体的每个节点可以表示为一个二元Xi(Si,pi)(i=1,2,…,n),Si是分配到任务i的资源,任务个数i是唯一的,每项任务获取到一个资源,不同的任务可以获取到相同的资源;pi是该任务的优先值。
为了改善个体库存的覆盖数,采取随机初始化方法,即随机选择一个资源来运行任务i。
2.2 适应度函数
适应度函数用来评估当前染色体的适应能力,它可以有效地反映每条染色体与最优解染色体之间的差距。适应度函数的值对问题的解决起着决定性的作用。建立预测值Value=[Ti,Rj]的二维列阵,其中,Ti是任务i;Rj是资源j。通过获悉Ti的分配任务和Rj的计算能力之间的关系可以计算出相应的理论期望值。本文中的适应度函数取决于所有任务的调度的预计完成用时。将这个预计完成用时的倒计时视为评估条件,即

式(1)是染色体的适应度评估,其中,n是染色体的长度;Yi是i-位染色体对应资源的值。如果适应度越大,表明染色体更优越,反之,就越低劣。
2.3 选择
选择算子决定的是哪些染色体可以保留到下一代。本文应用轮盘赌法来进行选择。轮盘赌法选择的目的在于将集合中的元素映射到一个范围内。然后分成多个子分段(每个分段对应一个元素),由此便会出现n个有效随机个数,统计好每个频率出现的随机个数,然后选出出现频率最高的那个分段的元素[6]。
该算法基于染色体的适应度值来决定所选染色体的概率。如果染色体的适应度值较大,那么被选中的概率也就大。为了实现轮盘赌选择,每轮会生成[0,1]范围内的随机数字,以作为参考概率。被选个体ri的概率表示为

其中,pSize是种群的大小。
每条染色体被选的概率决定好后,将参考概率与选择概率进行对照,如果前者大于后者,该染色体就入选;否则,就放弃。
2.4 交叉运算
交叉运算可以改变两个父代个体的部分结构并将它们组合成一个新个体。新个体遗传这两个个体的特征。此时,问题变成了寻找最优方向。在这一算法里,为确保种群的多样性,交叉会出现在随机位置,随后就需要对新个体的适应度值进行评估。根据评估结果,算法会进行合理调整。为了提高解空间的收敛速度,二级优先杂交只会发生在适应度值低于平均适应度值的个体和种群的最优个体方面。交叉概率是Rs,通常为0.4~0.9,随机挑选两个个体,生成随机个数r[7]。
2.5 变异运算
通过变异,可以稍微改变染色体被选中的概率,从而保障染色体的多样性,判定遗传算法的局部搜索能力。
该算法存在变异概率很小的染色体,然后需要对新个体进行适应度值评估。该算法基于评估结果进行二级优先变异。为了维持染色体的多样性、改善最优生成能力,单点变异只发生在适应度值小于平均值的个体和种群的最优个体方面。变异概率Rc,通常为0.001~0.100[8],获取新个体。
2.6 保留全局最优个体
每一代繁殖结束后,就获取到当前的最优个体,是一个近似最优解。然后比较当前生成的最优个体与全局最优个体的适应度值。如果前者大于后者,就替换掉全局的最优个体;否则维持不变。这个生成的个体如果符合替换条件,就停止繁殖,否则继续繁殖。
通过上述步骤,可以判断模块之间的运算关系并采用流程图来表示。改进型算法的运算过程如图2所示。
3 研究结果
本文使用Gridsim[9]工具在异构网格环境下进行模拟试验。Gridsim为网格有效资源分配技术提供模拟环境。它是网格计算平台,它能够模拟异构、进行简单的网络任务的虚拟处理等。
在应用改进遗传算法前,先对遗传算法参数进行配置,如种群大小,交叉与变异概率设置。试验初始种群为100。可发现交叉概率取0.74~0.76时,适应度函数较稳定且最优[10],如图3所示。
对改进型遗传算法和标准遗传算法进行分析后再作比较。有关模拟参数有:机器、处理元素和每秒百万指令。所以本论文中主要参数是:种群大小100、种群迭代次数50、交叉概率0.80、变异概率0.01。仿真结果如图4和图5所示。图4是不同任务在100种资源之间调度的结果。图5是100个任务在不同资源之间调度的结果。每个坐标点的值即是当前连续10次调度的平均值。
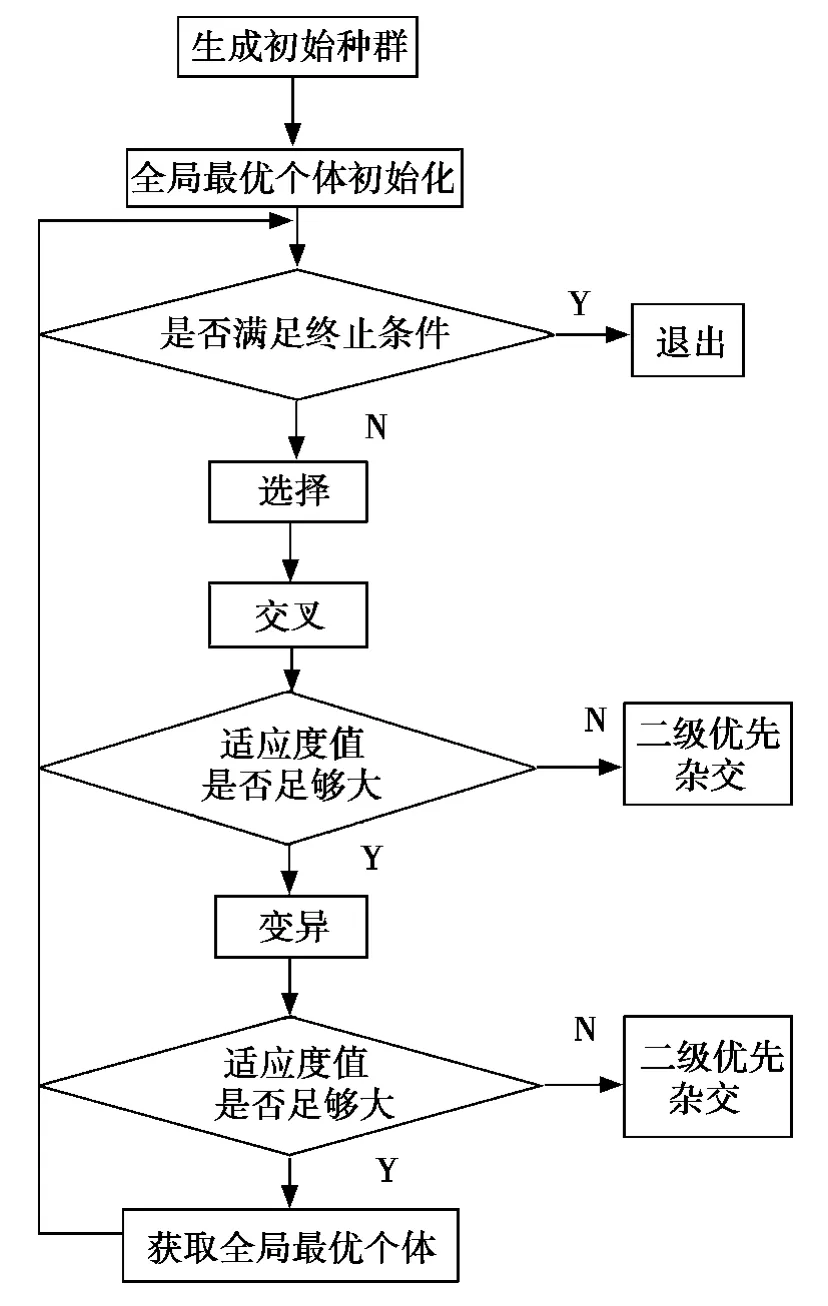
图2 改进型遗传算法的操作过程
图4 是在保持网格资源个数不变的情况下,通过改变任务的个数而进行的模拟试验。通过对比两组试验数据,可知改进型遗传算法的完成用时比标准遗传算法的少,且成本也低。图5是在保持任务个数不变的情况下通过改变网格资源的个数而进行的模拟试验。通过对比两组试验数据,可知改进型遗传算法的完成用时比标准遗传算法的少,且成本也低。
通过对两种情况的仿真试验结果相比较可得出:改进后遗传算法网格工作流调度算法与传统遗传算法的网格工作流调度算法相比,具有更好的寻优能力,在全局收敛方面显示出了良好的性能。改进后调度算法能够缩短整个任务的总体执行时间,并且在大规模网格工作流调度环境下得到了较好的性能和效果,能够在实际网格中加以应用。
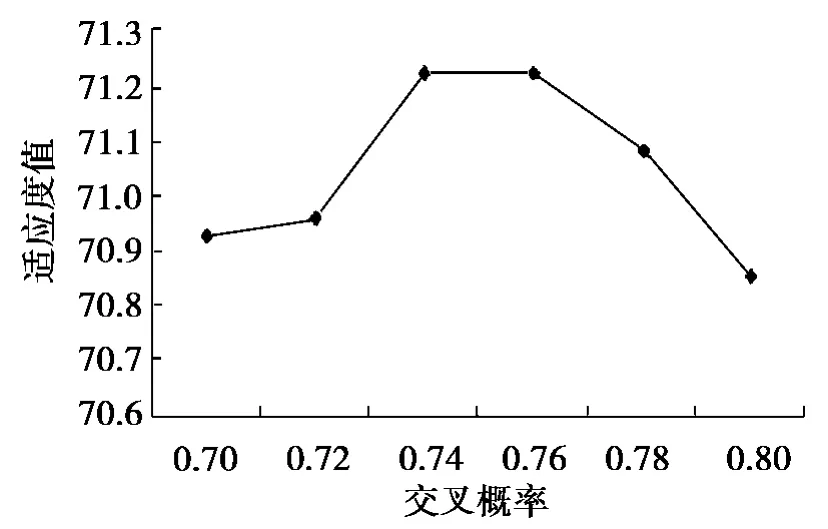
图3 遗传算法的交叉概率效果
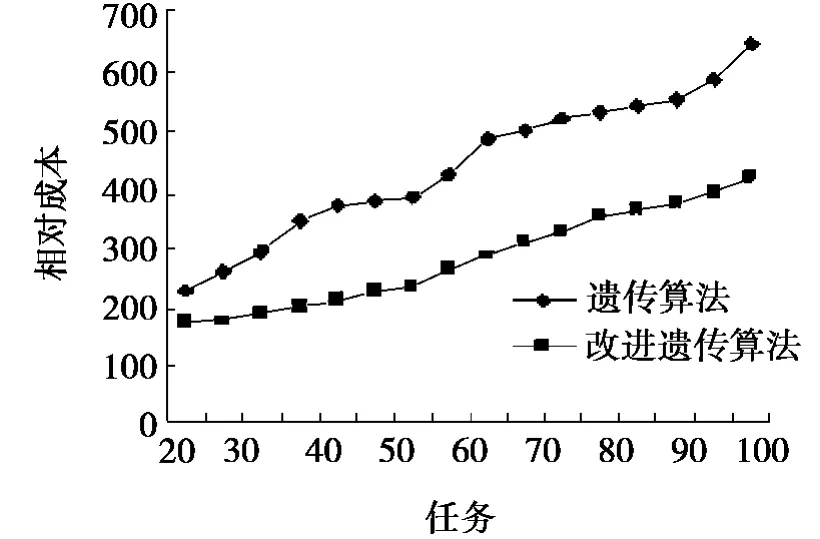
图4 不同任务在100种资源之间的调度
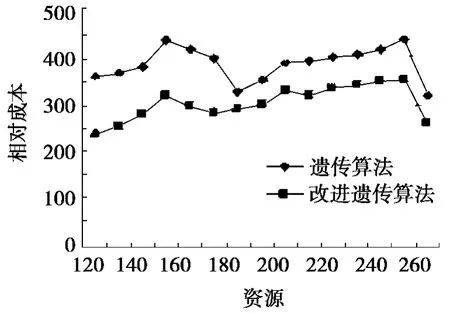
图5 100个任务在不同资源之间的调度
4 结论
基于二级优先杂交和二级优先变异,本文提出了改进型的遗传算法,结果表明:该算法在维持种群多样性的情况下具有良好的效率和收敛性,能够更有效地解决网格工作流调度问题。最终,通过模拟试验,证实该法比标准的GA算法更有效。当然,这方面的研究还存在诸多问题需要深入探讨,例如,如何解决网格工作流的工作量的平衡问题。
[1]吴高锋,蒋玉明.基于QoS改进的Min-Min网格调度算法[J].微计算机信息,2009,9(3):110-112.
[2]叶春晓,陆杰.基于改进遗传算法的网格任务调度研究[J].计算机科学,2010,37(7):233-235.
[3]Jia Y,Rajkumar B.A Novel Architecture for Realizing Grid Workflow Using Tuple Spaces[C]//Fifth IEEE/ACM International Workshop on Grid Computing IEEE.2004:119-128.
[4]Fen H,Wang L,Yang H.Grid Workflow Technology and Its Application in Teacher Professional Development[J].Audio-Visual Education Research,2007,5(2):32-35.
[5]Yuan Y C,Li X P,Wan Q,et al.Bottom Level Based Heuristic for Workflow Scheduling in Grids[J].Computers,2008,2(5):67-70.
[6]Srinivas M,Patnaik L M.Genetic Algorithms:Asurvey[C]//IEEE Comput.1994:17-26.
[7]Wang X P,Cao L M.Genetic Algorithm[M].Xi’an:Xi’an Jiaotong University Press,2002.
[8]Wu X Q,Zeng W H.Grid Resource Scheduling Algorithm Based on Improved Genetic Algorithm[J].Microelectronics and Computer,2006,23(9):26-29.
[9]Anthony S,Chen S Y,Rajkumar B.Visual Model for Grid Modeling and Simulation(GridSim)Toolkit[C]//ICCS.2003:1123-1132.
[10]陆杰.基于遗传算法的网格任务调度研究[D].重庆:重庆大学,2010.

