公务员考试中数字推理题全是错题

刘国祥

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

公务员考试中数字推理题全是错题

刘国祥

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

历年的全国及地方公务员考试中，数字推理部分的“找规律，填数字”类题目是必考题，用Lagrange插值多项式看，全是错题.并且呼吁有关部门立刻停止使用或者修改这类试题.

数列；递推数列；Lagrange插值多项式

历年的全国及地方公务员考试中，数字推理部分的“找规律，填数字”类题目是必考题，并且占分比例不小，与参加过考试或者备考的考生交流，认为这类题目难度大，在短时间内不容易发现“规律”.因而，有人专门研究过解题策略.用Lagrange插值多项式角度看，全是错题.

如：2010年国家公务员考试行政能力测试中的“数字推理”部分试题.

给你一个数列，但其中缺少一项，要求你仔细观察数列的排列规律，然后从四个供选择的选项中选择你认为最合理的一项，来填补空缺项，使之符合原数列的排列规律.

考试部门给出的“标准”答案分别是C，D，B，A，B.

这类题目，从小学到中学，以至于大学，学生都没少练习过（但是不一定考试，最起码比较重要的考试，如高考，研究生入学考试从未考过），它对于培养学生认真观察、归纳总结、合情推理等方面能力，考查解题的敏捷性，思维的发散性等方面的素质都有好处.历年的全国及地方公务员考试中，这类题目是必考题.

除了难易有别外，这类题目都是通过给出数列的几项，要求你发现或者总结规律，根据规律，确定空缺处的项.公务员考试中，题目的叙述非常“温馨”，但是题目确是错误的.

众所周知的是，归纳法有完全归纳和不完全归纳两种，不完全归纳法是发现新规律的有效方法，但是得到的结论不一定正确.“找规律，填数字”显然是不完全归纳，从不同的角度观察，可以得到不同的规律.也就是说，“规律”不唯一.那么，这种题目的解具有多样性甚至是任意性.

先看一个简单题目：

例 1，2，3，（ ）.

作为填空题，空白处容易想到填4可以，这是“正整数从小到大的排列”的规律.如果想到卢卡斯数列（斐波那契数列的变形），“后一项是它前面两项的和”，空白处填5.这两个“规律”都容易发现.从不同的角度考虑，可以得到不同的结果，作为填空题，考查学生的思维发散性，答案不唯一，不能说不可以.

但是象公务员考试一样作为四（多）选一选择题，如备选项是：

A.4 B.5 C.6 D.7.

那么，选A或者B都不错误.“你认为最合理的一项”，不同的人可以有不同的“认为”.你可能说，备选项设置不合理，不妨改为：

A.4 B.15 C.26 D.37.

那么，选择B、C、D都不错误.

下面应用Lagrange插值多项式来给出这类题目的“一般性”解答.

对于一个数列，已知a1,a2,a3,……,am，求am+1.这是例题以及41，43,44,45题目的类型.

对于一个数列，已知 a1,a2,a3,…,ak-1,ak+1,…,am，求 ak.这是例题以及42题目的类型.

结论：对于以上两类题目，答案可以是任何数（包括复数）.

就以第一类为例，另一类同样适用.

用函数记f(n)=an,n=1,2,3,……,m,m+1，那么，这个合理的选项就是f(m+1).

设给出的m个点(n,f(n)),n=1,2,3,……,m,m+1在m次多项式的图像上.那么这个多项式用Lagrange插值多项式来表示就是：

如果设f(m+1)=t.t是任意数（包括复数），那么f(m+1)=p(m+1)=t.

就以最简单的例来说，xi=i,f(xi)=i,i=1,2,3.

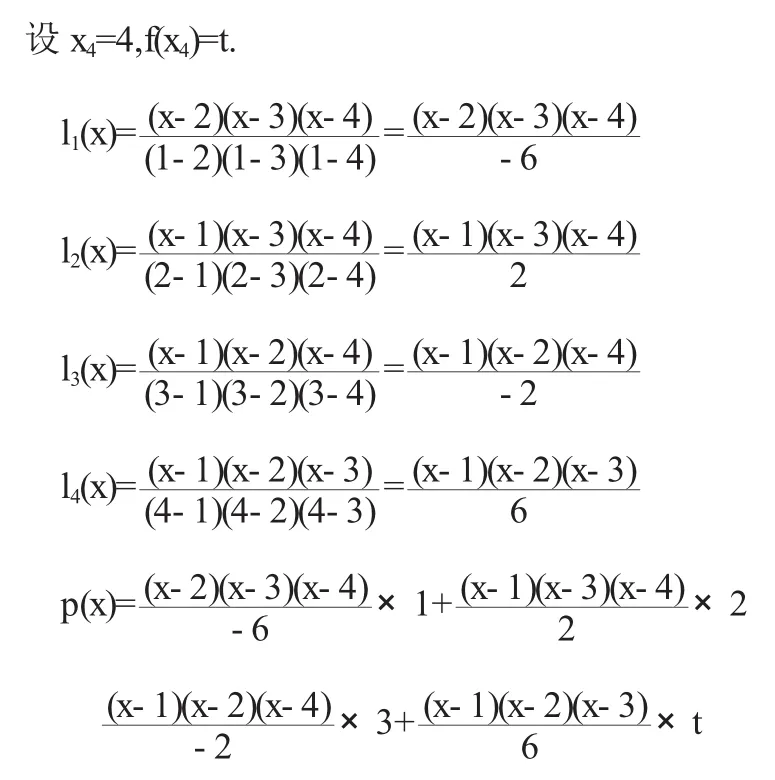
这就是一个规律.也就是

而f(i)=p(i)=i,i=1,2,3.

分别取t=4,15,26,37.都有f(i)=p(i)=i,i=1,2,3.而f(4)=p(4)=t（4,15,26,37）

再考虑稍难点的的44题.

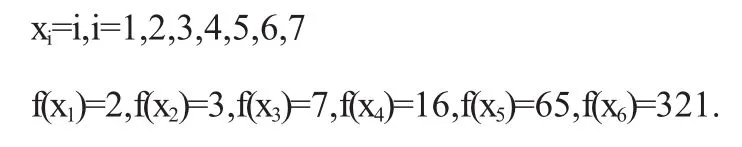
记f(x7)=t.则

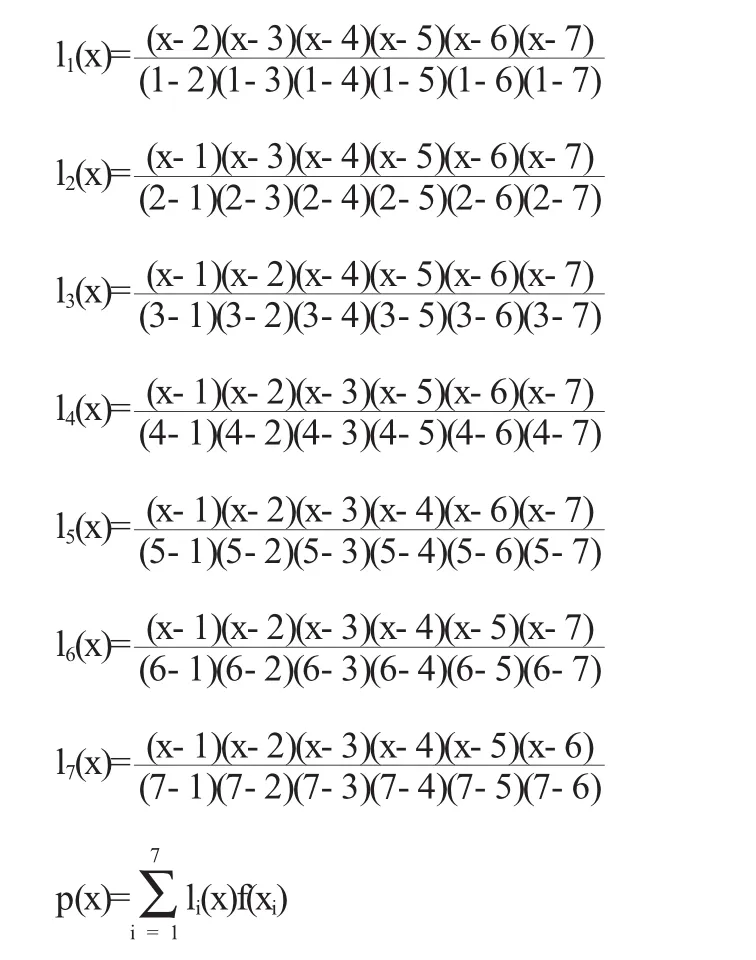
不化简，更容易看出：f(i)=p(i)=i,i=1,2,3,4,5,6,7.

而由于f(x7)=t.t的任意性.已得到任意值.

分别取t=4546,4548,4542,4544.就分别得到四个选择项的值.

或许有人感到构造Lagrange插值多项式不容易，那么，观察出“规律”就容易吗？例如考试部门给出的标准答案也不易.

公务员考试是国家最重要的考试之一，有人称为“国考”，但是这样的错误题目使用多年，造成的不公或危害不可估量.呼吁有关部门立刻停止使用或者修改这类试题.

〔1〕关冶，陆金甫.数值分析基础[M].北京：高等教育出版社，2005.

〔2〕中华人民共和国劳动人事部.2010年国家公务员考试行政能力测试试题.

O174.42

A

1673-260X（2012）02-0020-02