创建数学模型探究汽缸节能优化方案

史秀英

（赤峰学院 成人教育学院，内蒙古 赤峰 024000）

创建数学模型探究汽缸节能优化方案

史秀英

（赤峰学院 成人教育学院，内蒙古 赤峰 024000）

本文采用几何画板建立数学模型，定量地分析了在曲柄连杆结构偏置时的受力和能量转化情况，得到了内燃机活塞摩擦功耗显著减少的结论，摩擦力的减少导致内燃机机械效率增加.

几何画板；曲柄连杆结构；偏置距离；摩擦功耗；机械效率

本文采用几何画板建立数学模型，定量地分析了在曲柄连杆结构偏置时的受力和能量转化情况，得到了内燃机活塞摩擦功耗显著减少的结论，摩擦力的减少导致内燃机机械效率增加.它对提倡节能减排，具有积极的现实意义.

1 问题提出背景

汽车改变了人类的生活.我们通过用数学与物理应用软件《几何画板》模拟汽车内燃机的工作过程，了解到内燃机摩擦消耗的能量约占总功率的30%以上，活塞与汽缸壁间的摩擦力与活塞对汽缸壁的正压力成正比，这个正压力主要来自活塞和连杆之间作用力的在活塞运动方向相垂直的分量.活塞和连杆之间的作用力在做功冲程中的值远远大于在压缩冲程中的值，这是一种受力的不对称.而现有的内燃机结构在压缩冲程和做功冲程中曲柄连杆结构是对称的（点A与点C始终在一条直线上）（图1），从资料中了解到有将连杆偏置（点A与点C的轨迹不在一条直线上）式的内燃机，分析该类机型后对比普通机型我们就提出了一个猜想：这种发动机可以使得做功过程得到优化，我们借助《几何画板》建立数学模型，发现当活塞与汽缸中心连线远离曲轴中心(偏置)0.71厘米的时候(图2)内燃机输出功增加了1.5%,具体的研究过程总结如下.

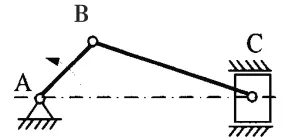
图1 H=0普通内燃机曲柄滑块机构

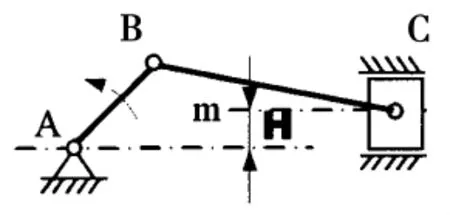
图2 H：偏置式曲柄滑块的偏置距离

2 内燃机的工作过程

为了研究方便我们引入几个术语(见图3,图3是汽车内燃机工作原理图）：

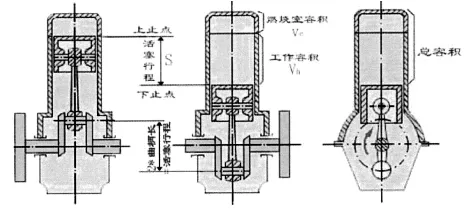
图3

(1)上止点——活塞顶面位移到距离曲轴中心线最远时的位置.

(2)下止点——活塞顶面位移到距离曲轴中心线最近时的位置.

(3)活塞冲程——活塞的上止点与下止点间的距离.

(4)活塞在某一时刻的气缸容积——活塞在某一时刻时汽缸中气体的体积,单位为升.

图4

图5

内燃机有四个冲程：进气行程(图4)、压缩行程(图 5)、做功行程(图 6)、排气行程(图 7).

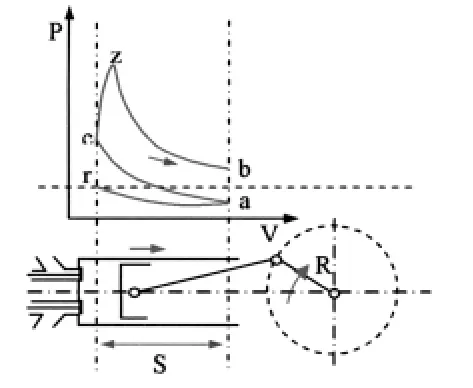
图6

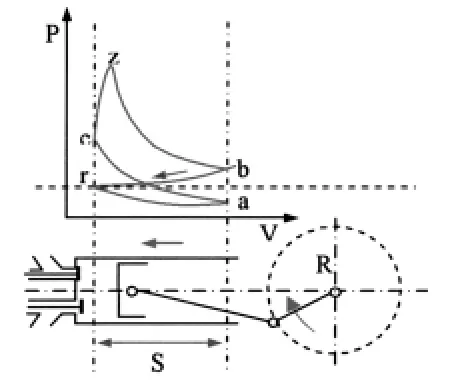
图7

即四冲程汽油内燃机经过进气、压缩、做功、排气四个冲程完成一个工作循环，这期间活塞在上、下止点间往复运动了四个冲程，相应地曲轴旋转了两圈.

3 借助《几何画板》创建数学模型

接下来我们运用《几何画板》软件平台，建立数学模型.

3.1 创建活塞压力计算数学模型

从《汽车常识》中得到根据压强体积曲线（横轴表示：活塞在某一时刻的气缸容积，纵轴表示：活塞所受的压强）我们可以作为后面几何画板建立数学模型的依据，（如图8）.

经分析可知在压缩冲程中有一个阶段气缸内大气压小于外界大气压，真实的内燃机在吸气冲程和排气冲程中气缸是与外界连通的，活塞受到的压力极小，气压大致与标准大气压一致，在做功阶段气缸内压强远远大于外界大气压，因而只许分析做功冲程与压缩冲程中的压力情况即可.

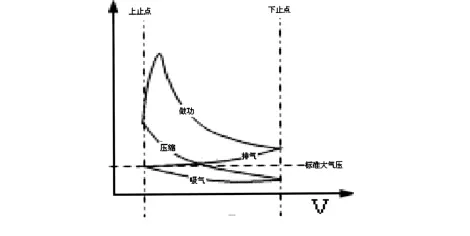
图8 内燃机的PV曲线

在几何画板中，得出发动机中每个环节中实际压力的大小比较困难，为了理解方便又不至于影响研究问题，我利用假设的方法假设汽缸活塞所受到的力的情况由（图9）中所标数据所示（横轴表示：活塞离开曲轴中心的距与活塞横截面积的积所形成的体积，纵轴表示：活塞所受到的压强）并用一系列的线段来拟合压强曲线，曲线LO代表做功冲程中的压强曲线，曲线JG代表的是压缩冲程中的压强曲线，左右两边竖线分别是下止点与上止点的位置，规定下止点距曲轴中心的距离为12.6cm，上止点距曲轴中心的距离为33.5cm，取活塞的横截面积为1个面积单位，若将体积单位以升记，活塞的横截面积为1平方分米，则“体积压强”曲线可以当作“距离压力”曲线使用（图9）.

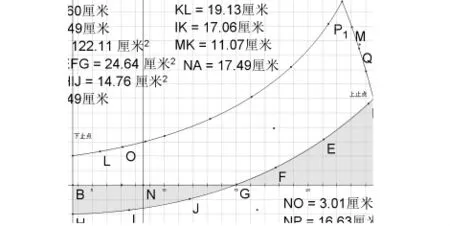
图9

3.2 创建偏置曲柄连杆结构数学模型

首先引入一个定义

定义1：偏置距离H是指活塞与汽缸中心连线离开曲轴中心的距离.

其次给出一些变量

H：偏置距离，变量

xmax：上止点活塞位置（上止点离开曲轴中心的距离），定值33.5cm

xmin：下止点活塞位置（下止点离开曲轴中心的距离），定值12.6cm

R：曲柄长度，随H变化的变量，为了保持固定的气缸工作容积

L：连杆长度，随H变化的变量，为了保持固定的气缸工作容积

在下止点xmin时，有如下几何关系xmin2=(L-R)2-H2如（图 10）

图10 下止点几何关系

在上止点xmax时，有如下几何关系xmax2=(L+R)2-H2

解得：

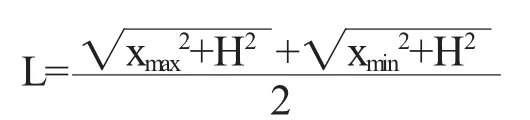
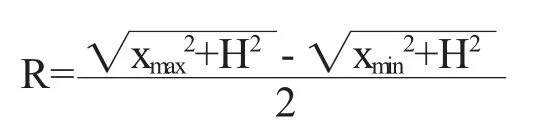
这样通过调整L和R的长度保证固定的上止点和下止点活塞位置，保证在不同偏置位置的时候，具有相同的汽缸体积，这样就保证了做功冲程和压缩冲程的气压在不同偏置情形下保持一致.

将曲柄与x轴正方向之间的夹角α定义为一个参数，对于α的每一个值，当曲柄处在某个位置R处，活塞S点的位置一定在以R点为圆心，以L为半径的圆与活塞轨迹相交的交点上，这样确定了活塞的位置，使得当R旋转的时候，活塞S随之水平移动，连杆角度也随之变化.由此用几何画板建立了曲柄连杆结构在偏置距离为H状态下的数学模型（图 11）.

图11 建立曲轴连杆模型

3.3 创建活塞受力分析模型

在活塞的受力分析中，可以将活塞运动的每一瞬间近似地看作受力平衡状态.力的方向取向右、向上为正，角度从水平向右逆时针旋转为正.在水平方向连杆与活塞的作用力的水平分量与活塞摩擦力和汽缸内气体对活塞的压力相平衡.在竖直方向连杆与活塞的作用力的竖直分量与汽缸对活塞的约束力相平衡.

F：气体对活塞的压力，根据压力曲线己知

T：连杆对活塞的作用力，未知

N：汽缸对活塞的约束力，未知

f：汽缸与活塞间的摩擦力，未知

活塞与汽缸的动摩擦因数为μ，己知（在这里不仿设为0.25）.

在偏置距离H的时候受力分析见（图12），并可列出相应的力学方程，解出压力与摩擦力公式，见（图 13）.

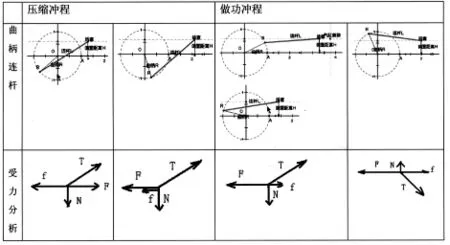
图12

图13

根据图11的模型，可以用几何画板度量出水平向右方向与连杆的角度θ，结合“压力.体积”（图9）与（图13）中求摩擦力的公式可求出各种情况下的摩擦力.

3.4 创建做功分析数学模型

考虑到发动机在实际工作过程中，做功冲程中摩擦力的做功远大于压缩冲程中摩擦力的做功情况，因而我们只对做功冲程中摩擦力的情况进行分析，这不会对得出的结论有大的影响.

用几何画板的度量功能在模型（图11）中度量出角度（水平向右方向与连杆形成的角θ），再用几何画板度量出对应的x值（θ值对应的活塞到曲轴中心的距离），在图9中找出x对应的纵坐标即压力F，由图13三、四列中摩擦力的计算公式算出做功冲程中的摩擦力，由（图12）中的受力分析可知F都是向左的可看成负值，列成下表（图14）.

将图14中的数据描点连线分别得出非偏置（图15）与偏置0.71厘米后（图16）摩擦力距离曲线.

定义2 做功冲程有用功=做功冲程正功-全过程摩擦力负功

由图15与图16不难理解，做功冲程的气缸压力距离曲线与上下止点垂线、水平线围成的面积可以看成压力所做的有用功，使终保持在122.11平方厘米（注：平方厘米不是功的单位，但可以用这一数据描述功的大小，以下类推）.摩擦力所做的功可以看成是摩擦力距离曲线与上下止点垂线、水平线围成的面积.

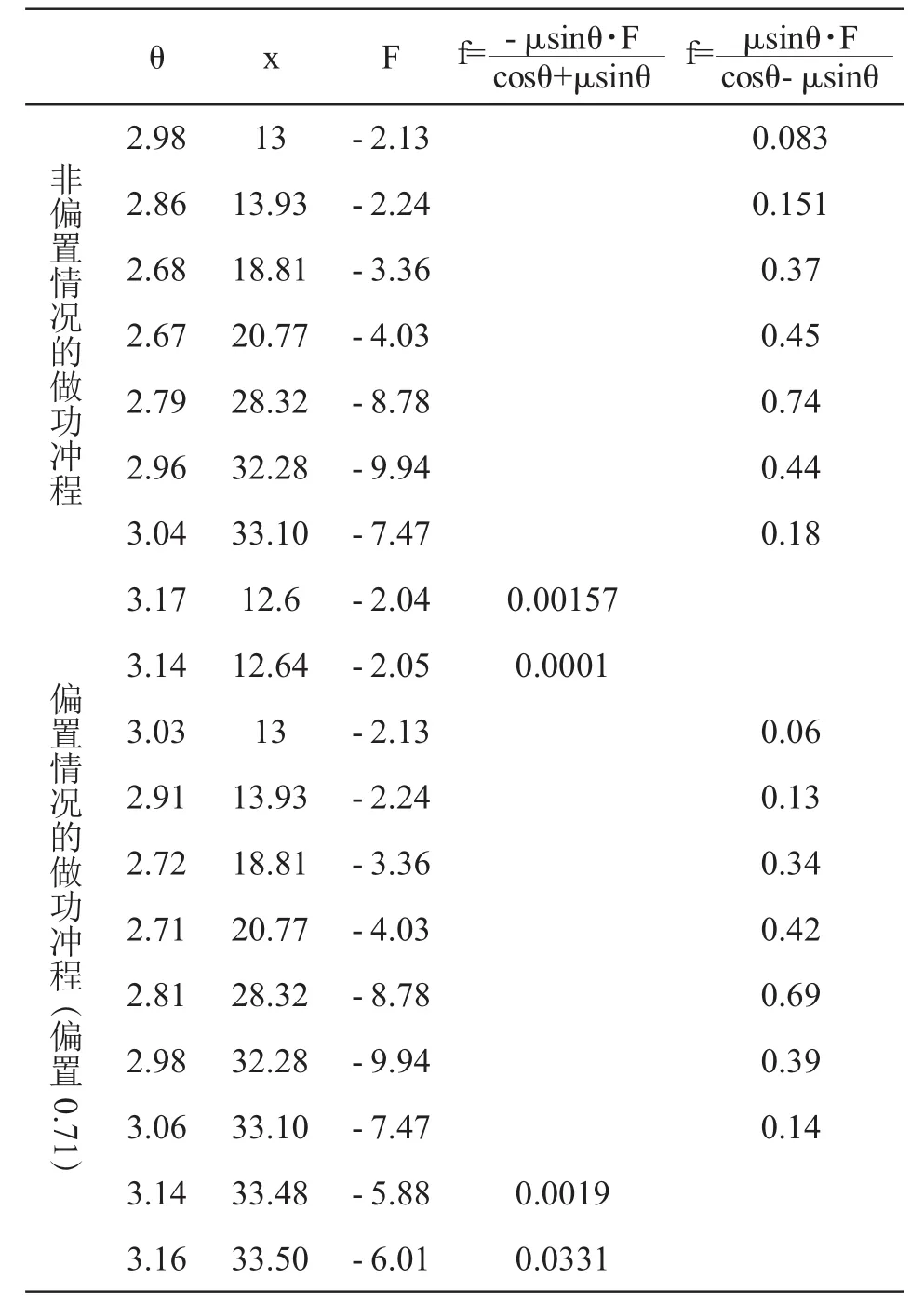
图14

得非偏置状态下有用功：

偏置0.71厘米后的有用功:

可以看出当偏置0.71厘米时摩擦力做功由非偏置的10.89平方厘米减少为9.18平方厘米，度量面积的误差为0.01平方厘米，因此保留两位小数.

图15

图16

输出功在偏置0.71厘米以后增加了1.5%.

〔1〕袁震东.数学建模[M].上海：华东师范大学出版社，1997.

〔2〕赵静，但琦.数学建模与数学实验[M].北京：高等教育出版社，2008.

〔3〕汽车发动机工作原理.http://auto.bowenwang.com.cn/engine4.htm.

O29

A

1673-260X（2012）02-0005-04