统一混沌系统在扩频通信中的研究

苏双臣，庞 晶，2，刘金河，张国勇

（1.河北工业大学 廊坊分校，河北 廊坊 065000；2.北京理工大学 信息电子学院，北京 100081；3.河北工业大学 现代化教育技术中心，天津 300130）

0 引言

所谓混沌同步[1-2]，指的是对于从不同初始条件出发的两个混沌系统，随时间的推移，其轨道逐渐一致.混沌同步是混沌保密通信的关键，所以自混沌理论产生以来，混沌同步就成为广大学者研究的热点.当前，研究混沌新的同步方法不断出现，主要是将其他学科理论和技术引入到混沌同步研究并利用其交叉学科理论和技术改进混沌同步系统的性能如（控制理论与技术）；或是将由研究连续混沌系统转向离散混沌系统最后直至数字[3-4]混沌系统（芯片级混沌电路建立）；或是由低维一般混沌系统转向高维超混沌系统以增加同步系统的复杂性.但针对混沌扩频同步技术研究较少，现有的混沌扩频同步方法大多是单一系统的基于无噪声的仿真，这样大大限制了数字扩频通信的发展.扩频通信另外一个核心的问题是如何产生高质量PN码[5-6].传统的PN序列，如m序列、gold序列等因为其良好的伪随机性、相关性等而广泛应用于扩频通信中，但是，传统的PN序列的复杂度低，数量少，无法满足扩频系统高保密性、大容量等方面的要求.所以基于混沌理论产生的扩频序列具有对初始值非常敏感的特点，若将两个或多个混沌系统进行级联产生的伪随机序列数量众多，并且具有伪随机性和相关特性好、复杂度高等特点.

本文首先构造了统一[7]混沌系统间构成同步系统的通用数学模型，并以lorenz和chen构成的同步系统输出信号作为扩频通信的载波，同时采用串联混沌扩频码logistic-统一混沌系统序列作为PN码，使信息在传输过程中，利用一级混沌产生的序列值，不停的改变次级混沌序列的分形参数[4-6]，从而提高混沌扩频通信的保密性.

1 统一混沌同步系统建立

统一混沌系统是2002年由吕金虎等人提出的一个新的混沌系统[7]，该系统将Lorenz系统、lü系统、Chen系统联系起来，称其为统一混沌系统如方程 (1).

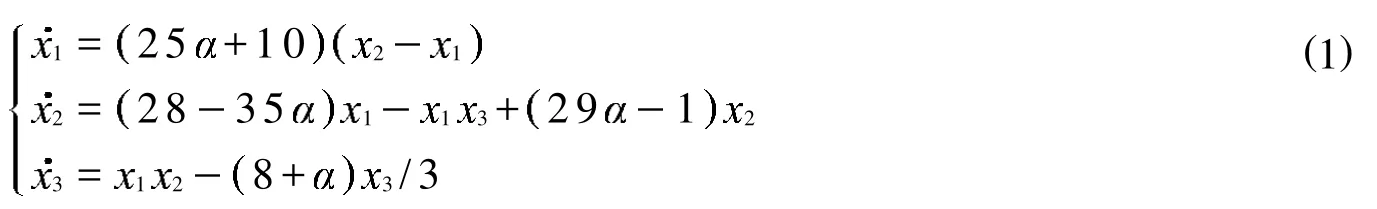
以系统 (1)为驱动方程，以系统 (2)为响应方程构造并证明 (1)和 (2)具有同步性.

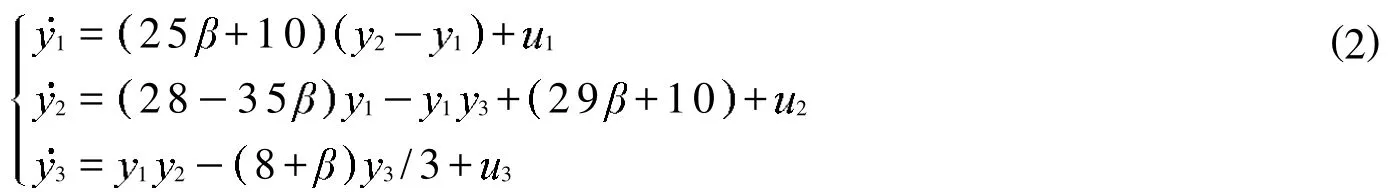
令系统的同步误差动态系统[7]如下

系统误差方程为

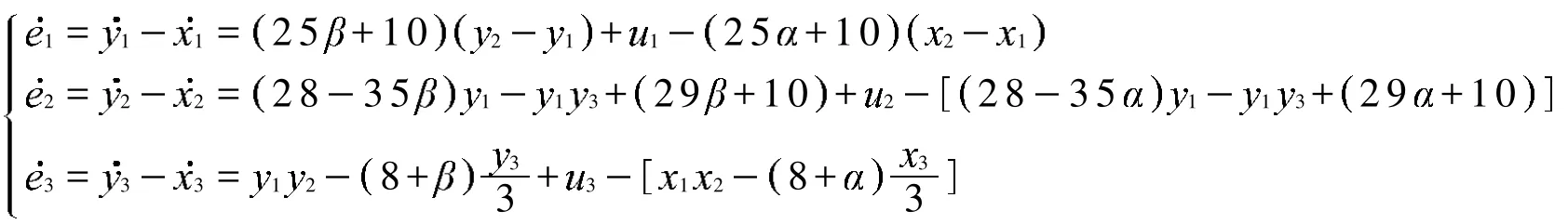
解得

根据Lyapunov稳定定理[9]构造Lyapunov函数

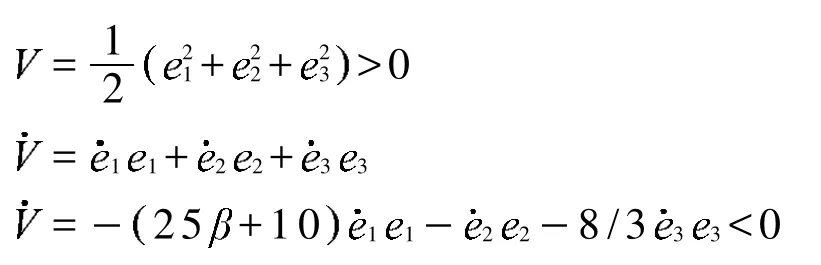
2 同步系统在扩频通信中应用

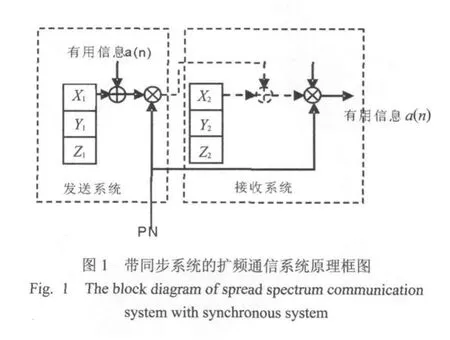
3 级联混沌系统产生PN码

3.1 级联系统的构造

Logistic系统

Logistic-统一混沌系统级联：将logistic的输出值对统一系统参数控制，当Logistic输出值时式 (3)为广义的lorenz系统，时式 (3)为广义的chen系统.随着Logistic（初级系统）伪随机序列在0和1之间随机输出，次级系统形式也发生变化，所以Lorenz系统、chen系统、lü系统也随机出现，这样产生的PN复杂度会更高.

这里存在问题1：logistic是离散序列，而统一系统是连续值，怎样用离散值控制连续值？解决方案是：将统一系统用欧拉法进行离散化，为使离散化的系统保持蝴蝶效应，采样间隔采取0.01 s，同时初级系统（logistic）迭代步长为0.01 s.

这里存在问题2：连续混沌信号通过一定离散化方式，经过截取而获得的混沌序列，这种序列不可能达到理想的自相关和互相关特性，所以当序列长度较短时，这些映射所产生的序列性能会更差，因而有必要再寻找一种在截取有限长度后仍能保持良好特性的混沌序列.解决的方案是：采用多种混沌进行映射级联，级联的混沌产生出的混沌序列要比单级产生的序列要长，且级联的次数越高，则产生的混沌序列的越长.

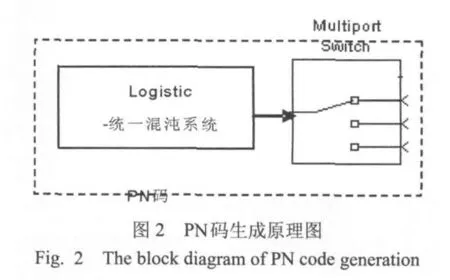
3.2 PN码产生：

3.3 PN码特性

3.3.1 自相关性和平衡性

1）通过本数据可以看出，初级系统的数据经过次级叠加使产生的数据量增加300倍.

3.3.2 信噪比对误码率的影响

当信噪比[5-8]在1～10 dB变化时，由图4可知截取序列的长度越长对系统误码率的影响越大，反之越短影响越小；从图5可知截取初级序列相同（2000点），若选取次级序列的变量不同，信噪比的影响不同，因而当选取相同序列时，变量输出的序列信噪比最小.

表1 0、1平衡性Tab.1 0、1 balance

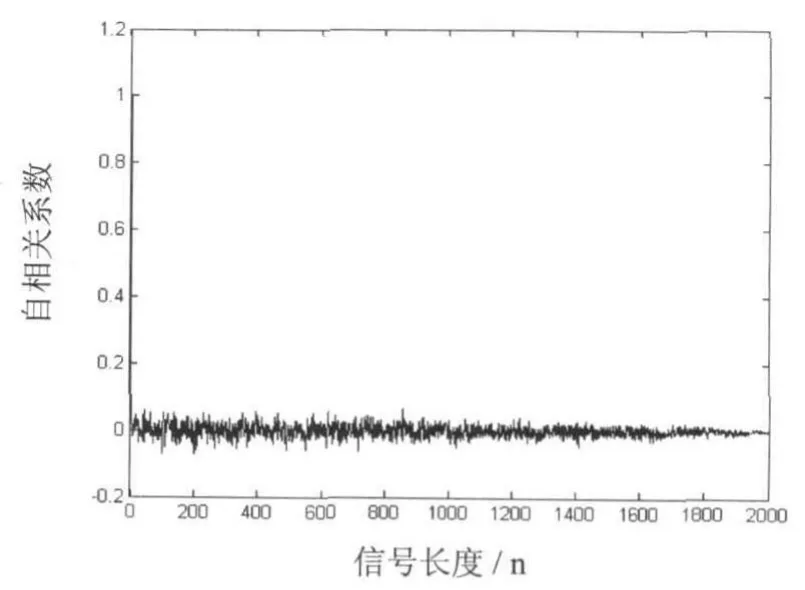
图3 自相关性Fig.3 autocorrelation coefficient

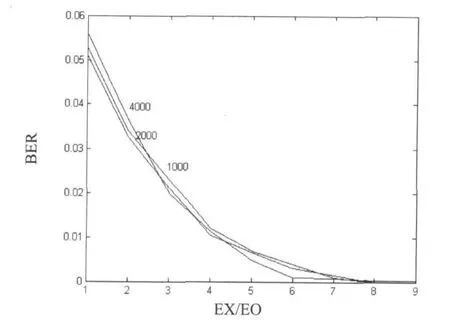
图4 信噪比和序列长度关系Fig.4 Relationship between SNR and the sequence length

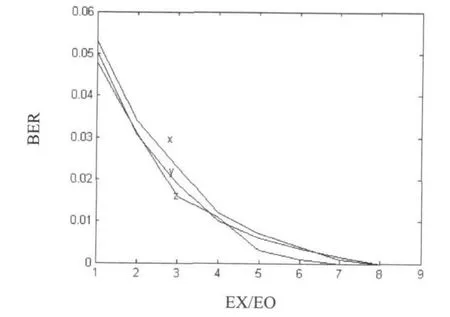
图5 信噪比和序列来源的关系Fig.5 Relationship between SNR and sequence sources

4 总结

1）随着初级混沌系统输出信号不断变化，次级混沌系统的分形参数在不断的变化，这样可使产生伪随机序列数目增多，可以有效的防止有用信息被破译，提高信息系统及有用信息保密性和抗攻击能力，也可增强序列的伪随机性能；

2）由于初始值、分形参数和迭代时间倍数可增加混沌序列的密钥空间，增强通信的安全性.

[1]Pecora LM，Carroll T L.Synchronized in chaotic systems[J].PhysRev Lett，1990，64：821.

[2]Carrol T L，Pecora LM.Synchronizing chaotic circuits[J].IEEETransCircuits Syst，1991，38（4）：453-456.

[3]Pang Jing，Ding Qun，Su Shuang chen，etal.Quickly determ ining themethod ofchaotic synchronizationsystem and itsapplication inspread spectru communication system[J].Communications in Computerand Information Science，2011，159（2）：242-246.

[4]丁群，杨自恒，庞晶，等.基于FPGA技术的离散混沌序列电路设计与实现 [C]//中国第19届电路与系统学术年会论文，合肥：2005.

[5]李长庚，周家令，孙克辉，等.基于M序列同步的混沌扩频通信系统研究与仿真 [J].系统仿真学报，2009，21（4）：1198-1201.

[6]黄乘顺，李星亮.基于混沌的扩频通信系统及性能分析 [J].通信技术，2008，41（12）：37-39.

[7]于娜，丁群，陈红.异结构系统混沌同步及其在保密通信中的应用 [J].通信学报，2007，28（10）：73-78.

[8]孙克辉，周家令，牟俊.多用户混沌序列扩频通信系统设计与性能分析 [J].电子与信息学报，2007，29（10）：2437-2440.

[9]庞晶，张国勇，苏双臣，等.基于genesio混沌同步和反同步系统的设计及其在扩频通信的应用 [J].河北工业大学学报：自然科学版，2011，40（2）：16-19.