一个习题的注记
王颖俐,王慧群,王 鑫
(1.长治学院 数学系,山西 长治 046011;2.长治县第一中学,山西 长治 047100)
秩为1的矩阵的结论看似很浅显,其实它的应用很广泛。
习题[1]设A是一个n×n矩阵,r(A)=1。

这个习题是选自王萼芳、石生明所编写的《高等代数》(第三版)中第四章补充题第1题。这个习题的结论形式很简单,但是由该习题所引发的思考是源源不断的。文章就从该习题出发,讨论了该习题的两个应用:一个是一致矩阵;一个是二维离散型随机变量独立性的矩阵刻划。
1 一致矩阵
定义1:正互反矩阵[2]
对任意两个因素Ci和Cj,用aij表示Ci和Cj对目标层的影响程度之比,按1~9的比例标度来度量aij.于是,可得到两两成对比较矩阵A=(aij)n×n,又称为判断矩阵,显然 aij>0,aij=,aij=1(i,j=1,2,…,n).
因此,又称判断矩阵为正互反矩阵.
定义 2:一致矩阵[2]
一般地,如果一个正互反矩阵A满足aijakj=aij(i,j,k=1,2,…,n),则称 A 为一致性矩阵,简称为一致阵.
一致矩阵具有以下性质:
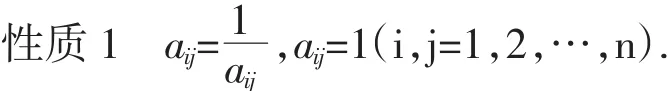
性质2矩阵A的各行成比例,且r(A)=1.

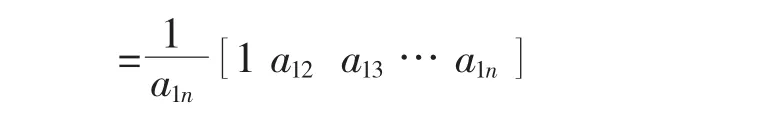
从而可得矩阵A的各行成比例,且r(A)=1
性质3 矩阵A的转置AT也是一致矩阵,且

性质4 若矩阵A为一致矩阵,则:

性质5 矩阵A的最大特征根为λ=n,其余n-1个特征根均等于0.
性质6 矩阵A的任一列(行)都是对应于特征根n的特征向量.
证明:(1)先证列成立
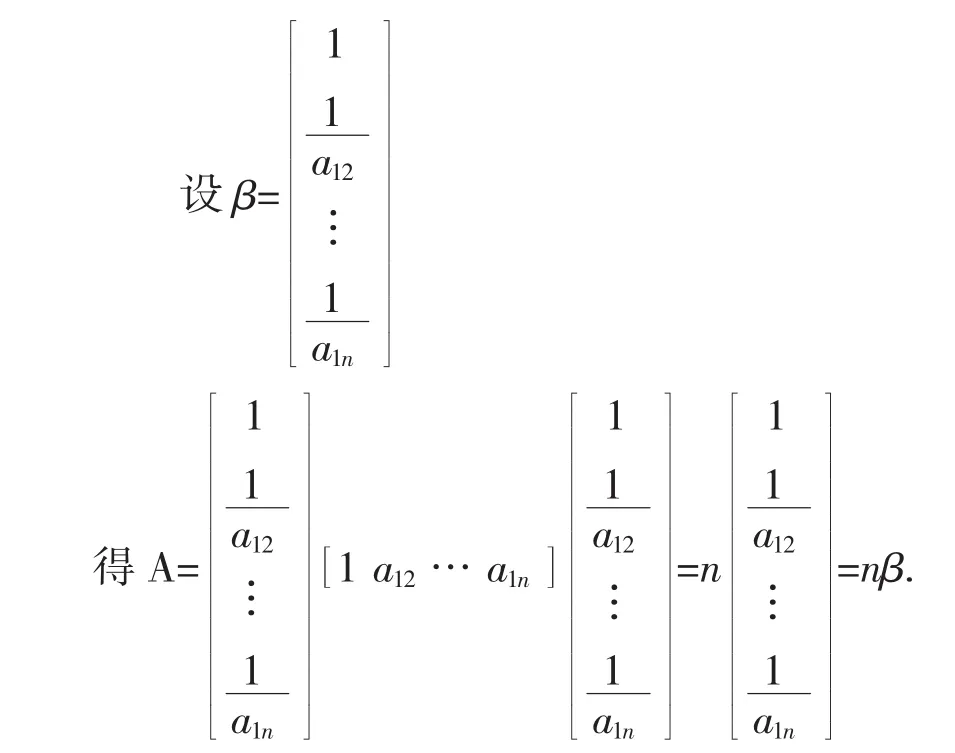
因此,矩阵A的任一行都是对应于特征根n的特征向量.
(2)再证行成立
由于一致矩阵A还可以表示为:


因此,矩阵A的任一列都是对应于特征根n的特征向量.
2 二维离散型随机变量独立性的矩阵刻划
设(X,Y)是二维离散型随机变量[4],X 与 Y 相互独立,(X,Y)的联合分布律为

设X、Y的边际分布律分别为:
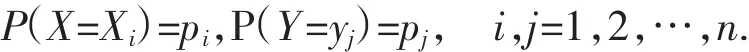
由X与Y相互独立,得

即:pij=pi.pji,j=1,2,…,n.
(X,Y)的联合分布律为:
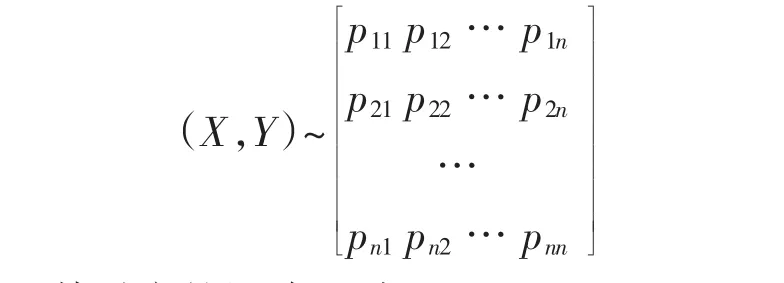
其对应的矩阵A为:
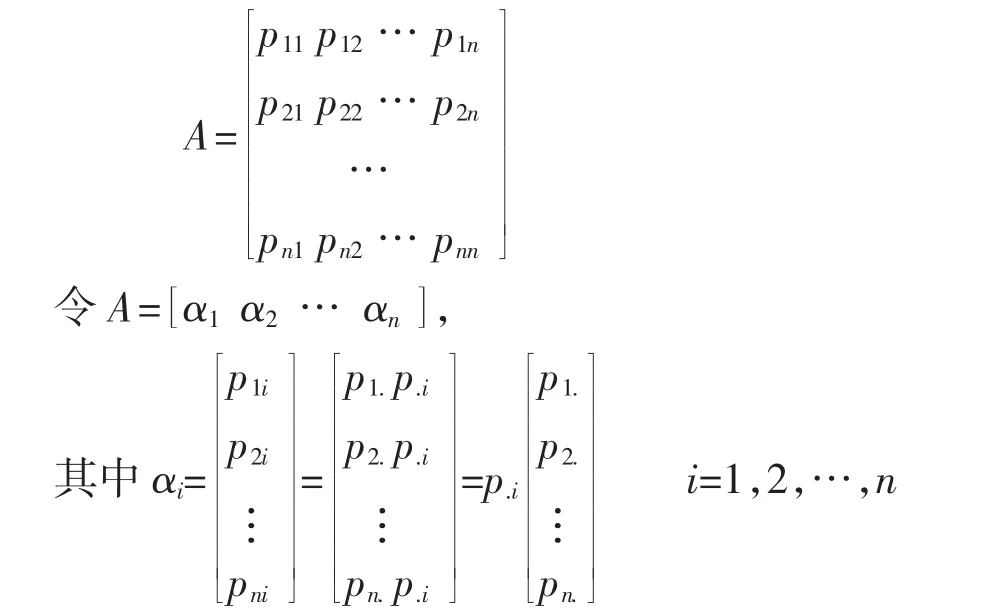
因此,A的各列成比例,从而r(A)=1,且
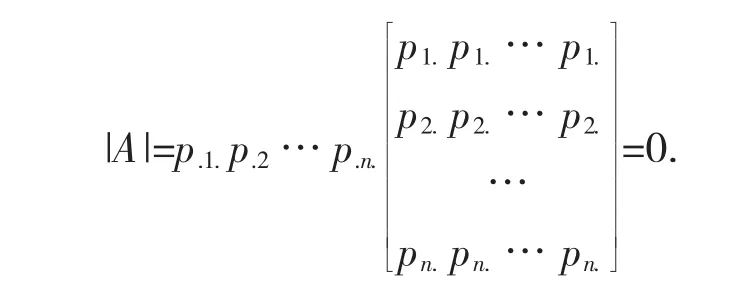
这说明若二维随机变量X与Y相互独立,则由(X,Y)的联合分布列所构成的矩阵A的秩为1,且其行列式为0.
反过来,若已知(X,Y)的联合分布列所构成的矩阵A的秩为1,则A的任意二阶以上的子式都为零,从而:

从而得X与Y相互独立.
因此我们可以得到二维离散型随机变量(X,Y)独立的充要条件是(X,Y)的联合分布列所构成的矩阵A的秩为1.
[1]王萼芳,石生明.高等代数(第三版)[M].北京:高等教育出版社,2003.
[2]韩中庚.数学建模方法及其应用(第二版)[M].北京:高等教育出版社,2004.
[3]吴文江.一致性正矩阵的一个性质的另一证法[J].山东建材学院学报,1995,9,10(3):65-66.
[4]韩旭里,谢永钦.概率论与数理统计(修订版)[M].上海:复旦大学出版社,2006.

