基于输出函数的滑模励磁控制器研究
张耀天,马 伟,艾吕泽,李 放
(1.成都电业局,四川 成都610001;2.邢台电业局,河北 邢台054001;3.东北电力大学电气工程学院,吉林 吉林132012)
0 引言
励磁控制系统对电力系统的小干扰稳定性和暂态稳定性起着至关重要的作用,所以,精确线性化、H∞鲁棒控制、变结构控制等非线性控制方法和智能控制方法在电力系统中的励磁控制中得到了充分应用[1-8]。文献[9]使用逆推的方法逐步构造李雅普诺夫函数来保证系统的正定性,最后使用反馈线性化得到控制规律,仿真结果证实了该方法的有效性。文献[10]使用Terminal滑模方法设计了励磁控制器,能够估计扰动的上下界,使设计的控制器具有一定的鲁棒性。文献[11]采用反推逐步求解的方法,逐步构造出滑模超平面,通过逐步构造Lyapunov函数,设计了一种鲁棒励磁控制器。但上述这些方法设计的控制器形式比较复杂,因此,本文提出选取输出函数的输出变量组成滑模面,通过对其求导得到滑模面为状态变量的状态方程,构造李雅普诺夫函数来保证整个系统的稳定性,对含有励磁电压的状态方程进行反馈线性化。使设计的控制器更加简单实用。
1 数学模型
本文采用的三阶发电机模型表达式为

机端电压Ut的状态方程为

式中:机端电压的d轴分量Ud=xqIq;机端电压的q轴分量 Uq=E′q- x′dId。
式(1)可写成如下的形式:

考虑系统的输出变量,系统可扩展为

2 滑模控制
滑模控制主要目的是通过选取适当的状态变量的线性组合组成切换面,然后通过引入李雅普诺夫函数来保证系统的正定性。
设状态变量的跟踪值为xref,则跟踪误差表达式为

即系统的跟踪误差与系统的输出相同。
定义滑模面为

式中:c=[c1,c2,c3]。滑模控制器的设计的主要任务之一就是行向量c的确定。
定义对应的李雅普诺夫函数为

针对三阶系统,有 s=c1ΔPe+c2Δω +c3ΔUt,则



将式(7)代入式(6),得

本文采用准滑动模态控制原理,即用饱和函数sat(s)代替滑动模态中的符号函数sign(s),sat(s)的表达式为

式中:Δ为边界层。
经过替换之后的式(9)变为


依然能够保证导数的负定性,即由式(8)和式(9),可以得出

由(15)可以得出

由于a(s)和b(s)的表达式比较复杂,含有较多的系统状态变量和参数,所以通过ESO来观测该部分,将其作为未知扰动部分处理。
3 扩张状态观测器(ESO)
因为系统的非线性变量包含在含有滑模面的一阶方程中,所以只需构建二阶的ESO即可,其表达形式为

式中:z1为s的估计值;z2为扩张变量;
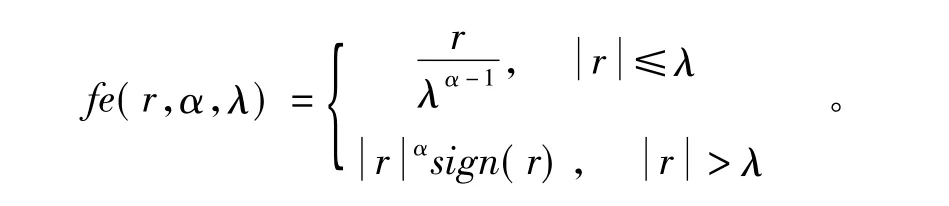
对于经过ESO反馈之后的式(8)所表示的系统控制输入表达式为

4 设计步骤和仿真分析
励磁控制器的设计步骤如下:
1)选取新的坐标系和状态变量e=Y=[Pe-Pe0,ω - ω0,Ut- Ut0]T。
2)构造李雅普诺夫函数,并选取滑模面s=cY=c1ΔPe+c2Δω +c3ΔUt,并从其对应的导数式中得到滑模控制输入的表达式为,其中R= -ks-εsat(s)。
3)构造二阶的扩张状态观测器,得到对应的滑模控制器对应的控制变量
本文算例中单机无穷大系统的主要参数如下:
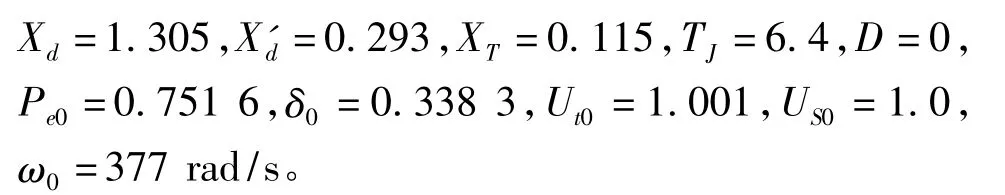
分别采用以下两种励磁控制器:
1)AVR+PSS,励磁系统AVR采用机端电压的偏差值作为输入信号,PSS采用转速的偏差作为输入信号。
2)本文设计的励磁控制器,其中ESO的参数

α1、α2、λ1的取法参见文献[12],β01、β02的确定可以根据z1-s目标函数,调用Simulink中的优化函数可得到。
滑模切换面的参数为

式中:c1=20;c2=-1 000;k1=22.22;c3=28;b0=0.28;ε1=0.2;Δ =0.1。参数 c1、c2、c3的选定可以使用极点配置法得到。
4.1 原动机输入扰动
在0.1 s时,原动机的输出功率Pm发生10%的阶跃扰动,动态响应曲线分别如图1、图2所示,其中实线代表励磁控制器,虚线则对应AVR+PSS控制器。
从图1、图2可以看出,在两种不同励磁控制器用下,图中所示的励磁控制器曲线均小于AVR+PSS。从仿真曲线上看,本文提出的励磁控制器使功率振荡受到一定的抑制。因此,该励磁控制器能够改善系统的小干扰稳定性。

图1 机械功率扰动时1号发电机电磁功率响应曲线
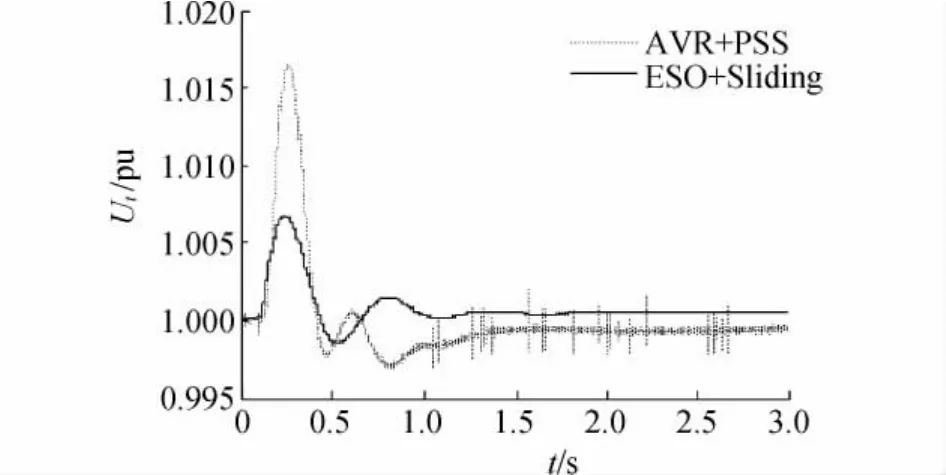
图2 机械功率扰动时1号发电机机端电压响应曲线
4.2 三相短路扰动
故障2为低压侧母线处0.1 s时发生瞬时三相短路,持续时间为0.1 s。有功功率Pe和机端电压Ut的动态响应曲线分别如图3、图4所示。

图3 三相短路扰动时1号发电机电磁功率响应曲线

图4 三相短路扰动时1号发电机机端电压响应曲线
从图3、图4可以看出,在两种不同励磁控制器用下,功率振荡时间分别为2.0 s、0.5 s。从仿真曲线上看,本文提出的励磁控制器使状态变量有效地抑制了振荡幅值,减少了调节时间。因此,该励磁控制器也可以改善系统的暂态稳定性。
5 结论
1)通过选取输出函数中的跟踪误差可以得到对应的滑模切换面,使系统的状态变量收敛于设定值。
2)李雅普诺夫函数的引入确保系统的整体稳定性,为控制器的设计提供了有利的依据。
3)扩张状态观测器的设计能够抵消系统的扰动,不依赖与系统的运行状态和参数,从而保证了控制器具有一定的鲁棒性。
[1]周双喜,汪兴盛.基于直接反馈线性化的非线性励磁控制器[J].中国电机工程学报,1995,15(4):281 -288.
[2]蔡超豪.非线性H∞励磁控制器的设计[J].电网技术,2003,27(3):50-52.
[3]姚舜才,潘宏侠.粒子群优化同步电机分数阶鲁棒励磁控制器[J].中国电机工程学报,2010,30(21):91-97.
[4]张风营,朱守真.基于强跟踪滤波器的自适应励磁控制器[J].中国电机工程学报,2005,25(23):31-35.
[5]万黎,邓长虹,陈允平.考虑机端电压限制的多重非线性变结构励磁控制[J].中国电机工程学报,2008,28(19):86-92.
[6]张凯锋,戴先中.多机电力系统励磁控制的人工神经网络逆系统方法[J].中国电机工程学报,2003,27(21):24 -30.
[7]徐庆宏,戴先中.多机电力系统附加NNPSS的在线学习神经网络逆励磁控制器[J].电力自动化设备,2010,30(1):25-31.
[8]兰海,李殿璞,杨丽华.多机系统励磁的非线性L2增益干扰抑制控制[J].电机与控制学报,2005,9(2):151-155.
[9]王宝华.逆推自适应滑模励磁控制器设计[J].电力自动化设备,2009,29(6):54-57.
[10]邹德虎,王宝华.发电机自适应Terminal滑模励磁控制[J].现代电力,2010 ,27(2):62-65.
[11]鲁升敏.基于反推方法的滑模自适应励磁控制[J].电网与清洁能源,2010,26(1):77-79.
[12]韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008.

