风机电力系统小干扰稳定域的研究

刘书成

(东北电力大学电气工程学院，吉林吉林132012)

0 引言

随着能源危机的不断加深，新能源的利用和开发也越来越受到人们的重视和青睐，风能作为一种清洁能源被纳入中国的能源长期规划范围之内［1］。由于风能具有一定的随机性，并入电力系统之后会给系统带来一定的冲击。因此，研究合理的风机接入容量的问题成为一个亟待解决的现实问题。而其中的重要一方面就是需分析风机接入后系统的稳定性的问题。对此，许多学者曾做出一些深入的研究［2－4］。如文献［5］分析了在不同运行状态下，风电并网前后互联系统的小干扰稳定性变化，对实际的稳定性分析提供了理论依据;文献［6］推导了双馈机组小干扰稳定的数学模型的基础上，以通辽外送型电网接入大规模风电为例，系统研究大规模风电外送对电力系统小干扰稳定的影响;文献［7］利用DIgSILENT/PowerFactory进行频域分析和时域仿真，分析异步风电机组对电力系统小干扰稳定性及阻尼特性的影响;文献［8］考虑同步发电机励磁调节系统动态行为的全系统状态矩阵公式;利用特征值分析法，分析了系统的小干扰稳定性。基于此，本文先介绍小干扰稳定分析的线性化理论，给出小干扰稳定域的条件，然后推导风机与同步机并联的系统的小干扰分析的雅克比矩阵，通过改变风机的输入功率和原动机的机械功率，得到对应的小干扰稳定域。

1 小扰动稳定域的边界

对同时含有微分方程和代数方程的非线性系统，数学表达式为

式中:x为系统状态变量;y为代数变量;p为控制变量。对系统式(1)在平衡点处线性化，可得:

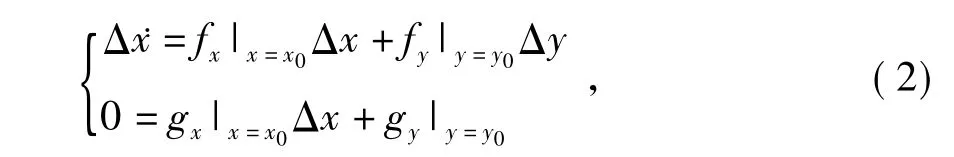
式中:fx、fy、gx、gy分别为函数对状态变量和代数变量的偏导数。

若矩阵gy非奇异，则式(2)可写为

式中:A(p)=fx－fygy－1gx。

当gy非奇异且A(p)的特征根具有负实部时，得出的小扰动稳定域是稳定的。

根据式(3)的方程，选择适当的算法得到稳定域的步骤如下:

1)选定需要变化的参数值，将其它参数设定为常数。

2)确定参数的初始点，一般选择系统稳态的参数值作为初始值。

3)在对应的参数空间中，从初始点沿某个特定的方向，并以适当的步长改变系统的参数值，得到给1个点对应的雅可比矩阵特征值。

4)当参数出现1对共轭纯虚特征值且其余特征值均有负实部时，系统发生HB，记录此时的参数，并停止该方向的搜索。

5)改变3)步骤中搜索边方向，重复3)和4)步骤，得到新的边界点。该方法在参数空间(p1，p2)中占用较多的计算时间，但具有较好的准确性，可根据上个步骤的特征值自适应地调整步长，进而增加该方法的灵活性。

在具有多个发电机的电力系统中，若考虑发电机注入功率为分岔参数时，对应的小干扰稳定域比发电机台数少一维的超平面;当SSSR的维数大于三维时，已经失去了直观形象的优点。常见的方法是将其投影到低维平面中，使其具有一定的实用价值，但也丧失很大一部分的有用信息。1个有价值的方案是按照二机等值的方法，将n－1维的曲面投影到n－1个2维空间上，节省了计算量，具有直观的物理意义［9］。

2 含有异步风机的电力系统

2.1 异步风力发电机组数学模型

2.1.1 风力机数学模型

风力机机械功率为

风力机机械转矩方程为

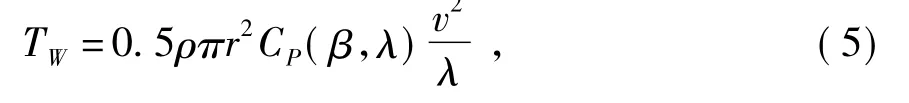
式中:PW为风力机机械功率;TW为风力机机械转矩;r为风力机叶轮半径;ρ为空气密度;β为桨距角;λ=rω/v为叶尖速比;ω为风力机转速;Cp为风能转换效率系数;v为风速。

连接叶片和齿轮箱的轮毂，有较大惯性，其两边的转矩可用一阶惯性环节模拟，其表达式为

式中:Tt为输入齿轮箱的机械转矩;τh为轮毂的惯性时间常数。

齿轮箱和联轴器传递风力机和异步发电机间的转矩，其方程表达式为

式中:Tm为齿轮箱输出转矩;Tt为异步发电机输入转矩;ττ为齿轮箱惯性时间常数。通常认为风力机转速基本保持不变，有 Tm≈Tt。

传动部分模型方程表达式为

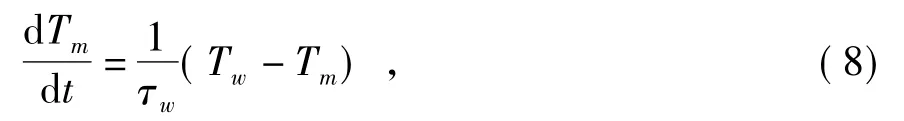
式中:τw为风力机惯性时间常数。

2.1.2 桨距角控制系统数学模型

通过调节叶片桨距角，使风力机跟踪 Cp达到最大值，提高风能利用效率。桨距角控制系统通常表示为

式中:β0为桨距角初始值;τβ为桨距角控制系统的惯性时间常数。

2.1.3 异步发电机组数学模型

简单的风机系统的方程主要包括定子电压方程、机电暂态方程以及转子电压方程等。

定子电压方程形式为

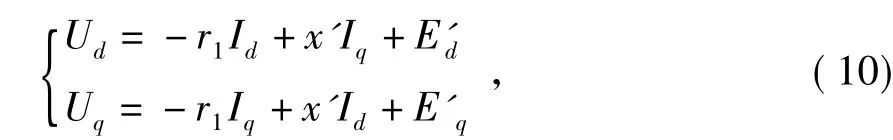
机电暂态方程形式为

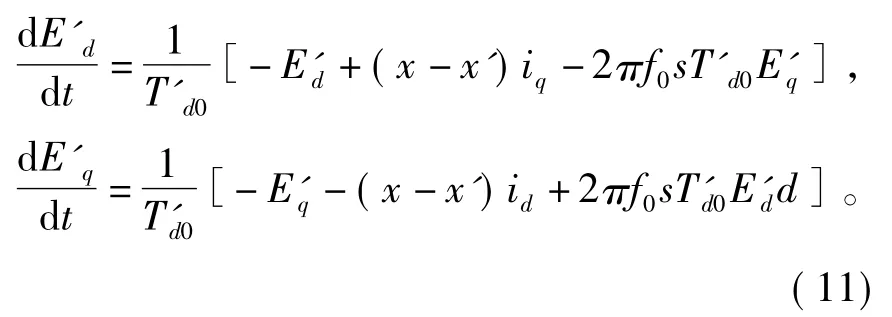
而发电机的暂态电抗为

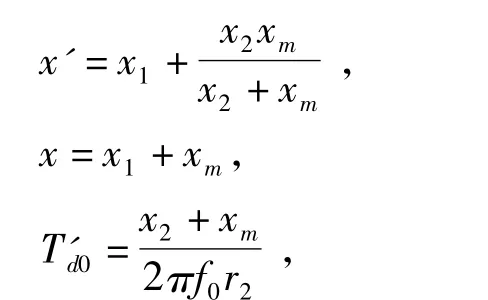
式中:Ud、Uq分别为发电机定子电压 d、q轴分量;Id、Iq分别为定子电流 d、q 轴分量;E′d、E′q分别为暂态电势 d、q轴分量;T′d0为定子开路时间常数;r1、r2、xl、x2、xm分别为异步发电机定子电阻、转子电阻、定子电抗、转子电抗和激磁电抗标么值。

转子运动方程为

式中:τj为异步发电机的惯性时间常数;s为转率差;Te为电磁转矩。

将式(13)线性化方程为

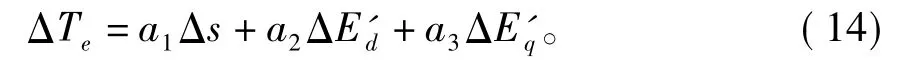
整理上述微分方程，并对其进行在平衡点处进行线性化分析，得到以 Δβ、ΔTt、Δs、ΔE′d、ΔE′q为状态变量的异步风电机组状态方程为

式中:ids0、iqs0为定子电流的 d、q 轴分量;E′d0、E′q0为暂态电势的d、q轴分量。

将式(15)简写为

2.2 同步发电机组数学模型

同步发电机的三阶模型为

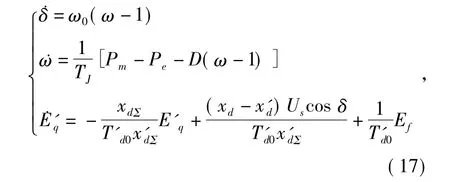
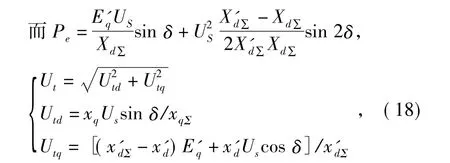
式中:δ为发电机功角;ω为发电机转速;ω0为发电机的稳态转速;TJ为机械转动惯量;D为机械阻尼系数;Pm为原动机机械功率;Pe为发电机电磁功率;Eq为q轴暂态电势;Ef为励磁的控制输入;Td0′为发电机定子开路时励磁绕组的时间常数;Ut为发电机机端电压;Us为无穷大母线电压;xd为发电机的d轴同步电抗;xd∑为计入了输电系统总电抗后的d轴总同步电抗;xd′为发电机d轴暂态电抗;xd∑′为计入了输电系统总电抗后的d轴暂态总电抗。

对其在平衡点处进行线性化，可得到类似于式(15)的矩阵，将其写为

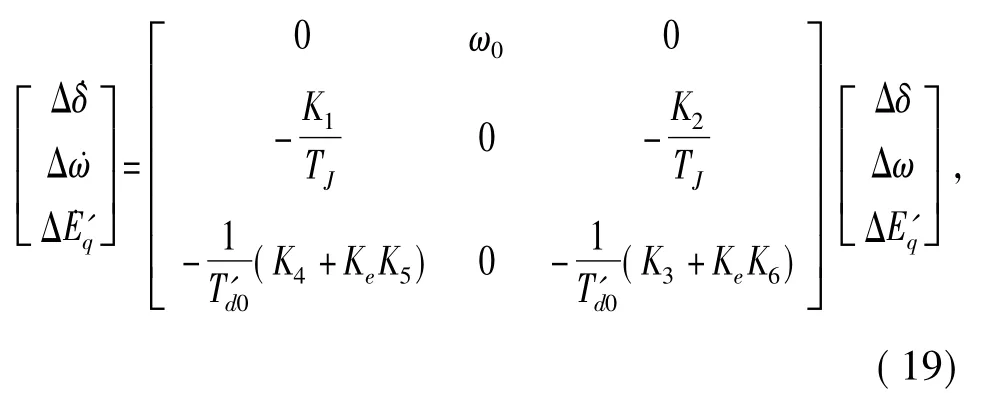
式中:(19)式的参数的形式和含义见文献［11］。

式(19)同样可以简写为

ΔY˙=A2ΔY。

将式(15)和式(19)联立，可得

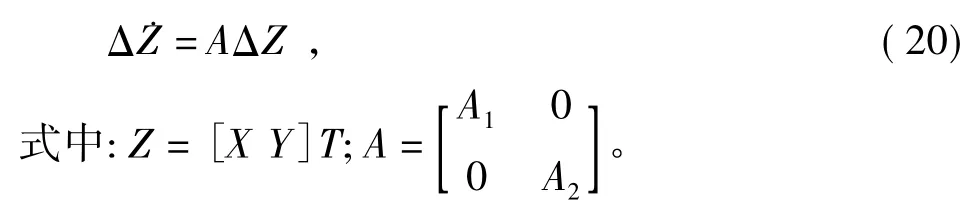
3 算例分析

3.1 系统的主要参数

为了验证本文算法的有效性，特引入1组风机与单台同步机并联的系统，然后与输电线路域无穷大系统相连。算例系统如图1所示。其中，1组风机可以简化为单台的异步发电机，具体的等值方法见文献［10］。同步机的主要参数如下:

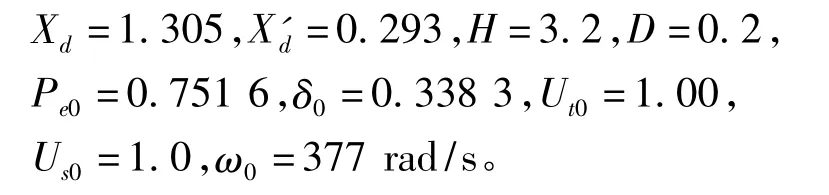
线路及变压器的参数为

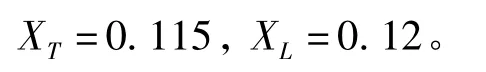
单台异步风力发电机的主要参数如下:

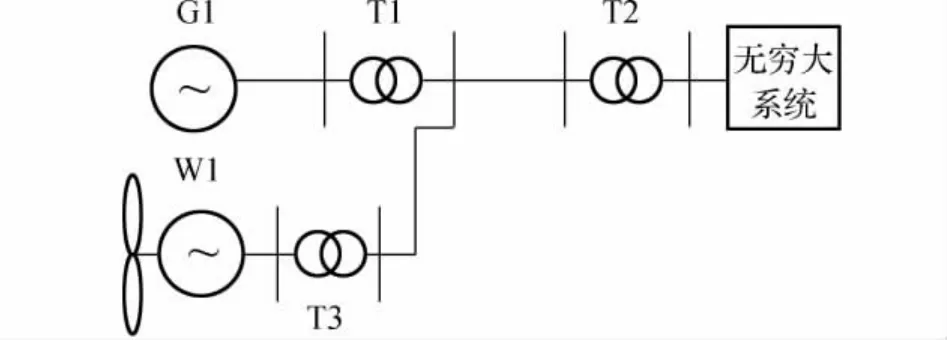
图1 算例系统

分别令风机的输入机械功率PW和发电机的输入机械功率Pm为自变量，根据式(3)可得到对应的小干扰稳定域，如图2所示。

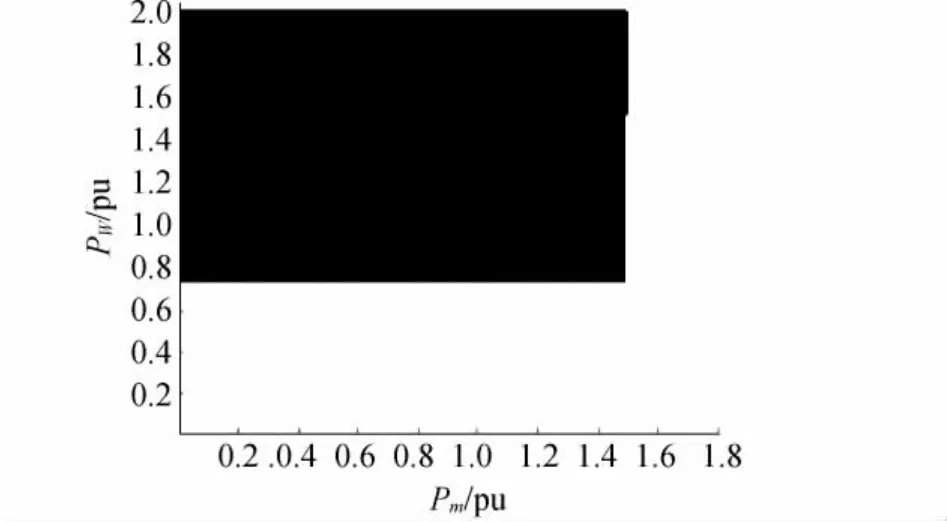
图2 本文所示系统的小干扰稳定域

从图2可以看出，阴影部分对应的为系统的小干扰稳定域，异步风力发电机维持在较高出力水平，同步发电机维持在正常出力水平下就可维持系统的小干扰稳定。若不满足上述条件，则有可能出现系统的振荡，需要其它辅助措施才能维持系统的小干扰稳定性。

3.2 励磁放大倍数对小干扰稳定域的影响

励磁放大倍数作为电力系统的重要参数，对电力系统的稳定性具有一定的影响。因此，在这里通过改变励磁放大倍数，可以得出对应的小干扰稳定域。通过对比可知放大倍数对小干扰稳定域的影响。Kv=5时的小干扰稳定域如图3所示，Kv=20时的小干扰稳定域如图4所示。

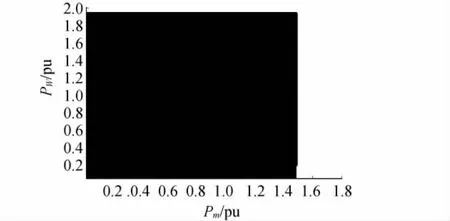
图3 Kv=5时的小干扰稳定域

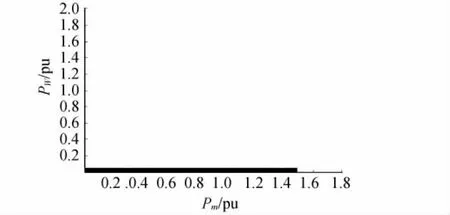
图4 Kv=20时的小干扰稳定域

通过对比图2、图3、图4(其中图2为励磁放大倍数为10的稳定域)阴影部分，可以看出励磁放大倍数对系统的小干扰稳定域有相当大的影响，主要是对异步风力发电机出力影响较大，对同步机出力基本上没有影响，说明实际系统中合理配置系统的励磁放大倍数，对系统的稳定性具有至关重要的作用。

4 结论

通过线性稳定性理论研究了含有风机系统的小干扰稳定域问题，得到如下结论:

1)系统的稳定性是由异步风机和同步发电机相互协调决定的，两者的出力水平需要保持在适当水平才能保证系统的稳定性。

2)励磁放大倍数对系统的稳定性具有重要的影响。但相对而言，对异步风力发电机的出力影响很大，对同步发电机没有很大变化。

［1］雷亚洲．与风电并网相关的研究课题［J］．电力系统自动化，2003，27(8):84 －89．

［2］张卫红，于吉庆，王坤．新能源发电并网标准比较［J］．黑龙江电力，2011，33(6):403－408．

［3］申洪．变速恒频风电机组并网运行模型及其应用［D］．北京:中国电力科学研究院，2003．

［4］吴义纯，丁明，张辉．含风电场的电力系统潮流计算［J］．中国电机工程学报，2005，25(4):36－39．

［5］符杨，霍淑珍，边晓燕，等．基于NEVA的风电并网小干扰稳定研究［J］．华东电力，2011，39(3):443－445．

［6］杨涛，郑涛，迟永宁，等．大规模风电外送对电力系统小干扰稳定性影响［J］．中国电力 ．2010，43(6):20－25．

［7］关宏亮，迟永宁，戴慧珠，等．异步风电机组接入系统的小干扰稳定及控制［J］．电力系统自动化，2008，32(4):54 －58．

［8］范伟，赵书强．考虑风力发电的电力系统小干扰稳定性分析［J］．华北电力大学学报，2009，36(2):23 －27，32．

［9］郝正航，陈卓．注入功率空间上电力系统小扰动稳定域的实用边界［J］．电工电能新技术，2011，30(3):38－42．

［10］李桂红．含风电场电力系统小干扰稳定分析［D］．太原:太原理工大学，2010:34－37．

［11］李光琦．电力系统暂态分析［M］．北京:中国电力出版社，2007:184－187．