空间网架结构随机地震动激励下的响应分析
张青雷, 张小兵, 郭井宽
(1.上海理工大学 机械工程学院,上海200093;2.上海电气集团股份有限公司 中央研究院,上海200070)
空间网架结构是由杆件按照一定的网格形式通过节点连接而成的空间杆系结构.具有空间受力、重量轻、刚度大、抗震性能好等优点.现在被广泛地应用于大跨度车间、体育场馆、车站、机场等场所,作为重要的公共设施,其地震安全性对于设施的正常运转和公众的财产安全至关重要[1].地震发生时,从震源释放出来的能量以地震波的形式传至地面,而在地震波传输的过程中经由不同的路径、不同的地形地质条件,所以反映到地表的震动必然存在差异.这种差异主要是由于地震波以有限波速传播引起的行波效应;地震波在介质中传播时发生反射和散射,同时由于从震源不同位置传到地表不同点处地震波叠加方式的不同,导致相干性部分损失;各支承点所在场地土层性质可能存在差异,导致地震动通过不同地基土到达各支承点处输入地震动不同[2-3].因此,研究大跨度空间网架结构在多点输入下结构的地震反应很有必要[2,4].
目前计算结构对多点输入的反应时,主要的研究方法有:确定性动力分析法、随机振动分析法和工程实用反应谱法[2,5].对于确定性动力分析法来讲,如果选择的地震波与场地的实际情况不同,则无法得出正确的结论[2,5-6];对于反应谱法而言,反应谱的组合方式是基于平稳随机过程理论而得到的分析方法.事实上,地震动是强烈的非平稳随机过程[2,5].随机振动分析方法建立在各点地面运动的统计特征基础上,在确定了地震动场的自功率和互功率谱后,可以计算出各反应量的统计规律[2,5].而地震地面运动本身就是一个随机场,采用随机振动分析方法日益受到重视[2].通过以上的对比,本文采用随机振动分析法,对大跨度空间网架结构进行地震响应分析.
1 运动方程
地震动多点激励下的结构运动方程
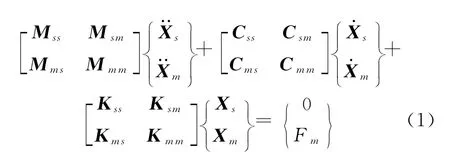
式中,M为结构的质量矩阵;C为结构的阻尼矩阵;K为结构的刚度矩阵;X为结构的位移矩阵;Fm为随时间变化的载荷矩阵.其中,下标m为地面强迫位移相应的自由度;s为结构的其它可动自由度.
由式(1)可得,网架结构的平衡方程按在支撑处指定的绝对位移为

当忽略阻尼力的影响同时考虑质量矩阵为对角矩阵时,式(2)可以进行进一步简化为
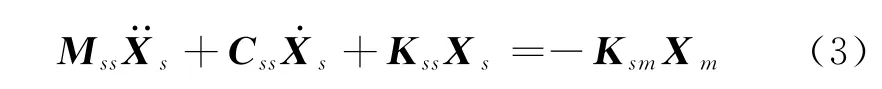
绝对位移可以分解为两部分[7],即拟静位移和动态位移
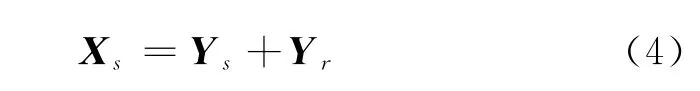
其中拟静位移向量Ys,应满足
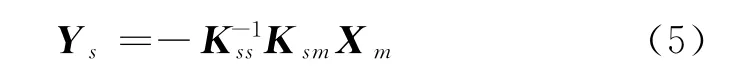
动态位移Yr在用于均匀地面运动加速度激励时,为了求解式(4)能够与常规计算结果一致,假定阻尼力与相对速度成正比[8],则动态位移应该满足

其中

2 随机地震动模型及其参数确定
采用修 正 Clough-Penzien 谱[5,9],计 算 得 出 加速度功率谱密度函数
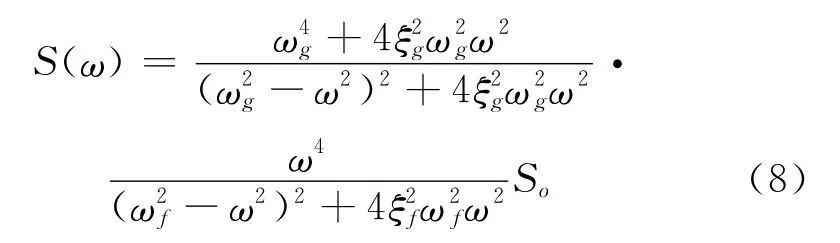
式中,So为谱强度因子;ξg和ωg分别为地基土的阻尼比和卓越频率;ξf和ωf为模拟地震动低频分量能量变化的参数.结构所在的场地抗震设防烈度定为8度,Ⅱ类场地土,罕遇地震作用[10].各参数根据文献[3]进行取值

由计算机拟合出该功率谱密度函数的曲线,如图1所示(见下页).
3 结构模型
选取上海大众仪征五厂的车身车间的网架结构作为研究对象,建立有限元模型.该网架为正放四角锥网架,共有3 501个节点,14 072根杆件,其中杆件的截面尺寸有17种,支撑柱有4种截面尺寸;网架的平面尺寸为216m×120m;下部采用60柱支承,柱高10.3m,间距24m.该结构的有限元模型如图2所示.

图1 地震动加速度自功率谱密度函数曲线Fig.1 Power spectral density function curve of earthquake acceleration
在结构的计算分析中,钢材的弹性模量取为210MPa,采用Rayleigh阻尼,振型阻尼比取为0.02.杆件与杆件之间和杆件与支撑柱之间的连接假定为铰接,支承柱与基础的连接方式假定为钢接.

图2 网架结构分析模型Fig.2 Analytical model of spatial grid structure
4 模态分析
模态分析是结构的动力学分析的基础.模态分析的主要任务是计算结构的固有频率f和模态振型.采用Block Lanczos法对该模型进行模态计算,取阶数n为10阶进行分析.结果如表1所示.
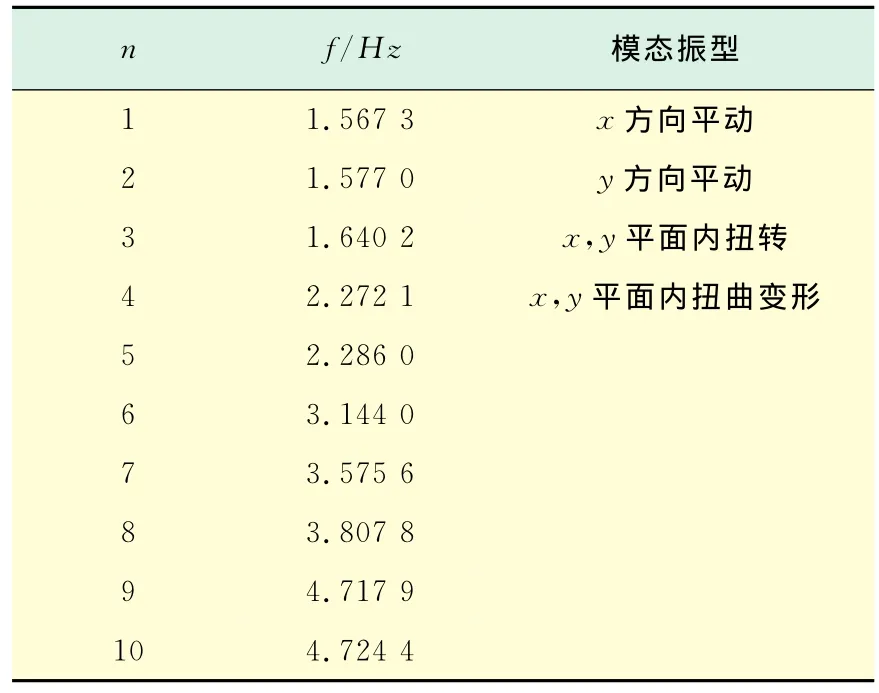
表1 结构振动特性Tab.1 Structure vibration characteristics
从模态分析的计算结果可知,该结构自振特性具有振型密集,频率变化均匀的特点,体现了该结构动力特性的复杂性.第一阶振型为x方向平动,第二阶振型为y方向平动,而且两者的周期比较接近;第三阶振型为绕z轴的扭转振型,以转动为主的第一自振周期T3与以平动为主的第一自振周期T1的比值T3/T1=1.567 3/1.640 2=0.96>0.9,由文献[11]可知该结构的扭转刚度小于其平动刚度,地震中容易发生扭曲破坏.
5 杆件的受力分析
随机振动分析采用功率谱密度作为输入,是一种确定响应出现特征值的概率大小的分析方法.随机振动分析时,需要设定结构的阻尼系数,对试验测得的0~100Hz频段的模态分析均按照阻尼系数为0.02计算.根据随机振动分析理论,得到的分析结果具有统计特性,显示的结构变形为均方根变形.图3为该网架结构在x,y,z方向的随机地震动激励作用下杆件的应力值.
由图3(a)可知,在水平方向的随机地震动激励作用下,该空间网架结构下弦中有几根杆的应力值σ超出其许用应力值210MPa(见表2),这些杆件发生破坏,其中最大应力值出现在1号杆为713MPa.图3(b)和(c)上弦和腹杆的杆件应力值均在安全范围内.由文献[11-13]可知,由于该结构是正放四棱锥形式,超静定次数高,当有几根杆件破坏时,结构内部会发生内力重分布现象,使结构继续有能力承载.将发生破坏的杆件去除,然后进行地震动激励,其余杆件的应力值均小于其许用应力.因此,该结构在地震动激励下并未发生破坏.

图3 x,y和z方向地震动激励作用下的杆件拉压应力值Fig.3 Draw-press stresses in bars of spatial grid structure under x,y,z directional earthquake excitation

表2 失效杆件表Tab.2 Failure rods
由图3可知,在x、y和z3个方向的随机地震动激励作用下,杆件的应力分布比较均匀,但是由图3(c),在x和y方向的地震动激励作用下,上弦中采用1号截面尺寸的杆件的应力值明显大于其它杆件.由图4(a)可知,在x和y方向的地震动激励下,腹杆杆件的拉压应力值变化较大.又由图4(b)和图4(c)可知,对于x和y方向的地震动激励作用,下弦的杆件和上弦中除1号截面杆件以外的其它杆件的拉压应力值变化幅度较小.总之,该结构在随机地震动激励作用下,杆件应力的整体分布表现出了良好的均匀性[14].
6 结 论
以上海大众仪征五厂车身车间的网架为例,基于随机振动理论对该结构进行3个方向的地震动激励作用下的结构随机响应分析.通过以上计算研究得出以下结论:
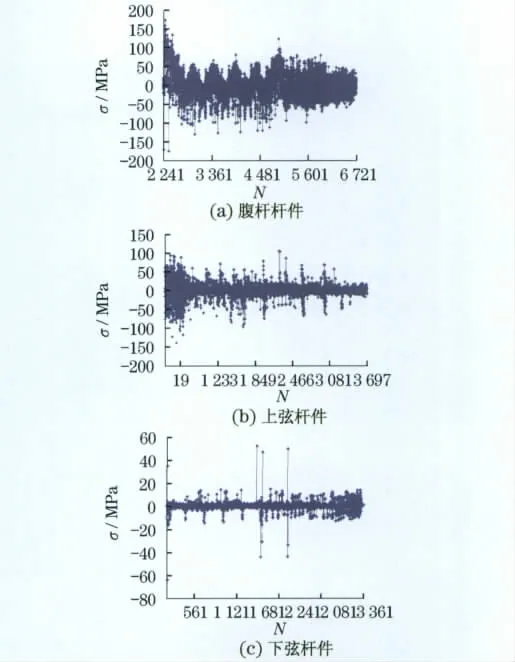
图4 水平x和y方向地震激励下杆件产生的拉压应力的差值Fig.4 Stress diversity generated by bars under the earthquake excitation in horizontal x and y directions
a.由模态分析的结果可知,该结构具有振型密集,频率变化均匀的特点,体现了该结构动力特性的复杂性;在地震动激励作用下该结构可能首先发生扭曲破坏.
b.该结构属于超次静定结构,在水平x和y方向的随机地震动激励作用下,虽然该结构下弦中的几根杆件发生破坏,但是结构内部发生内力重分布现象,使结构继续有能力承载.因此该结构整体安全.
c.在水平x和y方向的随机地震动激励作用下,上弦中采用1号截面尺寸的杆件应力值较大,不同激励方向对下弦的杆件和上弦中除1号截面杆件以外的其它杆件的应力值变化影响较小.
[1]董石麟.中国空间结构的发展与展望[J].建筑结构学报,2010,31(6):39-50.[2]潘旦光,楼梦麟,范立础.多点输入下大跨度结构地震反应分析研究现状[J].同济大学学报,2001,29(10):1213-1219.
[3]白凤龙,李宏男.地震动多点激励下大跨度空间网架结构的反应分析[J].工程力学,2010,27(7):67-73.
[4]甘明,张胜.空间结构抗震、抗风设计审查要点介[J].建筑结构,2009,39(12):106-110.
[5]林家浩,张亚辉,赵岩.大跨度结构抗震分析方法及近期进展[J].力学进展,2001,31(3):350-358.
[6]李忠献,林伟,丁阳.大跨度空间网格结构多维多点随机地震反应分析[J].地震工程与工程振动,2006,26(1):57-62.
[7]林家浩,张亚辉.随机振动的虚拟激励法 [M].北京:科学出版社,2004.140-141.
[8]Zhang Y H,Li Q S,Lin J H,et al.Random vibration analysis of long-span structures subjected to spatially varying ground motions[J].Soi Dynamics and Earthquake Engineering,2009,29(4):620-629.
[9]Wei Gao.Random seismic response analysis of truss structures with uncertain parameters[J].Engineering Structures,2007,29:1487-1498.
[10]薛素铎,王雪生,曹资.基于新抗震规范的地震动随机模型参数研究[J].土木工程学 报,2003,36(5):5-10.
[11]中华人民共和国建设部,中华人民共和国国家质量监督检验检疫总局.GB50009-2001建筑结构载荷规范[S].北京:中国建筑工业出版社,2006.
[12]约翰·-奇尔顿.空间网格结构[M].高立人,译.北京:中国建筑工业出版社,2004.
[13]Nafday A M.System safety performance metrics for skeletal structures [J].Journal of Structural Engineering,2008,134(3):499-504.
[14]沈顺高,张微敬,朱丹,等.大跨度机库结构多点输入地震反应分析[J].土木工程学报,2008,41(2):17-21.

