基于改进免疫遗传算法的骨折创伤断面生理刺激应力寻优方法

朱坚民， 周冬儿， 翟东婷

（上海理工大学 机械工程学院，上海 200093）

应力环境是影响骨折修复的重要因素，应力调整骨的生长和吸收，适宜的应力环境可以促进骨折愈合朝着最佳水平发展，相反则可导致不良后果.因此，对于骨折创伤断面的刺激应力，存在着一个最佳的应力范围，控制骨折愈合过程中创伤断面上的生理刺激应力按最佳应力发展，可以有效地保证骨折愈合的速度和质量.

Jorgensen于1979年通过应变片技术对固定器固定后骨折区进行生物力学测定，提出外固定器固定后理想的骨折愈合曲线应呈双曲线变化［1－5］.文献［1－2］研制了一种带微型力传感器和自动施力机构的骨外固定器，并对活体山羊骨折愈合中创伤断面的应力进行了实时测量，获得了山羊骨折创伤断面的应力变化曲线.这些应力变化曲线间接反映了骨折创伤断面的应力响应特性，但如何根据实测应力曲线通过相应的寻优算法探索骨折愈合各阶段的最佳生理刺激应力一直是难以解决的问题［3－5］.

遗传算法是目前发展最快的优化算法之一，它对优化问题的数学要求低，可以是线性或非线性、离散或连续优化问题，能进行概率意义上的全局搜索，已被广泛应用于各种优化问题.标准遗传算法是由密歇根大学Holland教授1975年首先提出，是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，并通过模拟自然进化过程搜索最优解.近年来，遗传算法被广泛用来解决许多复杂的搜索及优化问题.标准遗传算法过于注重对搜索空间中新区域的探索，忽略对现有解空间开发，存在局部搜索能力差、易“早熟”及后期进化效率低等问题［6－11］.针对标准遗传算法存在的问题，有学者借鉴免疫系统中抗体多样性、抗体浓度调节及免疫记忆的特征提出了免疫遗传算法.与标准遗传算法相比，免疫遗传算法重视对解空间的开发，能够保证解空间搜索区域的宽度，已在生产调度、自动控制、函数优化等领域得到了成功的应用［12－19］.但普通免疫遗传算法依然存在以下问题：a.算法中的抗体更新方法影响了抗体种群基因模式的多样性，限制了算法优化性能的进一步提高；b.算法的变异概率不能随着种群模式的动态变化而进行相应调整，使算法的收敛速度有待进一步提高.

针对以上问题，本文建立了骨折愈合中创伤断面生理刺激应力的寻优模型，对普通免疫遗传算法的抗体更新方法进行了改进，提出了变异概率的动态确定方法，利用骨折愈合实测应力曲线族，进行了骨折创伤断面最佳生理刺激应力的寻优，得到了理想的寻优结果.

1 骨折创伤断面生理刺激应力的寻优模型

骨折治疗的Jorgensen理论表明，采用骨外固定器固定后理想的骨折愈合曲线应呈双曲线变化，如图1所示.在此曲线中，骨折部位愈合组织的刚度随着外固定时间增长而迅速增加，以后呈持续缓慢增加，最后成渐进线而接近正常.

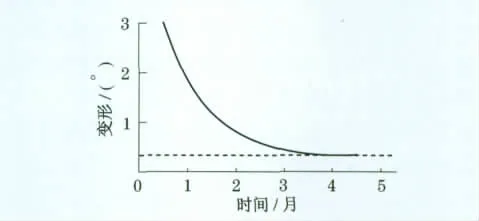
图1 骨折创伤断面应力变化的Jorgensen曲线Fig.1 Jorgensen curve of fracture traumatic section stress

根据骨折愈合的Jorgensen理论，为了保障骨折愈合的质量，提高骨折愈合的速度，骨折愈合过程中创伤断面的生理刺激应力必须符合Jorgensen曲线的变化趋势，理论上应满足双曲线变化规律.因此，本文提出骨折愈合中创伤断面的最优生理刺激应力的解析表达式为

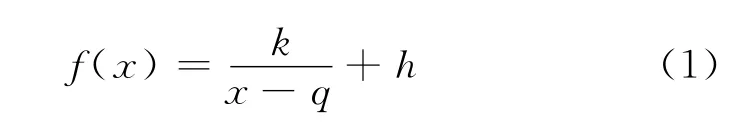
式中，q，h，k为寻优模型的待定常数；x为愈合时间；f（x）为愈合过程中创伤断面的应力.

在获得骨折愈合过程中创伤断面实测应力变化曲线族的条件下，可通过优化算法对q，h，k进行寻优，确定出创伤断面的最优生理刺激应力曲线.定义应力寻优的目标函数

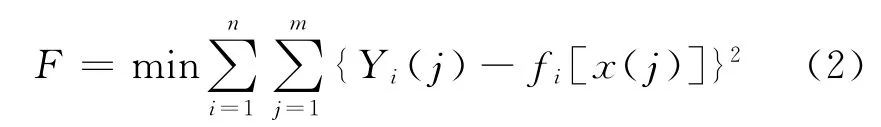
式中，Yi（j）为骨折创伤断面的实测应力数据序列；n为实测应力变化曲线的个数，即曲线族中应力曲线的个数；m为每条实测应力曲线中应力采样点的个数.

寻优的目标是使式（2）的目标函数最小.

2 改进的免疫遗传算法

2.1 免疫遗传算法的改进

本文提出的改进免疫遗传算法，主要针对普通免疫遗传算法中的抗体更新及交叉变异这两个重要步骤中的相关问题进行改进.

a.抗体更新.普通免疫遗传算法是借鉴生物免疫系统中抗体浓度控制原理提出的一种进化算法，它通过引入生物免疫系统中的抗体多样性、自我调节能力及免疫记忆能力等免疫特征之后，使算法吸纳了全局搜索能力、局部搜索能力及搜索速度等方面的优点.在普通免疫遗传算法中，抗原对应为优化目标，抗体对应为最优解集，抗体与抗原之间的亲和力对应为最优解集与优化目标函数之间的结合度.普通免疫遗传算法在抗体更新中通过计算每个抗体的相似度和浓度，判断抗体浓度是否超过设定阈值ε，计算超过阈值ε的抗体亲和力，再根据亲和力大小的排序来进行抗体更新.这种抗体更新方法保留了相似抗体中亲和力最大的抗体到下一代，它虽然可以防止优化过程陷入局部最小值，但会大大减少相似抗体中亲和力较低但基因模式较好的抗体，影响了优化算法对全局最优解的挖掘.针对该问题，本文提出在抗体更新步骤中通过计算种群总体相似度，判断其是否超过设定阈值θ，在超过阈值θ的种群中计算抗体浓度和亲和力，最终根据亲和力大小的排序来进行抗体更新.这种改进不再简单地通过判断某个抗体的浓度，而是从总体上判断种群总体的相似度来调节种群的多样性.抗体种群总体相似度大，说明此时种群中的模式种类较少；反之，相似度较小时，说明种群中具有多种模式，满足种群在进化过程中种群模式的多样性要求.

本文采用信息熵作为评价抗体相似度的指标.

定义1 假设种群中包含N个抗体，每个抗体具有M个基因，每个基因有s个字符可供选择.对于十进制编码，s＝0，1，…，9，即采用0～9的字符；对于二进制编码，s＝0，1，即采用0，1字符.根据信息熵理论，第j个基因的信息熵可表示为

式中，pij为第j个基因座上出现第i个字符的概率，整个群体的平均信息熵可定义为

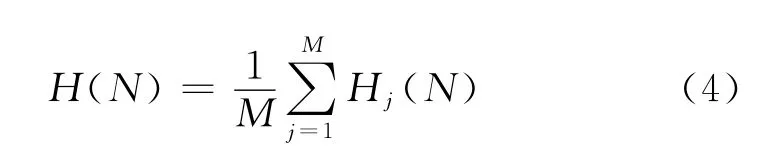
式中，Hj（N）为第j个基因座的信息熵；H（N）为抗体在种群中的平均信息熵.

两抗体v，w的相似度可以表示为

式中，Hv，w（2）为抗体v，w的信息熵；Av，w∈［0，1］.

Hv，w（2）＝0，说明抗体v，w的所有基因完全一致，相似度Av，w＝1.

定义2 抗体浓度表示的是相似抗体的个数占抗体总数的比例，任意抗体v的浓度Cv可表示为

式中，sign（·）为符号函数；μ为相似度系数，μ值范围为［0.9，1］.

定义3 亲和力是指抗体与抗原之间的结合程度.对于实际优化问题，如果优化目标函数为求最大值，则将亲和力表示为目标函数的值；反之，若优化目标函数为求最小值，则亲和力表示为目标函数的倒数.对于式（2）所表示的优化目标，将亲和力定义为

式中，F为优化目标函数；Xv为解码之后得到的实数解向量.

定义4 使用抗体种群总体相似度作为抗体更新的依据时，抗体种群总体相似度定义为

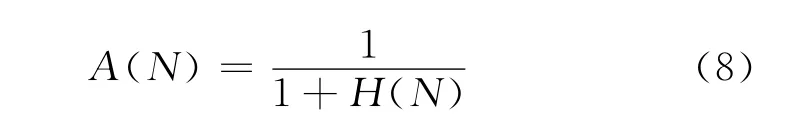
式中，H（N）由式（4）计算.

b.动态变异概率.普通免疫遗传算法中，变异概率需预先设定，且在整个优化过程中为定值.事实上，在寻优过程中，免疫遗传算法对变异概率的要求是不一样的.若抗体种群总体相似度超过设定阈值θ，则在下一代进化过程中需加大变异概率；反之，则应采用初始设定的变异概率.变异概率的确定对遗传算法的优化性能和收敛速度至关重要.若变异概率过小，会导致算法对种群新模式的开发力度不够，算法的优化性能变差；变异概率过大，算法操作随机性增大，会降低算法的收敛速度，甚至会导致优化算法的发散.针对该问题，本文提出一种如式（9）所示的变异概率的动态确定方法.

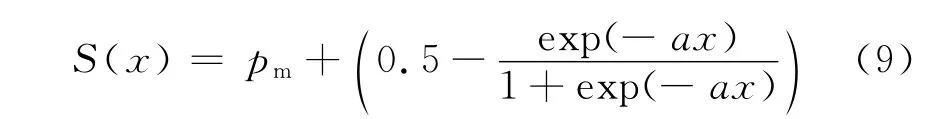
式中，pm为免疫遗传算法初始设定的变异概率；a为常数，其值对优化结果影响不大；x为根据式（8）计算的抗体种群总体相似度A（N）与设定相似度阈值θ之差.

若x≤0，则变异概率为初始变异概率pm；若x＞0，则按式（9）确定动态变异概率.由式（9）表示的变异概率的动态变化过程如图2所示.

图2 动态变异概率变化曲线Fig.2 Curve of dynamic mutation probability

从图2可以看出，当x≤0时，动态变异概率S（x）＝pm；当x＞0时，随着x的增大，变异概率的增长率却在逐渐减小，并逐渐趋于0，即变异概率增长到一定程度后将不再增大.按这种方法所确定的动态变异概率可以保证在抗体种群总体相似度超过设定阈值θ时的初期，能够快速地加大变异概率，使得种群模式的多样性得到快速的改善，减少陷入局部最小值的可能性.而当变异概率增大到一定程度时则减小变异概率变化的幅度，以保证算法不会因变异概率过大而影响算法的收敛或导致算法的发散.

2.2 改进免疫遗传算法的步骤

改进免疫遗传算法分编码、初始抗体生成、记忆池更新、交叉与变异、抗体更新等主要步骤.

a.编码.在骨折愈合最优应力曲线的寻优中，由式（1），需要优化确定的参数为3个，即q，h，k.采用二进制编码方式，若参数编码长度为l，长度l可以根据参数变化范围与设定的优化计算精度确定.

式中，x1，x2分别为优化参数变化范围的下限和上限；α为设定的求解精度.优化时3个优化参数的编码结构可以表示为其中，l1，l2，l3分别为根据式（11）计算出来的3个参数q，h，k对应的编码长度.

b.初始抗体生成.记忆池是有效抵抗抗原保留下来的免疫记忆细胞群，在免疫遗传算法中相当于此前优化处理过的案例库.当记忆池受到抗原刺激后能产生相应的抗体，抵抗抗原的入侵，因此，记忆池的存在能够加快优化算法的收敛速度.如果是对抗原的初次应答，即没有处理过相关的优化问题，则根据给定的抗体数量N以及编码总长度L＝l1＋l2＋l3，随机产生全部初始抗体种群RN×L，此时记忆池为空集.如果不是对抗原的初次应答，则初始抗体种群由随机产生的部分抗体和由记忆池产生的抗体组成，且抗体种群的规模为N.

c.更新记忆池.计算抗体浓度与抗体亲和力，按照亲和力排序，选择亲和力较高的抗体补充到记忆池里.

d.交叉与变异操作.

（a）交叉.交叉操作是将父代中的特性基因遗传给子代，使子代具有父代的优良信息.本文采用单点交叉，根据交叉概率随机从群体中选出两抗体A和B进行配对，在配对的抗体编码串中随机设置交叉点，交叉操作原理如图3所示.在图3中，A，B为父代抗体，A′，B′为交叉操作后生成的子代抗体.

图3 单点交叉示意图Fig.3 Diagram of single－point crossover

（b）变异.变异操作为优化过程提供了额外的机会进入未被探索的局部最优解区域，此操作能够加速优化过程向最优解收敛.根据变异概率，随机选择某个基因位进行变异操作，采用二进制编码时，具体操作为：假设变异概率为S（x），则某个基因位变异的表达式为

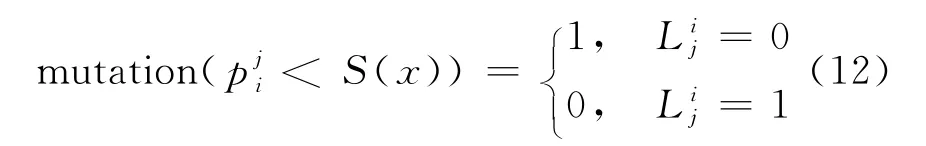
e.抗体更新.根据式（8）计算抗体种群总体相似度，如果相似度小于设定阈值θ，即A（N）≤θ，则转到步骤c；如果大于设定阈值θ，即A（N）＞θ，则随机生成P个新抗体，与原有抗体种群组成新的抗体种群B，新种群B的规模为N＋P.此时根据式（9）计算出新的变异概率S（x），用于下一代变异操作，并计算B中抗体的浓度和亲和力，按照亲和力大小排序.如果每个抗体的浓度都小于设定阈值ε，则直接清除亲和力排在最后的P个抗体；否则，在抗体浓度超过阈值ε的抗体中，清除亲和力较小的抗体直至保证抗体总数为N.

f.终止条件判断.本文的终止条件是迭代次数是否达到设定的最大值.如果迭代次数小于设定的最大迭代次数，则算法迭代继续进行；否则，迭代过程结束，输出优化结果.

3 骨折创伤断面最佳生理刺激应力寻优

文献［1－2］采用自行研制的带微型力传感器和施力机构的骨外固定器，采用骨外固定方式，设计活体骨折模型，进行活体山羊骨折愈合的动物实验，获得了多组活体山羊骨折愈合过程中创伤断面的应力－愈合时间变化关系曲线.基于这些应力数据族，本文分别采用改进免疫遗传算法、普通免疫遗传算法和标准遗传算法，根据式（1）的寻优模型和式（2）的优化目标函数，对骨折创伤断面的最佳生理刺激应力进行寻优.为了验证本文优化算法的有效性，本文采用文献［5］中第1组和第2组山羊股骨骨折创伤断面的实测应力曲线族，比较3种算法的寻优性能.

优化过程中优化算法的相关参数设置为：种群规模50，交叉概率0.8，初始变异概率0.05，抗体种群总体相似度设定阈值0.1，抗体浓度设定阈值0.3，最大迭代次数100，式（11）中的α为200.图4（a）、4（b）、4（c）为基于文献［5］中第1组实测应力数据族，分别采用本文优化算法、普通免疫遗传算法、标准遗传算法的目标函数变化曲线，图4（d）、4（e）、4（f）分别为采用3种优化算法的最佳生理刺激应力的寻优结果.图5为采用本文优化算法优化过程中变异概率的动态变化曲线.

本文优化算法得到的q，h，k值分别为0，0.261 4，0.506 8，根据式（2）计算得到的误差平方和为0.522 54；采用普通免疫遗传算法得到的q，h，k值分别为0.000 1，0.260 7，0.512 3，根据式（2）计算得到的误差平方和为0.528 18；采用标准遗传算法计算得到的q，h，k值分别为 0.004 15，0.261 37，0.544 51，根据式（2）计算得到的误差平方和为0.556 03.

从图4及优化结果可知，使用本文提出的改进免疫遗传算法时，寻优在20～30代时算法几乎已经达到最优值，而普通免疫遗传算法在40～50代时才能接近最优值，采用标准遗传算法则需要在60～80代才能接近最优值，且采用本文优化算法获得的优化曲线最接近于实际应力变化曲线族.

图4 第1组应力变化曲线族的优化过程及其优化结果Fig.4 Optimization process and results of the first group of stress curve family

图6（a）、6（b）、6（c）为基于文献［5］中第2组实测应力数据族，分别采用本文优化算法、普通免疫遗传算法、标准遗传算法的目标函数变化曲线，图6（d）、6（e）、6（f）分别为采用3种优化算法的最佳生理刺激应力寻优结果.图7为采用本文优化算法优化过程中变异概率的动态变化曲线.

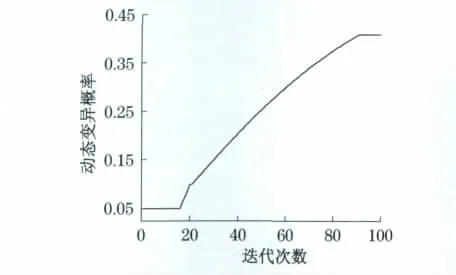
图5 第1组优化过程中变异概率的动态变化曲线Fig.5 Curve of dynamic mutation probability in the first group optimization

本文优化算法得到的q，h，k值分别为0，0.328 4，0.930 9，根据式（2）计算得到的误差平方和为0.302 53；采用普通免疫遗传算法得到的q，h，k值分别为0.000 1，0.312 5，1.025 3，根据式（2）计算得到的误差平方和为0.308 18；采用标准遗传算法计算得到的q，h，k值分别为0.041 5，0.375 2，0.761 0，根据式（2）计算得到的误差平方和为0.318 03.

从图6及优化结果可知，使用本文提出的改进免疫遗传算法时，寻优在10～20代时算法几乎已经达到最优值，而普通免疫遗传算法在20～30代时才能接近最优值，采用标准遗传算法则需要 在3 0～4 0代才能接近最优值，且采用本文优获得的优获得的优化曲线最接近于实际应力变化曲线族.

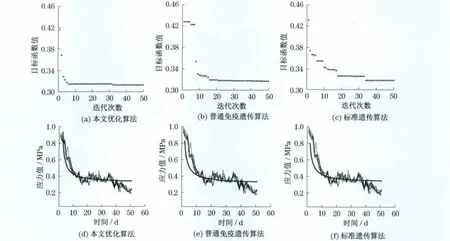
图6 第2组应力变化曲线族的优化过程及其优化结果Fig.6 Optimization process and results of the second group of stress curve family

从图5和图7中变异概率的变化曲线可以看出，本文提出的优化算法中变异概率能根据优化要求进行自适应调整，可防止优化初期算法陷入“早熟”，并能保证优化后期种群的多样性，提高了算法的收敛速度和优化精度.

综合以上优化实例，与普通免疫遗传算法、标准遗传算法相比，本文提出的改进免疫遗传算法具有更快的寻优速度和更高的寻优精度，由其确定的骨折创伤断面生理刺激应力具有较高的临床应用价值.

图7 第2组优化过程中变异概率的动态变化曲线Fig.7 Curve of dynamic mutation probability in the second group optimization

4 结 论

a.针对普通免疫遗传算法存在的问题，提出了改进的抗体更新方法及动态变异概率的确定方法，提高了普通免疫遗传算法的优化性能.

b.基于山羊骨折创伤断面的实测应力变化曲线族，以骨折愈合的Jorgensen曲线为优化目标，提出了基于改进免疫遗传算法的骨折愈合过程中创伤断面最佳生理刺激应力的寻优方法，以提高骨折愈合的质量和速度.

c.基于实测应力数据的山羊骨折最佳生理刺激应力寻优结果表明，与普通免疫遗传算法和标准遗传算法相比，本文方法的寻优时间最短、寻优精度最高，获得了理想的寻优结果.

［1］朱坚民，翟东婷，黄之文.基于弱化缓冲算子和GM（1，1）等维新息模型的骨折愈合应力预测［J］.中国生物医学工程学报，2012，31（2）：268－275.

［2］缑冬青.骨折断面愈合应力实验分析与计算机仿真研究［D］.洛阳：河南科技大学，2003.

［3］Zhu Jianmin，Zhang Xiaolan，Wu Jingjing，et al.Prediction on stress during bone fracture healing based on equal－dimension and new－information model GM（1，1）［J］.The Journal of Grey System，2008，20（3）：187－194.

［4］Zhu Jianmin，Wang Jun，Lei Jingtao.Grey predictive control of stress on trauma section during union of fracture［J］.The Journal of Grey System，2011，23（1）：15－24.

［5］Zhu Jianmin，Zhu Huanghuang，Zhang Xiaolan，et al.A quantitative evaluation method for fracture union quality based on grey relational analysis［J］.The Journal of Grey System，2011，23（2）：127－134.

［6］张明明，赵曙光，王旭.基于Baldwin效应的自适应有性繁殖遗传算法及其仿真研究［J］.系统仿真学报，2010，22（10）：2329－2332.

［7］Saridakis E.Novel genetic algorithm－inspired concept for macromolecular crystal optimization［J］.Crystal Growth ＆ Design，2011，11（7）：2993－2998.

［8］Jahangirian A，Shahrokhi A.Inverse design of transonic airfoils using genetic algorithm and a new parametric shape method［J］.Inverse Problems in Science and Engineering，2009，17（5）：681－699.

［9］Fabio F，Maurizio R.Comparison of artificial immune systems and genetic algorithms in electrical engineering optimization ［J］. The International Journal for Computation and Mathematics in Electrical and Electronic Engineering，2006，25（4）：792－811.

［10］Salah S A，Duarte－Mermoud M A，Beltran N H.Probabilistic adaptive cross－over（PAX）：a novel genetic algorithm crossover methodlogy［J］.International Journal on Artificial Intelligence Tools，2008，17（6）：1131－1160.

［11］Wu A，Tsang P W M，Yuen T Y F，et al.Affine invariant object shape matching using genetic algorithm with multiparent orthogonal recombination and migrant principle［J］.Applied Soft Computing，2009，9（1）：282－289.

［12］柴永生，孙树栋，余建军，等.基于免疫遗传算法的车间动态调度［J］.机 械工程学报，2005，41（10）：23－27.

［13］陈文英，阎绍泽，褚福磊.免疫遗传算法在智能桁架结构振动主动控制系统优化设计中的应用［J］.机械工程学报，2008，44（2）：196－200.

［14］梁勤欧，周晓艳.基于免疫遗传算法的设备布局问题研究［J］.武汉理工大学学报，2011，33（4）：643－646.

［15］杨建华，孙 钢，吴朝晖.基于免疫遗传算法的卫星天线结构设计［J］.浙江大学学报（工学版），2010，44（4）：645－651.

［16］顾榕，曹立明，王小平.基于改进免疫遗传算法的交通信号优化控制［J］.模式识别与人工智能，2006，19（3）：331－337.

［17］Soroudi A，Ehsan M，Caire R，et al.Hybrid immunegenetic algorithm method for benefit maximisation of distribution network operators and distributed generation owners in a deregulated environment［J］.IET Gener Transm Distrib，2011，5（9）：961－972.

［18］Azimipour M，Bonyadi M R，Eshghi M.Using immune genetic algorithm in ATPG［J］.Australian Journal of Basic and Applied Sciences，2008，2（4）：920－928.

［19］Wang Dingwei，Fung R Y K，Ip W H.An immunegenetic algorithm for introduction planning of new products［J］.Computers ＆ Industrial Engineering，2009，56（3）：902－917.