金融市场风险测量模型的计算方法研究与比较

刘红玉

(1.陇南师范高等专科学校，甘肃 成县 742500;2.兰州大学，甘肃兰州 730000)

金融市场风险，指金融资产的市场价格变化或波动而引起的未来可能损失，是各经济主体所面临的主要风险之一。基于市场价值测量法(Mark to Market)的风险价值方法(Value at Risk，VaR)，成为金融市场风险测量的主流方法。研究VaR方法的理论基础和实证技术，对于金融风险管理的有效性及合理性，回答风险管理最关心的两大问题:损失的大小和发生损失的可能性，具有重要意义。很多金融风险管理的思想、理论和模型都是围绕VaR建立展开的。

一、VaR的定义

根据Jorion(1996)给出的权威定义，VaR指的是在一定概率水平下(置信度)，某一金融资产在未来特定的一段时间内的最大可能损失。更严格地说，VaR描述了一定的目标期间内收益和损失的预期分布的分位数。用数学公式表示为:Prob(△p＞VaR)=1－c

其中△P为证券组合在持有期△t内的损失，c为预先给定的置信度，VaR值为置信水度c下处于风险中的价值。

VaR的数值取决于三个因素:(1)置信度的大小;(2)持有期的长短;(3)金融资产或证券组合未来损益分布的特征。

二、VaR△计算的基本原理

(一)一般分布下的计算

设一投资组合初始价值为P0，R是持有期内的收益率，则组合的期末价值为P=P0(1+R)。假定回报率R的期望值为μ，波动率为σ，给定置信水平c下组合的最低价值为P*=P0(1+R*)，那么根据定义在该置信水平c下，投资组合在未来持有期L内的相对VaR值可定义为:VaR=E(P)－P*=－P0(R*－μ)

绝对 VaR值可定义为:VaR = P0－P*=－P0R*

由此可知，计算VaR△μ相当于计算组合最小价值P*或最低收益率R*。假定组合未来收益率分布的概率密度函数为f(P)，则对于置信水平c下组合的最低值P*有:

(二)参数分布下的VaR计算

如果分布假定属于参数分布类，如正态分布，则VaR的计算可大大简化。在这种情况下，使用一个依靠置信水平的多样性因素，VaR可直接由投资组合的标准差的给出。该方法有时被称为参数法(parametric)，因为他包括参数的估计值，如标准差而不是从经验得到的分布中求分位数。

如果投资组合的收益率分布为正态分布，若标准正态分布的密度函数为Φ(ε)，则有:

其中α(α＞0)为指定置信水平c下标准正态分布的分位数，公式表示为:

由此可得最小回报率R*为:R*=μ－ασ

在标准正态分布下，置信水平与分位数一一对应。当给定一个置信水平如95% 时，则对应分位数α=1.65，于是就可以计算出相应的R*和VaR值。以上计算都是基于一天的时间间隔基础上的，如果要计算持有期长度为△t的VaR值，假设连续时间区间的收益率不相关，则时间间隔为△t的相对VaR值为:V

三、VaR计算的主要方法

VaR的计算有多种方法，适应于不同的市场条件、数据水平、精度要求等，根据是否利用投资组合收益率分布的参数来计算投资组合VaR。不同的波动性模型和估值模型构成了VaR计算的不同方法。

(一)历史模拟法

历史模拟法是一种简单实用的方法。该方法不需要对损益分布作出任何假定，完全依赖于历史数据，并假定市场未来的发展是具有延续性的。其核心在于用给定历史时期上所预测到的市场因子的波动性，来表示市场因子未来变化的波动性。

1.历史模拟法主要计算步骤

第一、映射，即首先识别出基础的市场因子，收集市场因子适当时期的历史数据(典型的是到年的日数据)，并用市场因子表示出证券组合中各个金融工具的盯市价值(对于包含期权的组合，可使用Black－Schole或Garman－Kohlhagen公式计算);第二、根据市场因子过去N+1各时期的价格时间序列，计算市场因子过去N+1个时期价格水平的实际变化(得到N各变化水平)。假定未来的价格变化与过去完全相似，即过去N+1个时期价格的N个变化在未来都可能出现，这样结合市场因子的当前价格水平可以直接估计(模拟)市场因子未来一个时期的N种可能价格水平;第三、利用证券定价公式，根据模拟出的市场因子的未来N种可能价格水平，求出证券组合的N种未来盯市价值，并于当前市场因子的证券组合价值比较，得到证券组合未来的N个潜在损益——损益分布;第四、根据损益分布，通过分位数求出给定置信度下的VaR。

这种方法由于采用市场因子的历史价格模拟其未来的的可能价格水平，因此称为历史模拟法。

2.历史模拟法法的优点:

(1)计算简单方便。(2)不需要对收益率的分布做出假设。(3)历史模拟法无需估计波动性、相关性等各种参数，也就没有参数估计的风险;历史模拟法不需要市场动态性模型，因此避免了模型风险。(4)历史模拟法是全值估计方法，可以较好的处理非线性、市场大幅波动的情况，捕捉各种风险，更重要的是历史模拟法考虑了厚尾问题。

(二)基于核估计的历史模拟法

基本思想:首先，用非参数方法估计组合回报的概率密度函数和累积概率密度，也称为高斯核估计;其次，求得回报分布的各阶统计量的概率密度;最后，由于该概率密度函数不是通过分析方法得到的，所以可以使用高斯的Legendre积分来得到次序统计量概率密度函数的各阶矩，均值就是所求的VaR估计，方差就是VaR估计的标准误差。

(三)蒙特卡罗模拟法(Monte Carlo)

Monte Carlo模拟法(简称MC)是一种随机模拟方法，它用市场因子的历史波动参数产生市场因子为来波动的大量可能路径(而历史模拟法只能根据市场因子的特定历史变动路径产生有限的未来波动情景)。虽然正态分布是MC中最常用的分布假定，但MC无须假定市场因子服从正态分布。

1)Monte Carlo模拟法的基本步骤如下:①针对实际问题建立一个简单且便于实现的概率统计模型，使所求的解恰好是所建模型的概率分布或其某个数字特征，比如，是某个事件的概率，或者该模型的期望值;②对模型中的随机变量建立抽样方法，在计算机上进行模拟试验，抽取满足的随机数，并对有关的事件进行统计;③对模拟试验的结果加以分析，给出所求解的估计及其精度(方差)的估计;④必要时，还应改进模型以提高估计精度和模拟计算的效率。

2)Monte Carlo模拟的优点:

(l)可产生大量情景，比历史模拟法更精确和可靠;(2)是一种全值估计方法，可以处理其他方法所无法处理的风险和问题，如非线性价格风险、波动性风险、粗尾分布、极端事件甚至信用风险，它都能有效地处理;(3)可模拟收益的不同行为(如白噪声、自回归和双线性等)和不同分布。

(四)RiskMetrics方法

JP Morgan于1994年提出RiskMetrics的模型是基于EWMA模型基础上的，赋予近期数据较高的权重，反映出了波动性的动态特征，并且能较快地反映市场冲击。冲击发生后，随着权重的减小，波动性呈指数形式衰减。实际操作中，JP Morgan的RiskMetrics系统是通过最小化平方根的平均误差来确定λ的值。设σ2t+1|t是对r2t+1的无偏估计，即E(r2t+1)=σ2t+1|t，估计误差为 ξt+1|t= r2t+1－ σ2t+1|t，那么有E(ξt+1|t)=E(r2t+1)－ σ2t+1|t=0

RiskMetrics方法是VaR计算的一种比较简单的方法，关键因素在于:组合价值函数的估计方法;市场因子服从的分布形式。采用移动平均方法中指数移动平均模型预测波动性。它假定过去的回报分布可以合理的预测未来情况，可用历史数据的时间序列分析估计市场因子的波动性和相关性。RiskMetrics假定市场因子变化服从正太分布。

(五)GARCH模型

Engle在1982年首先提出了ARCH模型对方差进行建模;1986年Bollerslev将ARCH模型推广，发展成为广义的ARCH模型，即GARCH模型。随后的十几年中，计量经济学家对基本的GARCH模型进行许多变形，现在一发展成为一个包含众多方法的模型类型。大量实证研究表明，GARCH类模型特别适合于对金融时间序列数据的波动性和相关性进行建模，估计或预测波动性和相关性。GARCH用于对市场因子波动的条件异方差性建摸，它可以更好地预测市场因子的真实波动性，如波动性集聚效应。虽然GARCH最常用是正太分布，但也可以采用其他分布假定。

(六)利用极值理论计算

无论是半参数模型还是完全参数模型，计算的都是概率较大的分位数，这对于回报分布的上尾部，但VaR值是在回报分布的下尾部，因此需要对样本数据做一个变换。

用St表示某资产在第t天的价格，rt表示其对数回报，则

为了计算回报分布的下侧分位数，对样本数据取负数，即Xt=－rt。于是通过Xt计算得到的上侧分位数再取负号就是所求VaR的值。包括基于无条件极值分布的VaR估计、基于条件极值分布的VaR估计和基于条件极值分布的VaR估计模型与其他模型的比较与检验等。

(七)混合方法

基于极值理论的VaR计算方法与VaR其他计算方法相结合，以便在各种概率条件下都能准确地估计VaR值。最为典型的方法就是混合方法。主要有历史模拟法与极值理论的混合方法;RiskMetrics与极值理论的混合方法等。

四、的计算方法比较

既然计算VaR有如此多种不同的方法，具体应用时应该选择哪一种方法来计算呢?这要根据证券投资组合中是否包含大量的期权或隐含期权的金融工具、数据收集的状况、方法实现的难易程度、计算的速度、向高层管理者解释的难易程度、主要缺点、VaR的精确性与分析等条件来决定。表描述了各种方法的优劣。

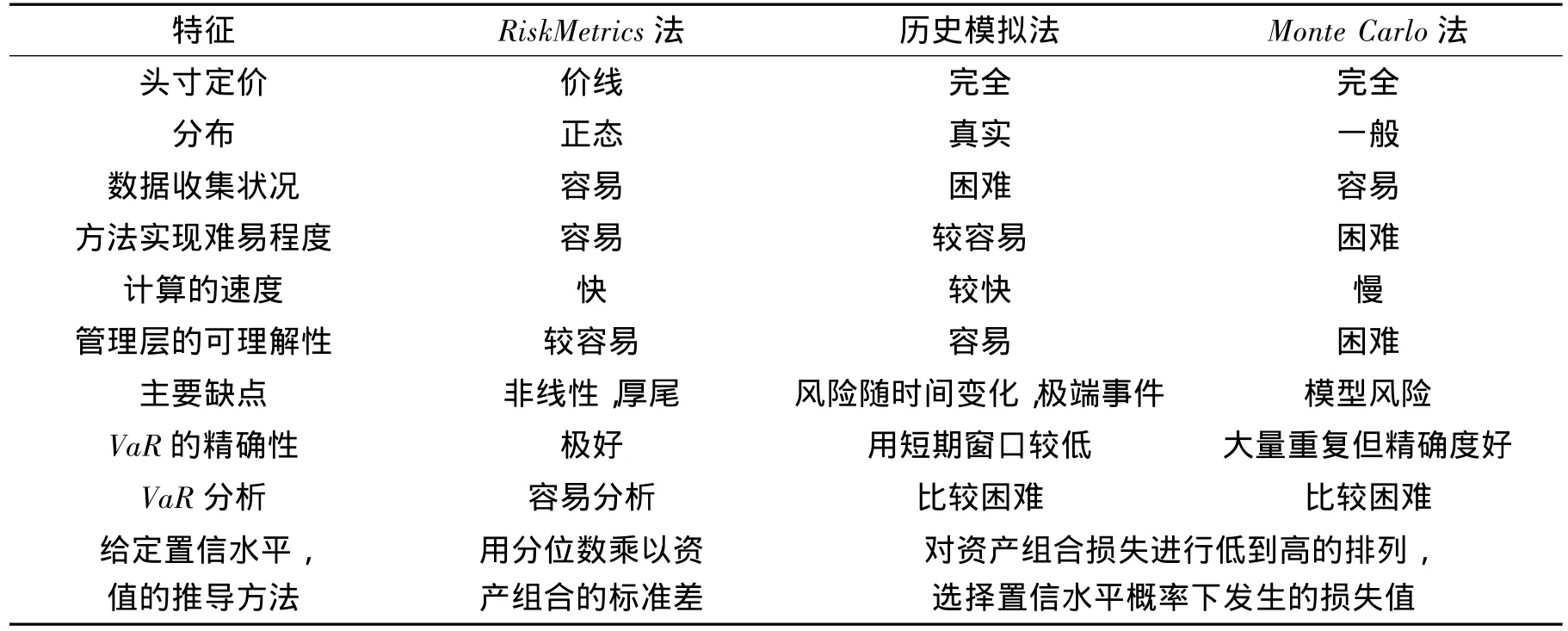
VaR计算方法的比较

另外，国内外对于VaR的研究仍有待进一步丰富和完善。第一，研究计算方法的选择。国内外对于经典VaR计算方法中方差——协方差法和Monte Carlo模拟法研究得非常多，而对历史模拟法研究得相对较少。国外极值理论的研究最近几年比较兴盛，而国内的类似文献要少得多。第二，VaR的应用。国外研究者多着眼于VaR作为风险计量和市场风险监管的作用，而国内大量文献对VaR方法在绩效评估、投资组合优化、金融机构竞争力评价体系的构建等方面的作用表现出更多的兴趣。第三，对各种计算方法关系的认识以及派生的研究取向的分歧。至少并无任一有说服力的文献可以证明经典VaR计算方法体系中的三大方法存在着绝对的优劣区别。因此，与许多学者一样，主张应该着力于探索各个方法之间应如何借鉴彼此优点。

VaR方法是一种既能处理非线性问题又能概括证券投资组合市场风险的工具，它解决了传统风险定量化工具对于非线性的金融衍生工具适用性差、难以概括证券组合的市场风险的缺点，有利于测量风险、将风险定量化，进而为金融风险管理奠定了良好的基础。

［1］ Jorion P.Value at risk:The new benchmark for controlling market risk.New York:The McGraw － Hill Companies，Inc，1997.

［2］ 秦拯，陈收，邹建军.的计算方法及其评价［J〕.系统工程，2005(7):8－11.

［3］ 黄海，卢祖帝.主要计算方法评述［J］.金融管理，2003(7):31－36.

［4］ 徐钟济.蒙特卡罗方法［M］.上海:上海科学技术出版社，1985.

［5］ Engle R F.Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdominflation.Econometrica，1982，50(4):987 －1007.

［6］ Bollerslev T.Generalised autoregressive conditional eteroskedasticy .Journal of Econometrics，1986(31):307 －327.

［7］ 王春峰.金融市场风险管理［M］.天津:天津大学出版社，2001.

［8］ 陈守东，王鲁非.与其他风险度量指标的比较［J］.经济题，1997(5):18－23.