递减法求解湿球温度

李志龙，谷洪钦，徐兆斌，战祥伦

(国核电力规划设计研究院，北京 100095)

1 概述

湿球温度是工程设计中常用的气象要素之一，如火力发电工程的10%气象条件，一般根据最近五年最炎热三个月的逐日平均湿球温度求得。由于目前很多气象站没有直接观测湿球温度，而是采用干球温度、相对湿度、水汽压、大气压等其它气象要素值，由“湿度查算表”查取。

通过“湿度查算表”查取湿球温度的方法效率较低，且容易出错，当数据较多时，宜采用计算机进行批量计算。目前计算湿球温度的方法主要有试错法和迭代法两种，两种方法的最终计算结果并没有原则差异，主要是运算次数的差别。本文通过论证饱和水汽压与湿球温度的函数单调性，提出计算湿球温度的新方法，并论证了固定步长和变步长两种发式的运算效率。

2 基本原理

空气中的水汽压可用下式表示：

e为水汽压，单位hPa； Etw为湿球温度tw对应的纯水平液(冰)面饱和水汽压，单位hPa； A为干湿表系数，单位℃-1，当湿球未结冰时，可取0.000667℃-1，当湿球结冰时，可取0.000588℃-1； Ph为气压，单位hPa； t为干球温度，单位℃； tw为湿球温度，单位℃。

Etw可采用戈夫-格雷奇(Goff-Grattch)饱和水汽压公式计算，该公式自1947年起就为世界气象组织(WMO)推荐公式，是以后多年世界公认的最准确的计算公式，也是我国湿度查算表中所采用的公式。

纯水平液面饱和水汽压(温度范围-49.9℃～+49.9℃)：

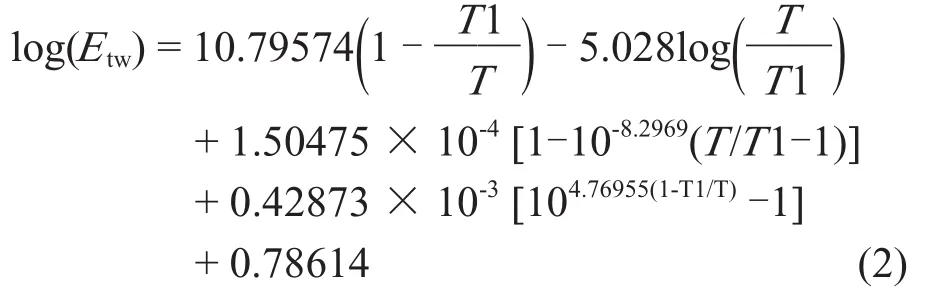
纯水平冰面饱和水汽压(温度范围-79.9℃～-0.0℃)：

其中T1= 273.16 ºK(水的三相点温度)，T=273.15 + tw℃(绝对温度)。通过(1)和(2)式或(1)和(3)式即可确定湿球温度，但由于函数比较复杂，很难直接求解。

3 递减法基本原理

3.1 Etw～tw函数单调性

根据(2)式和(3)式，饱和水汽压与湿球温度函数关系曲线见图1(a)和(b)。

图1 饱和水汽压～湿球温度关系曲线

根据(2)式和(3)式，分别对tw求导，纯水平液面和纯水平冰面求导结果分别为(4)式和(5)式。

对于(4)式，由于223.25≤T≤323.05，则2949/T-2.18>0，得∂EEtw/∂Etw>0；对于(5)式，193.25≤T≤273.15，则1.55/T-0.0032>0，得∂EEtw/∂Etw>0。因此，对于纯水平液面和纯水平冰面情况下，饱和水汽压随湿球温度均呈单调递增变化。

3.2 递减法求解

根据(1)式得t - tw =(Etw- e)/(A·Ph)≥0，即tw≤t，湿球温度小于或等于干球温度。

将(1)式化为e+ A·Ph·t = Etw+ A·Ph·tw，由于左侧e+ A·Ph·t 为定值，右侧Etw随tw单调递增，可知Etw+ A·Ph·tw随tw单调递增，且tw≤t。因此，只要把干球温度作为初始值，设定合适的步长和精度，逐次递减试算即可求出tw。

例如：某气象站实测干球温度11.3℃，气压884.2hPa，水汽压10.2hPa。则e + A·Ph·t等于16.8，即Etw+ A·Ph·tw=16.8。设初值tw =11.3℃，步长为0.1℃，精度为0.1，通过逐步递减tw求算得湿球温度为9.0℃，由“湿度查算表”查取校正值，即可得到最终的湿球温度，试算过程见表1。

表1 湿球温度试算

3.3 变步长计算

采用固定步长进行递减计算，最大计算次数取决于干湿球温差与步长的比值。由于精度要求，步长一般远小于干湿球温差，所以计算次数较多。为缩减计算次数，可采用变步长的方法：假设初始步长为l，初始湿球温度为tw =t- l，当(Etw+ A·Ph·tw)-(e+ A·Ph·t)>0，则保持步长不变，湿球温度为tw =tw-l，直至(Etw+ A·Ph·tw)-(e+ A·Ph·t)<0；确定了湿球温度范围后，开始变步长，步长缩小为l = l/2，tw=tw+l，如(Etw+ A·Ph·tw)-(e+ A·Ph·t)>0，则l = l/2，tw =tw-l，如(Etw+ A·Ph·tw)-(e+A·Ph·t)<0，则l = l/2，tw =tw+l，如此循环，直至(Etw+ A·Ph·tw)-(e+ A·Ph·t)= 0。

3.4 结果分析

采用固定步长方式，计算次数取决于干湿球温差与步长的比值，出于精度的要求，步长一般取0.1℃，则试算次数为(t - tw)/l = 10(t -tw)，即干湿球温差的10倍。

采用变步长方式，最大计算次数分为两部分：一为固定步长部分，计算次数为INT[(t- tw)/l]+1，取决于干湿球温差和初始步长的比值；二为变步长部分，计算次数为INT[ln10/ln2]+1，取决于初始步长。干湿球温差和初始步长与计算次数关系见表2。由表2统计结果显示，初始步长大于3℃后，计算次数非常稳定，且基本不受干湿球温差影响，最大计算次数稳定在8～9次。

表2 干湿球温差、初始步长和计算次数关系

根据上述分析结果，采用变步长方式计算次数稳定且远少于固定步长。例如：某气象站2006～2008年夏季逐日平均干湿球温差6.5℃，最大13.1温差℃，最小温差1.0℃。采用固定步长的方法平均试算65次，最多131次，最少10次；采用变步长的方法，初始步长取6℃，平均试算7次，最多9次，最少1次。

4 结论

通过论证饱和水汽压与湿球温度的函数单调关系，探讨湿球温度计算的新方法——

递减法，并论证了采用固定步长和变步长方式的计算次数。该方法计算原理简单，易于理解，采用变步长方式计算次数只跟初始步长有关，不受干湿球温差影响，计算次数少且稳定。

[1]国家气象局.湿度查算表[M].北京：气象出版社，1986.

[2]吕国义，陈勇.湿度换算软件包在干湿球温湿度计算中的应用[J].郑州轻工业学院学报(自然科学版)，2004，19(4).