基于1-分类支持向量机的机器视觉缺陷分类方法
李 琪, 卢荣胜, 陈 成
(合肥工业大学 仪器科学与光电工程学院,安徽 合肥 230009)
0 引 言
随着现代制造业的飞速发展,在一些高速连续的生产线上,如薄膜材料、纸张/出版物和带钢铝材的生产中,对产品的生产速度和表面质量要求都有了明显的提高,而在生产过程中由于原材料和生产过程的技术原因,都不可避免地会产生多种缺陷,传统上对这些缺陷检测常采用人工检测、检测式检测、电磁式检测和电涡流式检测等方法,但是这些方法效率低、劳动强度大、误检率高,对产品造成损伤或受限于检测材料的性质。随着现代生产技术的进步,这些方法已不适应检测要求。而机器视觉缺陷检测技术作为一种非接触、高效灵活、检测精度高、适用范围广的检测手段,得到了迅猛发展。目前影响力较大的有德国的Parsytec公司和美国的Cognex公司,它们针对钢材检测和纸张/薄膜检测分别推出了HTS/HTP和ISRA VISION表面缺陷检测系统,这些系统都采用CCD或CMOS相机作为光电接收装置,采用明场/暗场反射成像方式生成缺陷图像,并且将神经网络引入到缺陷检测过程中。目前,国内机器视觉检测还局限于小规模视场的在线检测。
机器视觉检测过程主要涉及对采集的图像进行预处理、缺陷分割和缺陷分类3个环节,其中图像预处理和缺陷分割属于数字图像处理的范畴,其研究已经十分成熟。而缺陷图像分类属于模式分类的范畴,它是将基于统计学习的理论引入到表面缺陷的自动分类中,对实现检测自动化具有十分重要的作用。模式分类源自机器学习方法是在给定样本数据集上,评估数据样本的内在概率联系,建立输入输出对应关系模型,并对新样本数据进行划分的过程。相比于神经网络方法,模式分类是建立在VC维和结构风险最小[1]基础上,而神经网络方法对网络结构的构建选择尚无完整的理论指导,因此模式分类对实际数据泛化能力和分类效果要更好。在模式分类中,目前最有前途的方法当属SVM支持向量机,一般情况下使用SVM方法时,首先为所有的缺陷类别都选取大致相等的缺陷训练样本,生成分类模型,然后将待测试的缺陷输入模型中,最后得到一个结果表明缺陷所属归类。但是在实际检测过程中,会遇到不同类缺陷的训练样本数目存在很不均衡的情况,此时仍使用多分类的方法会产生较大的分类误差。因此,针对这种情况研究基于1-分类的SVM方法,该分类方法只检测待测样本属于/不属于某一类缺陷,产生真/假的结果。
1 支持向量机原理
支持向量机分类模型有线性分类模型和非线性分类模型2种,线性模型是基础,非线性分类模型主要是由各种核函数与线性模型结合起来得到的;此外,SVM原型是2分类模型,多分类模型是在2分类基础上通过组合得到的[2]。
1.1 线性分类原理
在线性SVM中,假设分类特征是n维向量x=(x1,…,xn),则线性分类器定义为实值函数f:
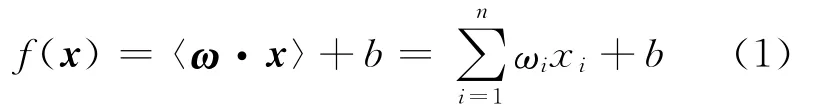
由(1)式可以看到f定义了一个由n维变量到1维变量的映射,其中n维变量代表输入样本特征,1维代表此样本所属类别的标签,并且这个函数是通过参数对(ω,b)∈Rn×R确定的。另外从几何角度解释,(ω,b)在特征空间中确立了一个线性划分超平面H:ω·x+b=0。对于2分类问题,超平面将n维输入空间X分为两半,对应于ω·x+b≥k1区域定义为正类,用yi=1表示;对应于ω·x+b≤k2区域定义为负类,用yi=-1表示,接着对超平面做变换,平移H,使得有ω·x+b′≥k和ω·x+b′≤k,不等式两边除以k,使得有ω′·x+b″≥1和ω′·x+b″≤1,最后就得到了线性SVM公式的标准形式,即

(2)式可以写成统一的形式,即yi(ω·x+b)≥1。使用SVM进行分类的第1步是对分类器进行训练,由(2)式可以看出SVM 的未知参数为(ω,b),因此训练过程实际上就是根据训练样本求得最优参数(ω,b)的过程。假设有训练集s={(x1,y1),…,(xi,yi)},其中xi是训练样本,yi是xi的已知分类标签。
此时由超平面几何距离可以求出最近样本点到超平面的距离为d=|ω·xi+b|/‖ω‖=1/‖ω‖,进而得到2类的分类间隔为2/‖ω‖。为提高分类准确率,要求2/‖ω‖尽可能大,该问题可变为求解约束优化问题,即
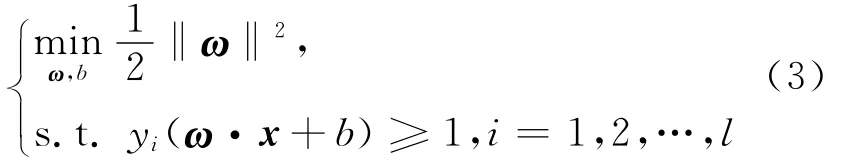
其中,ω为超平面系数向量;b为分类超平面阈值。为更进一步提高分类准确率,SVM还引入了松弛变量ξi≥0(i=1,2,…,l)和惩罚系数C,使得优化问题变为:
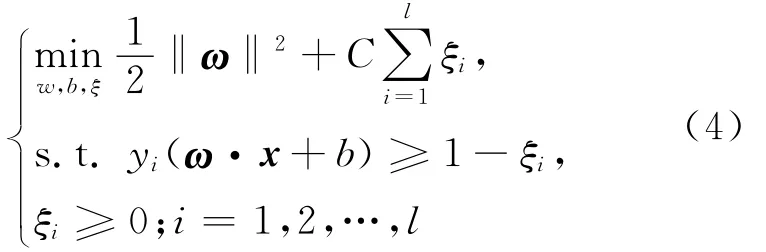
求解该优化问题采用拉格朗日乘数法,即
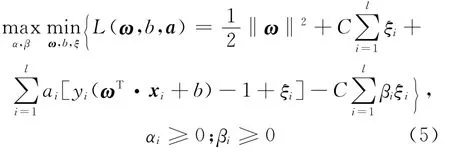
其中,αi和βi为拉格朗日乘子。(5)式分别对ω、b和ξ求导,并使之为0,可得:
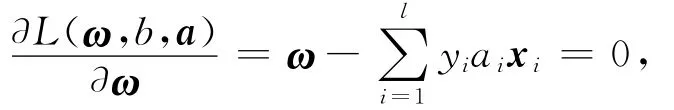
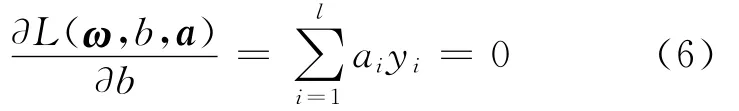
将(6)式代入到(5)式中,消去ω、b和ξ,即可得到原问题的对偶最优化问题:
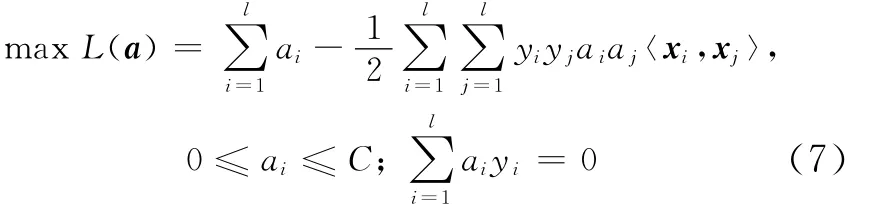
此时根据(7)式求解αi,其中与不为零的αi对应的xi即为分类器的支持向量,由支持向量得到最优超平面的ω和b。
1.2 非线性分类原理
非线性分类器对应于样本分类特征在特征空间中无法线性分类的情况,其思想是通过核函数将样本特征映射到高维特征空间,变换为线性可分的情况[3-4]。
核函数映射示意,如图1所示,图1b中一维空间内的2类缺陷无法进行线性分类,但是当将样本映射到二维空间时,就可以用线性分类的方法区分2类缺陷,如图1c所示。
研究的结果表明学生总体来说缺乏与策略相关的意识。他们相对来说缺乏丰富的策略储备,例如他们对学习策略不大了解。因此,他们不能实施恰当的学习策略和有意识的控制学习策略的使用[6]。所有这些都说明学生在不同的语言学习任务中实施恰当的学习策略以及控制策略使用方面的能力比较低。因此学习策略的培训也是迫在眉睫。学习策略的训练旨在帮助学习者考量影响自己学习的因素,找到最适合自己的学习策略,这样学习者才可能更有效的学习,并且对自己的学习负责。它更加关注的是学习过程,因此强调是如何学而不是学什么。因此高校应尽可能地为非英语专业大学生自主学习英语的过程中提供相应的帮助和指导,让学生掌握如何自主学习英语的能力。
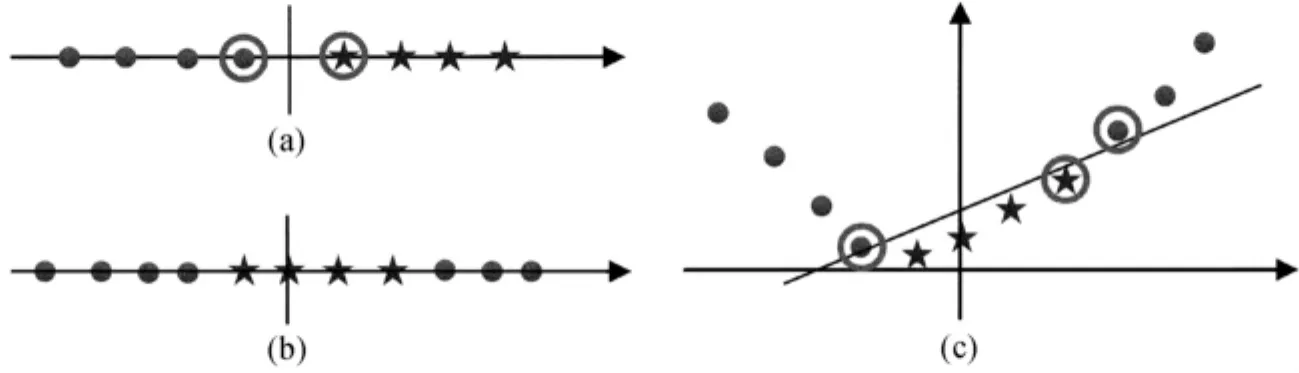
图1 核函数映射示意图
一般非线性SVM中的核函数有线性核函数、多项式核函数、径向基核(RBF)函数和Sigmoid核函数。
通常使用最多的为RBF函数,因为它的高斯径向基可以看作是无穷级数和,即可以将特征样本映射到无穷维的空间中,其表达式为:
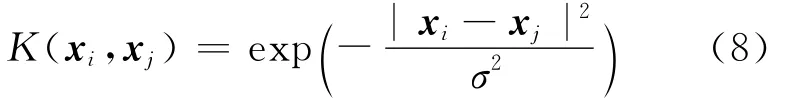
相应的求非线性最终化问题变为:
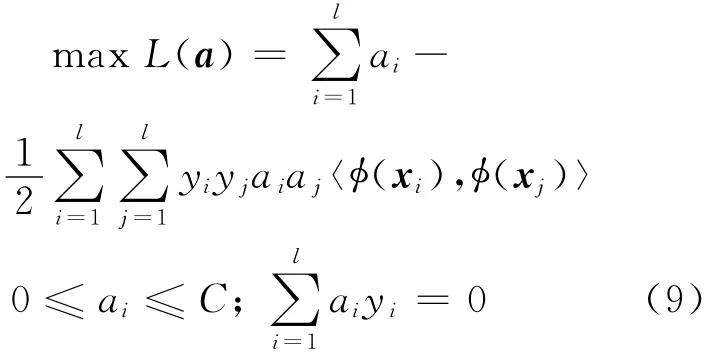
1.3 1-分类原理
在表面缺陷分类过程中,有时检测过程中会出现某些新类型缺陷需要分类判断,此时新类型缺陷样本数较少,且与其他类型缺陷的训练样本数目相比不均衡,这种情况如果仍然采用通常的SVM分类方法会对分类准确率造成较大影响。
1-分类方法的最小分类数为1,即判断待测试的特征向量“属于”或“不属于”某类,它只需要训练样本对特定类的特征向量分布有较好的描述,而不用关心训练集对其他类的特征向量分布的描述[5-8]。1-分类方法的优点是能够在缺少其他分类统计特征的情况下,对新的输入缺陷向量是否属于特定类进行精确判断,同时建立这种分类函数f(x:ω)需要的训练样本少,计算简单,分辨能力高。1-分类不同于其他SVM分类的超平面分类模型,它使用超球面作为分类边界,根据特定类的样本点计算超球面的球心和半径,并通过最优化问题求位置a和半径R的最小值。已知超球面表达式为:
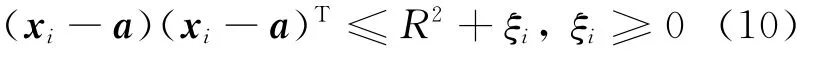
ξ为松弛变量,相应地用拉格朗日乘数法求解有:
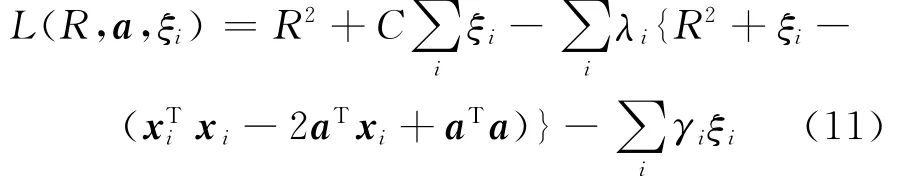
其中拉格朗日乘数λi≥0和γi≥0,对(11)式求R和a的偏导,可得:
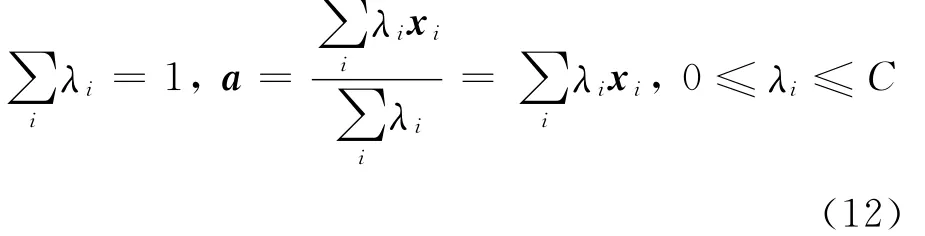
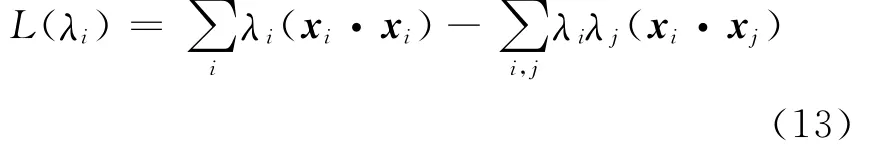
与线性SVM分类相似,可以将原问题转换为求对偶问题的极大值,求出λi的值,进而得到R和a的值。
在测试时,对于新的输入向量z,如果z在超球面内必须满足(14)式:
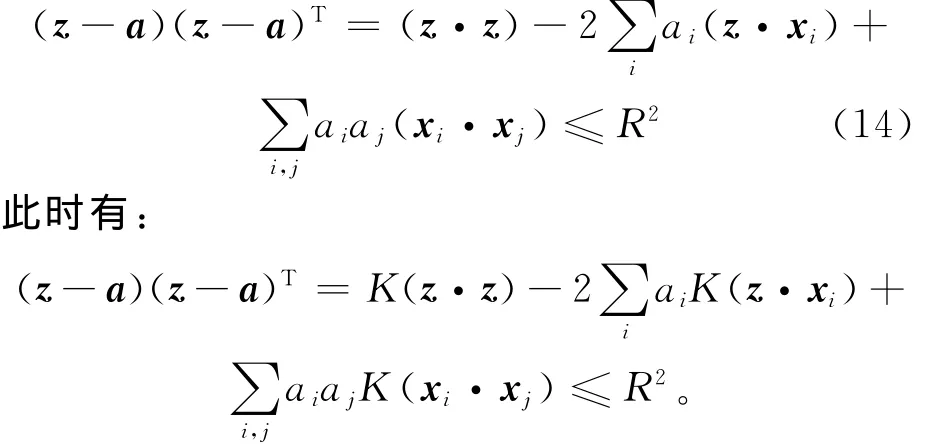
在表面缺陷检测的缺陷分类中,根据每种类型缺陷的训练集,使用1-分类方法得到N个超球面中心为as,半径为Rs:s={1,2,…,N}的分类函数fs,对一个新输入缺陷向量z,应用分类函数fs可以得到z点到不同球面中心的距离as,此时取距离中心点最短min(Rz)s时分类作为归属的类。
2 缺陷图像处理及特征参数选择
本文着重选取了孔洞、划痕和刮擦3种缺陷进行分类研究。
首先在预处理阶段,研究了傅里叶低通滤波、中值滤波、图像卷积滤波几种去噪方法,实验表明,中值滤波在计算速度和效果方面都有不错的表现。
其次在缺陷图像分割阶段,因为缺陷的几何形状差异很大,其中孔洞和划痕缺陷是连续区域缺陷,而刮擦缺陷是许多离散小区域缺陷,为正确将这些不同种类的缺陷在图像中分割出来,先通过设定阈值将图像二值化,同时创建一幅该二值化图像的副本。又因为缺陷区域为连续区域(孔洞和划痕)或许多相互间距离很近的离散小区域(刮擦),因此在副本图像中,用形态学中的闭操作将刮擦中的邻近离散小区域合并成一个大区域,接着搜索此时副本上的连通域,记录下每个连通域外接正方形的中心坐标和边长,最后返回到原始二值图像中,根据存储的中心坐标和边长分割缺陷图像。对于所有缺陷图像,最终都要变成50×50或100×100相同的尺寸。
当完成了缺陷图像分割后,需要提取缺陷图像特征参数,以反映该缺陷的基本属性。这里选用图像不变矩作为图像特征参数,其理由是缺陷图像经过二值化已经去除了亮度不一致的区别,只剩下缺陷的几何轮廓信息,而不变矩对图像几何特征具有旋转不变性和尺度不变性,非常适合作为分类的标准。图像的不变矩最后生成7个参数,分别为φ1~φ7,注意在缺陷样本集合中必须将φ1~φ7按列归一化。
3 交叉验证对核函数参数寻优
为进一步提高模型的分类准确率,本文使用了交叉验证的方法[9-10]。在交叉验证中,假设对一类缺陷有N个训练样本,将样本均分为m个分支,1个分支用于训练超球面,剩下m-1个分支验证准确率;然后反过来,将开始用于验证的分支训练超球面,并将开始用于训练的分支验证分类准确率[11],最后求得1-分类的R,a取均值。在基于RBF的SVM中,除样本外,影响分类器的还有罚函数系数C和高斯径向基半径σ参数。为使分类器具有较优准确率,可以将C和σ划分为网格形式进行验证,在实验中取范围为C∈[0.1,0.5,1,5,10,50,100]和σ∈[0.05,0.10,0.15,0.20,…,1],最后得到对应孔洞、划痕和刮擦3类缺陷,参数C=50,σ=0.30;C=50,σ=0.55;C=10,σ=0.70,有较好的效果,通过C和σ解最优化问题,得到SVDD超球面参数,见表1所列。1-分类超球面如图2所示。
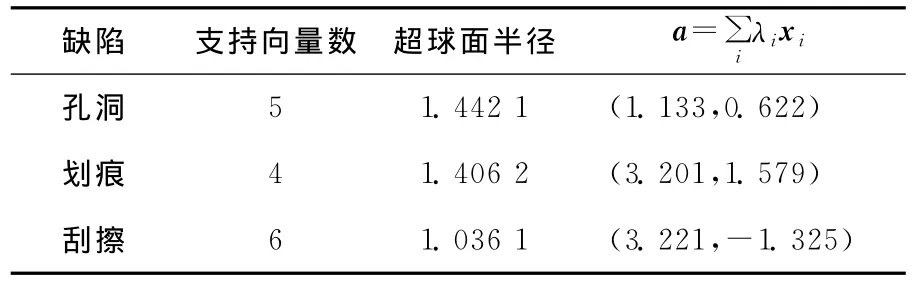
表1 SVDD超球面参数
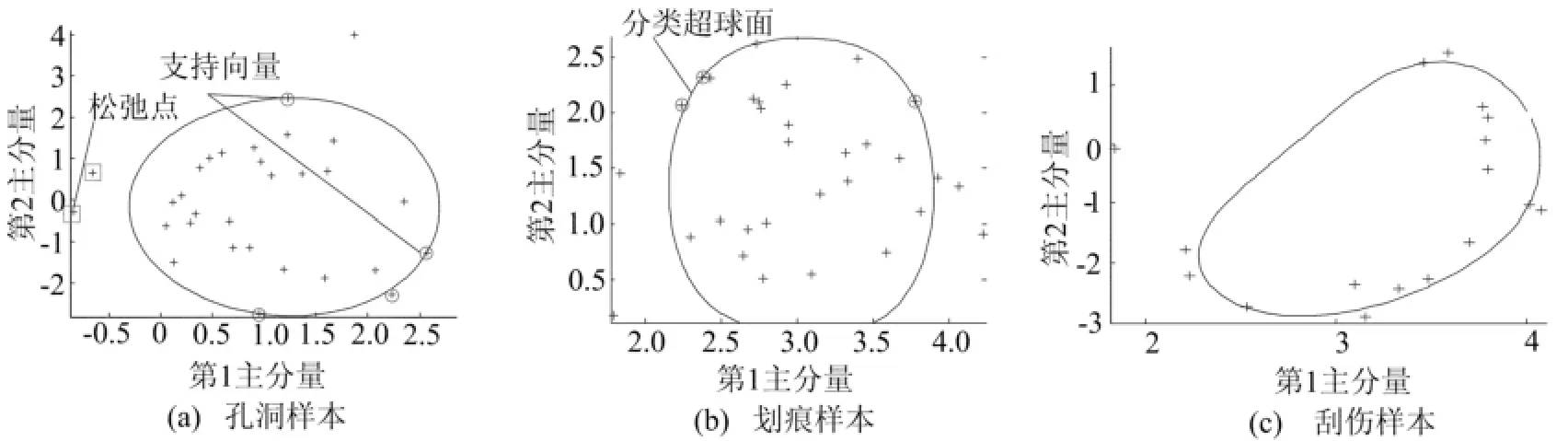
图2 1-分类超球面
4 实验结果及分析
选取2幅图像,并在图像中对孔洞、划痕和刮伤3种缺陷各取20个样本,采用1-分类方法验证,分类结果如图3所示。图3中,标识0表示划痕,1表示孔洞,2表示刮擦。由图3可见,对于划痕缺陷,漏检数目为2、多检的数目为2,误检为孔洞的数目为3;对于孔洞缺陷,漏检数目为2,误检为划痕的数目为2,误检为刮擦的数目为1;对于刮擦缺陷,误检为划痕的数目为2。而将这3种缺陷用Matlab中的svmtrain和svmclassify命令进行分类时,因为要将缺陷先进行两两分类最后合成为多分类,在过程中误差将会扩大,见表2所列。综上所述,使用1-分类方法有效地提高了分类准确率,见表3所列。

图3 缺陷分类结果
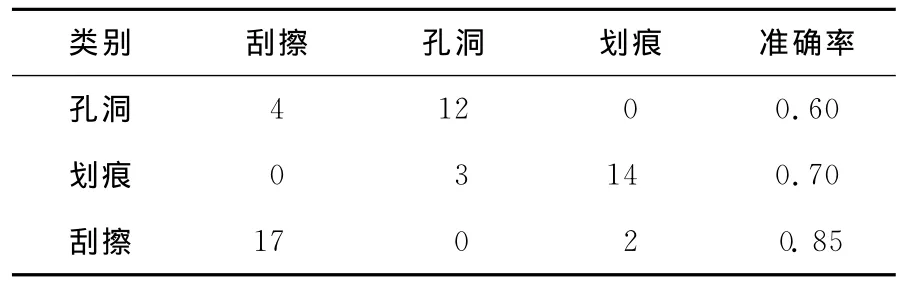
表2 svmclassify两两分类准确率
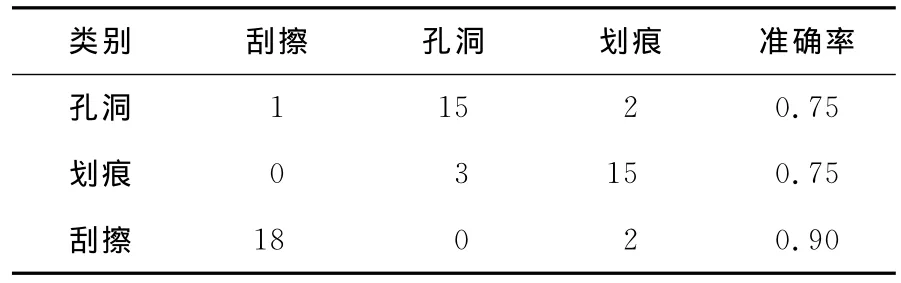
表3 1-分类准确率
5 结束语
分析误分的原因,一方面是实验中的样本准备得还不够充分和有代表性,另一方面是检测时受光照的影响,出现断线和孔洞阴影的情况,使对缺陷区域进行特征提取时受到了影响。此外,由于1-分类方法是固定训练样本的分类方法,因此比启发式学习的分类方法效果差,启发式的分类方法随着测试样本的不断增多而不停地进行样本训练,在一段时间后可以获得更高的准确率,但是其缺点是耗时长、速度慢,相比之下,1-分类方法兼顾了分类准确率和处理速度,适合实时在线检测的应用。
[1]Platt J C.Sequential minimal optimization:a fast algorithm for training support vector machines[J].Advances in Kernel Methods Support Vector Learning,1998,208(4):1-21.
[2]唐 英,李应珍.线性支持向量机多类分类器几何构造方法[J].计算机工程,2012,7(4):152-154.
[3]Scholkopf B,Smola A J.Learning with kernels support vector mahcines,regularization,optimization and beyond[M].MIT Press,2002:187-200.
[4]Ming H Q,Partha N,Yao Yuan.Mercer’s theorem feature maps and smoothing[J].IEEE International Conference on Tools with Artificial Intelligence(COLT),2006,40(5):154-168.
[5]Tax D J,Robert P W.Support vector domain description[J].Pattern Recognition Letters,1999(20):1191-1199.
[6]David M J Tax,Robert P W.Data domain description using support vectors[C]//European Symposium on Artificial Neural Networks,1999:251-256.
[7]Juszczak P,Robert P W.Uncertainty sampling methods for one-class classifiers[J].International Conference on Machine Learning,2003,9(12):42-56.
[8]Tax M J,Alexander Y P,Robert P W.Support vector data description applied to machine vibration analysis[C]//5th Annual Conference of the Advanced Pattern Recognition,1999,353:121-134.
[9]陈 刚,王宏琦,孙 显.基于核函数原型和自适应遗传算法的SVM模型选择方法[J].中国科学院研究生院学报,2012,29(1):62-69.
[10]奉国和.SVM分类核函数及参数选择比较[J].计算机工程与应用2011,47(3):123-128.
[11]王永锋,黄思明,徐 晶.一种通用的基于梯度的SVM核参数选取算法[J].数学的实践与认识,2011,41(1):7-13.

