2种新的单件装配生产过程组合调度规则

李 明， 郭焕银， 曹吉花

（宿州学院 机械与电子工程学院，安徽 宿州 234000）

在单件生产中，调度的困难程度远大于大批量生产方式。单件生产一般具有以下特点［1－3］：产品设计和制造周期长，生产计划和控制有很强的自适应性，设计方案通常根据客户的具体需要而定；产品各部件之间的时序约束关系和成套性要求严格，瓶颈设备的能力和利用率是生产计划与控制的关键环节。因此，以单件小批为主要生产模式的企业，车间的组织与控制方式对其生产调度有着更高的要求［4］，需要采用动态调度策略，其决策规则称为调度规则（dispatching rule）。

以往的研究中提出了很多针对串形工艺路线产品的调度规则［5－8］。仅有少量的调度规则研究的是关于多级装配产品，特别是关于单件装配生产。文献［9］提出了一种工序交付期规则（operation due date rule，简称ODD），该规则在关于产品拖期的各项性能指标中均表现良好。文献［10］提出了2种规则——ECT－FIFO规则和LF－ECT规则，拥有最小的LF（latest finishing time）的工序将获得最高的优先级；结果表明LF－ECT规则表现较好。文献［11］对各种应用在单件生产中的调度规则进行了深入的性能分析，结果表明，最晚完成时间（the latest finish time，简称LFT）规则和改进的最晚开始时间（latest start date，简称LSD）规则表现最好。文献［12］研究了复杂定制产品生产的动态调度，每当一个新的产品生产任务进入系统后，由启发式算法或者是进化算法得到一个新的关于所有工序的调度；然而，这种方法仅仅在毎道加工或装配工序所需的时间是确定性的情况下才是可行的。本文中提出的动态调度规则没有这方面的限制，因为每个调度决定都是根据当时的整个系统的状态得出的。

1 提出的调度规则

本文提出的规则是基于工序的，即调度的产生是基于各装配工序的优先级。下面从3个因素考虑工序的优先级。第1个因素是工序的最晚完成时间（LFT）。如前所述，如果一道工序的实际完成时间晚于它的LFT，那么这道工序所属的产品将必然会拖期，所以LFT是描述一道工序紧急程度的关键因素。这也是一些研究［10－11］发现LFT规则表现很好的原因。第2个因素是这道工序所属路径上的剩余工序数量。如果2道工序拥有相同的或者是很接近的LFT，那么剩余工序数量较多的那道工序显然应该有较高的优先级，因为剩余的工序多意味着有更多潜在的等待时间。第3个因素是这道工序是否在关键路径上。关键路径是一个产品的多个路径中剩余加工时间最长的，所以执行处于关键路径上的工序对推动整个产品的完成有直接的作用。值得注意的是，关键路径并不是静态不变的，随着制造过程的进行，关键路径会发生变化。

下面还有些表示可能会用到：LFTi——工序i的最晚完成时间；RPSi——工序i所在路径上的剩余工序数量；MPT——所有工序的平均加工时间；CPi——一个二进制变量，1表示工序i在关键路径上，0表示工序i不在关键路径上。

很明显，拥有较小的LFT，较大的RPS，等于1的CP的工序将拥有较高的优先级。

1.1 ELFT规则

如果一道工序的完成时间晚于它的LFT，那么这道工序所属的产品必然会拖期。如果完成时间非常接近LFT，意味着这道工序所在路径上的其他工序的松弛时间就会非常短，所以对每一道工序来说，不仅要评定紧急程度，也要考虑在路径上的剩余工序的紧急程度。容易得出如下结论：在关键路径上并且有较小的LFT和较大的RPS的工序应该有较高的紧急程度。工序j的优先级ej可被描述如下：

其中，ω为工序j所在路径上的毎道剩余工序的补偿时间；τ为工序j处于关键路径上的补偿时间。因此ej可以理解为工序j期望的最晚完成时 间（expected latest finishing time，简 称ELFT）。如果工序j剩余的工序比较多，或者处于关键路径上，期望它比实际的LFT更早些完成，那么就给它赋予更高的优先级。明显可以看出ej越小，工序j的优先级越高。

1.2 LFT／RPS／CP规则

对于上文所述的3个因素（LFT、RPS、CP）采用不同的组织形式，可得到LFT／RPS／CP规则。其详细步骤描述如下：

（1）如果一台机器处于空闲状态，而且有候选工序等待在这台机器上执行（不考虑等待工序），将这些候选工序按照LFT的升序排列。

（2）考虑已经在步骤（1）中排好序的工序，对任意工序i满足i≥1和LFTi＜LFT1＋MPT，这部分工序的集合命名为A。然后以相同的1／3的概率执行步骤（3）、（4）或（5）去调整A 中工序的排列顺序。

（3）保持A中工序的排序不变，并转到步骤（6）。

（4）将A中的工序按照RPS的降序重新排列并转到步骤（6）。

（5）按照CP的值将A分为2个子集，第1个子集包含A中CP为1的工序，第2个子集包含A中CP为0的子集。然后分别将2个子集的工序按照LFT的升序重新排列，转到步骤（6）。

（6）选择A中排在第1位的工序并执行。

2 数值仿真实验

在Visual Studio 2003环境下开发了单件装配生产过程仿真程序，考虑如下单件装配生产车间：有20个工作站，每个工作站有1台机器。每个产品包含20个装配工序，分别在这20台机器上执行。工序执行时间服从［10，30］的均匀分布。产品随机到达，到达间隔时间服从参数为23个时间单位的负指数分布。数值试验表明在这个参数下，在制品水平可达到稳定状态并且各机器的负载水平较高。新到产品的交付期由关键路径长度（li）、宽容系数（c）和产品到达时间（ai）决定，即产品i的交付期di＝ai＋cli。试验中取c＝2。试验中将生产500个产品，除去铺线的50个和收线的50个，统计中间400个产品的拖期产品数和总拖期时间，作为评判调度规则效率的标准。

2.1 ELFT规则中参数的影响

在ELFT规则中有ω和τ2个参数。

当ω＝0，τ＝0时，ELFT规则也就是LFT规则，拖期产品数为88个，总拖期时间为2161个时间单位。调整这2个参数的值，在不同参数的ELFT规则下对同一组产品进行生产过程仿真，得到如图1所示的试验结果。

图1 不同参数下的拖期产品数与总拖期时间

从图1中可以看出，在ω∈［0，3］和τ∈［0，27］时，ELFT规则要优于LFT规则。其中在区间ω∈［0，3］，τ∈［12，24］表现最为优越。但是，当ω＞4时，此规则的效率就开始降低，甚至比LFT规则还要差。根据仿真实验，τ的值可选为工序的平均时间，而ω的值可选为工序的平均时间／工序数。

2.2 提出规则与其他规则的比较

下面将本文提出的动态调度规则的效率，与其他装配生产动态调度研究中表现较好的规则进行比较。由于文献［10］提出的ODD（operation due date）规则实际上只是LSD（the latest starting date）规则的一种，而文献［12］中提出的refined－LSD是一个“try－every－rule”方法，即要尝试规则的参数取值，经比较再选取最好的那个，这个方法现实意义不大而且结果和LSD规则相比也几乎相同，所以选取文献［10－12］的其他几个规则来比较，包括LFT（the latest finishing time）规则、EDD（the earliest due date）规则、LSD 规则、ECT（the earliest completing time）规则。其中EDD和ECT都是基于产品的调度规则，即产品每道工序的优先级都是根据产品的某个性质来决定的，比如根据产品的交付期；其他几个，包括本文提出的2个都是基于工序的调度规则。取10组产品分别用这几种规则进行调度，比较拖期产品数和总拖期时间，试验结果见表1和表2所列。表中L／R／C规则表示LFT／RPS／CP规则。

表1 各规则下拖期产品数比较

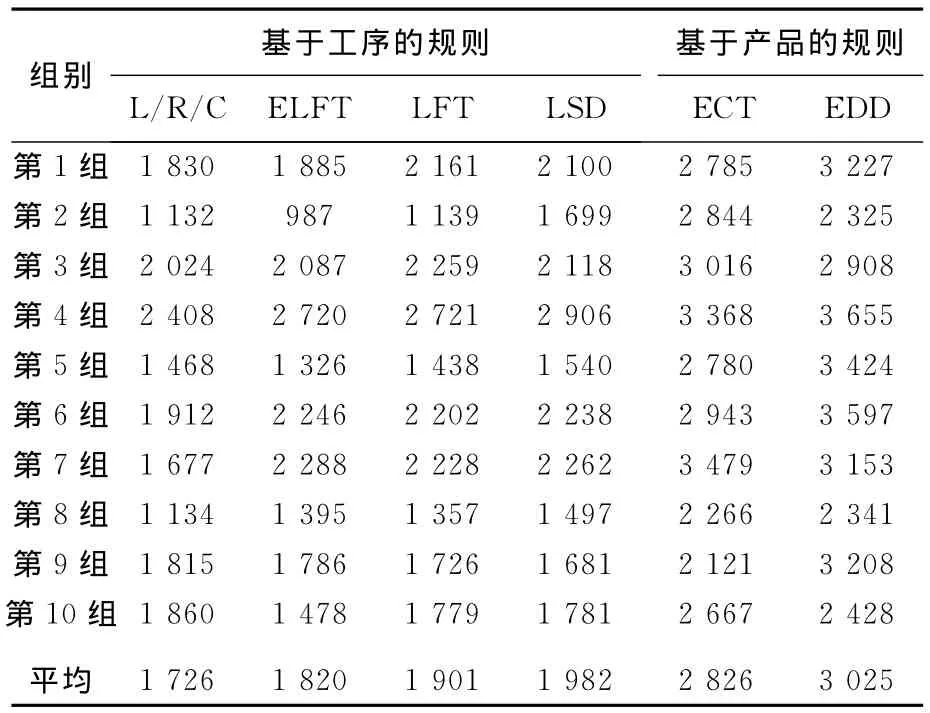
表2 各种规则下总拖期时间比较

从表1和表2可以看出，在单件装配生产的动态调度过程中，在减少拖期产品数和减少总拖期时间方面，基于工序的调度规则要明显地优于基于产品的调度规则（ECT、EDD）。

此外，所提出的2种规则与另外2种基于工序的动态调度规则（LSD、LFT）相比，能更加有效地减少产品的拖期情况。2种LFT＋RPS＋CP规则调度下拖期产品数分别比LFT规则少6.3%和3.0%，分别比 LSD 规则少10.3%和7.1%；在减少总拖期时间方面也表现较好：LFT／RPS／CP规则和ELFT规则总拖期时间比使用LFT规则时分别少了9.2%和4.3%，比使用LSD规则时分别少了12.9%和8.2%。由此可见所提出的这2种动态调度规则能更有效地减少单件装配生产过程中的拖期产品数和总拖期时间。

3 结束语

本文研究了在单件装配生产环境中的动态调度问题，每个产品都有自己独特的树形工艺路线、工序时间、交付期，而且随机到达且符合负指数分布。本文提出了2种可用于上述情况的动态调度规则：ELFT规则和LFT／RPS／CP规则。为了检验这些新规则的性能表现，开发了单件装配生产仿真软件并做了大量的数值仿真试验。试验结果表明：ELFT规则的参数取值对规则效率的影响很大，可以根据仿真试验的结果经验性地将τ的值选为工序的平均时间，而ω的值可选为工序的平均时间／工序数；基于工序的调度规则表现远远优于基于产品的调度规则；所提出的2种规则与LSD规则和LFT规则相比，能更加有效地减少产品的拖期情况。

［1］Tu Y L.Real－time scheduling and control of one－of－a－kind production［J］.Production Planning ＆ Control，1997，8（7）：701－710.

［2］Kuhlmann T H.A revolving planning and control system［C］／／Proceedings of New Approaches Towards One－of－akind Production，Bremen，Germany，1991：95－112.

［3］Hirsch B E，Kuhlmann T H.Harmonization of decentralized，autonomous production areas［C］／／Proceedings of IFAS CIM in Process and Manufacturing Industries，Espoo，Finland，1992：69－74.

［4］牛兴华.一种独立制造岛作业计划的编制方法［J］.天津理工学院学报，1999，15（2）：18－23.

［5］Chiang T C，Fu L C.Using dispatching rules for job shop scheduling with due date－based objectives［C］／／Proceedings of the 2006IEEE International Conference on Robotics and Automation，Orlando，Florida，2006：1426－1431.

［6］Dominic P D D，Kaliyamoorthy S，Kumar M S.Efficient dispatching rules for dynamic job shop scheduling［J］.International Journal of Advanced Manufacturing Technology，2004，24（1／2）：70－75.

［7］Chiang T C，Fu L C.Solving the FMS scheduling problem by critical ratio－based heuristics and the genetic algorithm［C］／／Proceeding of the 2004IEEE Conference on Robotics and Automation，Vol 3，New Orleans，LA，USA，April 26－May 1，2004：3131－3136.

［8］王海瑶，蒋增强，葛茂根.基于规则组合的Job Shop多目标柔性调度方法 ［J］.合肥工业大学学报：自然科学版，2010，33（1）：14－18.

［9］Reeja M K，Rajendran C.Dispatching rules for scheduling in assembly jobshops，part 1［J］.International Journal of Production Research，2000，38（9）：2051－2066.

［10］Mohanasundaram K M，Natarajan K，Viswanathkumar G，et al.Scheduling rules for dynamic shops that manufacture multi－level jobs ［J］.Computers and Industrial Engineering，2002，44（1）：119－131.

［11］Choi B K，You N K.Dispatching rules for dynamic scheduling of one－of－a－kind production［J］.International Journal of Computer Integrated Manufacturing，2006，19（4）：383－392.

［12］Hicks C，Song D P，Earl C F.Product due date assignment for complex assemblies［J］.International Journal of Production Economics，2002，76（3）：243－256.