VIVS准混沌算法的初值敏感性检验方法

龙德浩,陈志清

(1.四川大学,成都 610064;2.成都大学,成都 610106)

1 引 言

1963年,Lorenz在研究天气预报方程时发现了混沌现象。随后,混沌算法以其独特的初值敏感性深深地吸引着一代又一代学者,直到今天。因为初值敏感性涉及的面较宽,涵盖自然、政治、经济等学科领域。就抗干扰而言,初值敏感性强意味着能同时提高定位系统的速度分辩能力和距离分辩能力;能有效抑制扩频通信的地址干扰和人为相关干扰;对信息安全而言,是反“相关分析”、反密码丢失的根本方法;对弱信号接收,例如无线探矿、深空通信等,是一条全新的数字编码思路。因此,人们希望找到一种新的编码方法,它既具有经典混沌算法独特的初值敏感性,又能克服经典混沌算法难以克服的“同步难”问题。到如今,混沌理论经历了上世纪70年代的“机理”、80年代的“建模”、90年代及其随后的“应用”研究,已逐步迈向应用,特别是变初值变结构(VIVS)准混沌算法[1-4]克服了经典混沌算法的“同步难”问题。至于初值敏感性,不同领域、不同学者,其理解是不尽相同的。催化化学家把它理解为“催化剂”,只需添加极少量的“催化剂”,即可使化学反应的速率提高百倍、千倍、万倍……就通信而言,我们把它理解为:任意邻近的初值产生的0/1混沌序列都是彼此无关的,进而是统计独立的。然而,在用数学语言表达此定义时,却遇到了互相关函数绝对极大值的“统计分布难”问题。尽管极值分布理论在上世纪60年代早有定论,但由经典的3种分布类型[5]所导出的结果,偏离物理概念较远。不得已我们拟议了“双序列平面图解法”,这种方法简单、直观,但只能定性[6]。定性检验结果表明,VIVS编码算法具有初值敏感性,故简记为VIVS准混沌算法。如何定量地检验编码(含混沌)算法的初值敏感性呢?工程应用专家很关心这个问题。然而,近半世纪过去了,至今仍未解决。笔者近两年基于Г л й в е н к о极限定理[7],再次探讨了通用编码算法的初值敏感性检验方法,旨在抛砖引玉。

2 通用编码算法的初值敏感性检验方法

2.1 初值敏感性检验方法的定义

我们拟议的初值敏感性检验方法的定义包含5个步骤。

(1)首先,给定任意邻近初值矩阵

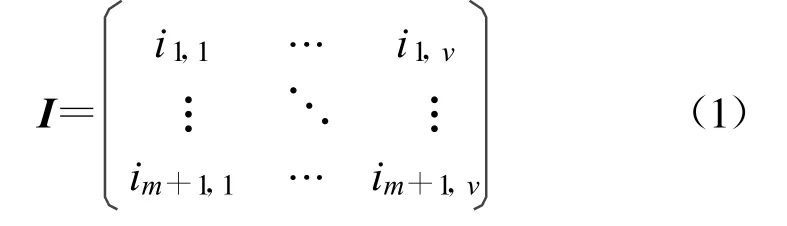
共计m+1行,v列。其中,ii,j(i=1,2,…,m+1;j=1,2,…,v)的取值决定于被检编码算法所采用的数制。但无论哪种数制,任意相邻两行的数值都必须尽量接近,例如,彼此相邻1 bit。而后把这组初值I逐行代入待检编码算法,从而生成待检数据矩阵

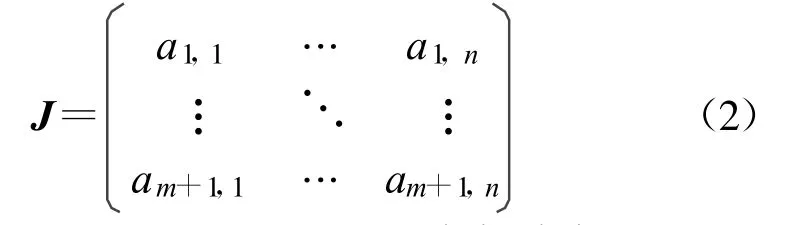
共计 m+1行,n 列。其中,ai,j=′0′或′1′;i=1,2,…,m+1;j=1,2,…,n。n=2 000～3 000,不宜太长,因为初值敏感性总是发生在启动编码算法的初始阶段;但也不能太短,否则无法检验到某些算法存在的初值敏感性的过渡过程。m=2 000～8 000,旨在使所求的经验分布更接近于母体的理想概率分布。

(2)求出矩阵J中任意一行,例如第i行的自相关函数,而后除以序列的长度n,即得归一化自相关函数矢量b11。

(3)依次求出矩阵J中相邻两行的互相关函数

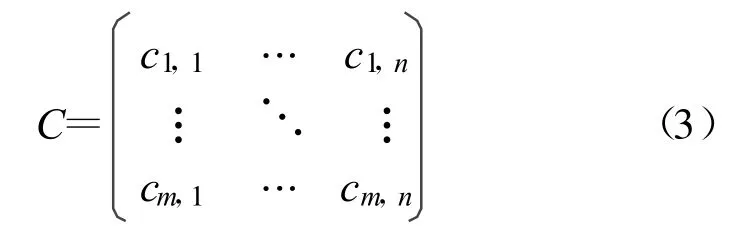
共计m行,n列。

(4)将C以“同一 n”标准化之,即得标准化互相关函数矩阵

而后取绝对值,再取极大值,即得R的绝对极大值矢量

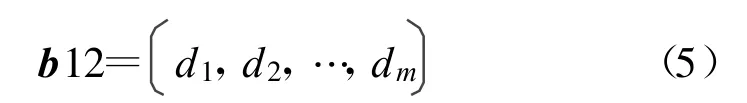
并称之为待检编码算法的“初值敏感性检验样本”,记为 b12。这样,一切可能 b12的总体,就是初值敏感性检验的样本空间 Ψ;当I给定时,b12即为总体Ψ的一组观测值。因为b12是一个绝对极大值向量,故本文提出的初值敏感性检验方法实质上属于极大值检验范畴。鉴于此,初值敏感性检验的首要任务就是求“b12不大于预先给定的门限值th”这一事件的概率。为此,必须先求出总体 Ψ的概率分布。

(5)由 Г л й в е н к о极限定理得知 :当 m 很大时 ,总体 Ψ观测值b12的经验分布,就是母体 Ψ的良好的近似概率分布。这样,有了母体 Ψ的概率分布,即可求出上述“事件”的概率及其相关参数。

2.2 初值敏感性检验步骤

这个“检验步骤”实质上是编写“通用编码算法初值敏感性检验程序”的流程图。

第一,依照2.1节,求初值敏感性检验的观测值矢量 b12;第二,求 b12的升序结构;第三,求初值敏感性检验样本空间 Ψ的概率分布;第四,求b12不大于门限值th的概率;第五,求 b12大于门限值 th的概率;第六,求门限值 th在b12升序结构中的位置;第七,求 b12中任意一点,例如极大值、中位置等的概率;第八,求 b12的极大值;第九,求 b12的样本平均值;第十,求 b12的统计平均值;第十一,求b12的样本标准差;第十二,求b12的统计标准差。

2.3 初值敏感性检验的判决准则

设门限值 th=0.1000∈b12。如果观测值 b12不大于门限值th的概率为

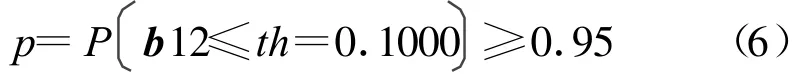
或 其“补”概率为

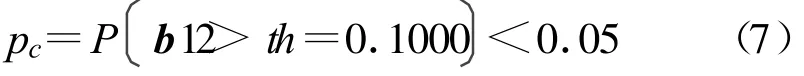
则产生此被检序列的编码算法具有初值敏感性;反之亦然。

3 通用编码算法初值敏感性检验文件

按照第2.2节的“检验步骤”,逐一写出“通用编码算法初值敏感性检验”文件

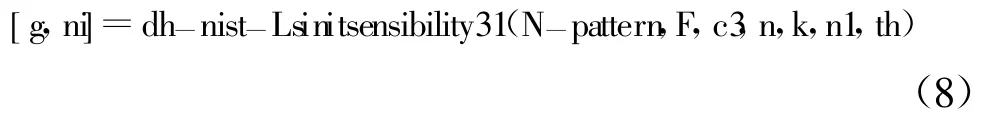
的参数:主文件名:dh-nist-Lsinitsensibility31,计算机语言:matlab;输入矩阵的行数:N-pattern,2 000～8 000;调用子函数的符号:F,matlab语言调用自编功能函数的符号;输入数据文件名:c3.mat,一切符合式(1)和式(2)要求的matlab(0,1)数据文件;输入矩阵的列数:n,2 000～3 000;最大相关时间:k,k=n,2 000～3 000;任意指定的数值:n1,n1∈b12,检验者感兴趣的数值,例如中位数、极大值、极小值等;初值敏感性门限值:th∈b12,随工程要求而定,本例th=0.1000;反馈矢量和频率:[g,ni],ni为所求的b12的密度函数,g为所求的功能参数矢量。

4 VIVS准混沌算法初值敏感性检验

(1)调用初值敏感性检验通用文件

(2)VIVS-c6001.b12样本观测值的数据结构

被检母体 Ψ的本次观测值VIVS-c6001.b12的数据结构(参见2.2节的检验步骤)为

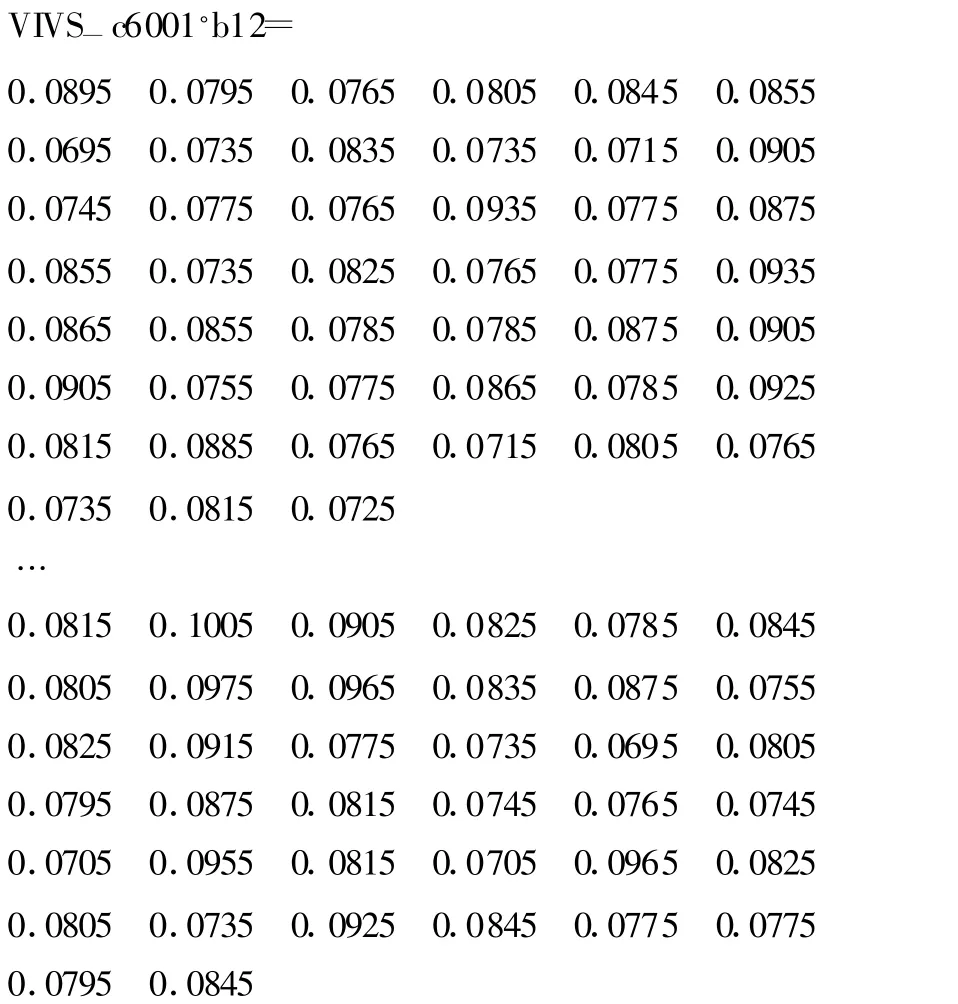
其图像如图1所示。

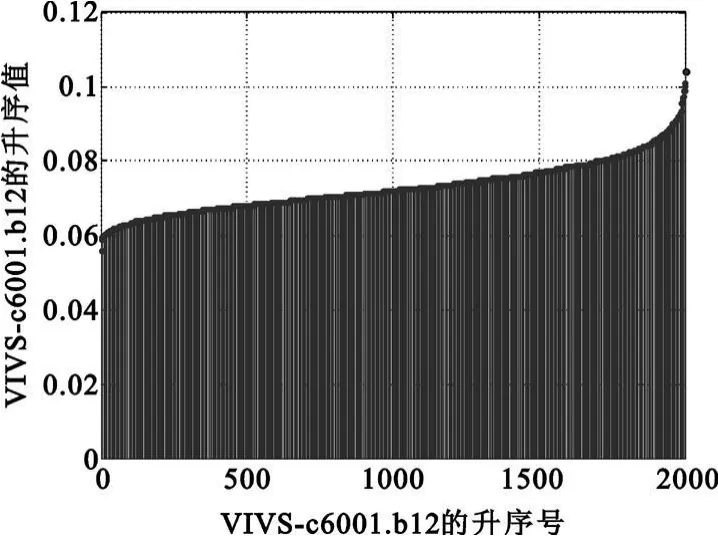
图1 彼此相邻1 bit的VIVS-c6001.b12的升序图Fig.1 Sorting chart of VIVS-c6001.b12 adjacent to each other 1 bit

由图1可知,VIVS准混沌算法的互相关函数的绝对极大值共计2 000个,最大值劣于0.12,即互相关系数较小。

(3)VIVS-c6001.b12母体 Ψ的概率密度函数(数字式)及其参数[g,ni]

母体 Ψ的观测值VIVS-c6001.b12的经验分布函数(见2.2节的检验步骤)为

其图像如图2所示。

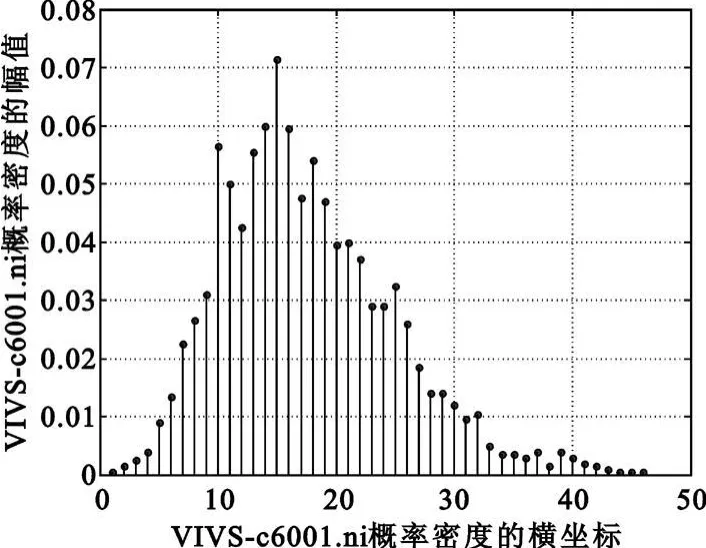
图2 彼此相邻1 bit的VIVS-c6001.ni概率密度Fig.2 Probability density of VIVS-c6001.ni adjacent to each other 1 bit

由 Г л й в е н к о极限定理得知 ,因为观测值 VIVS-c6001.b12的数据量较大,等于2 000,故其经验分布VIVS-c6001.ni是总体 Ψ的概率密度的一个良好近似。由此,即可求出与VIVS准混沌算法有关的几个主要参数,如表1所示(见2.2节的检验步骤)。

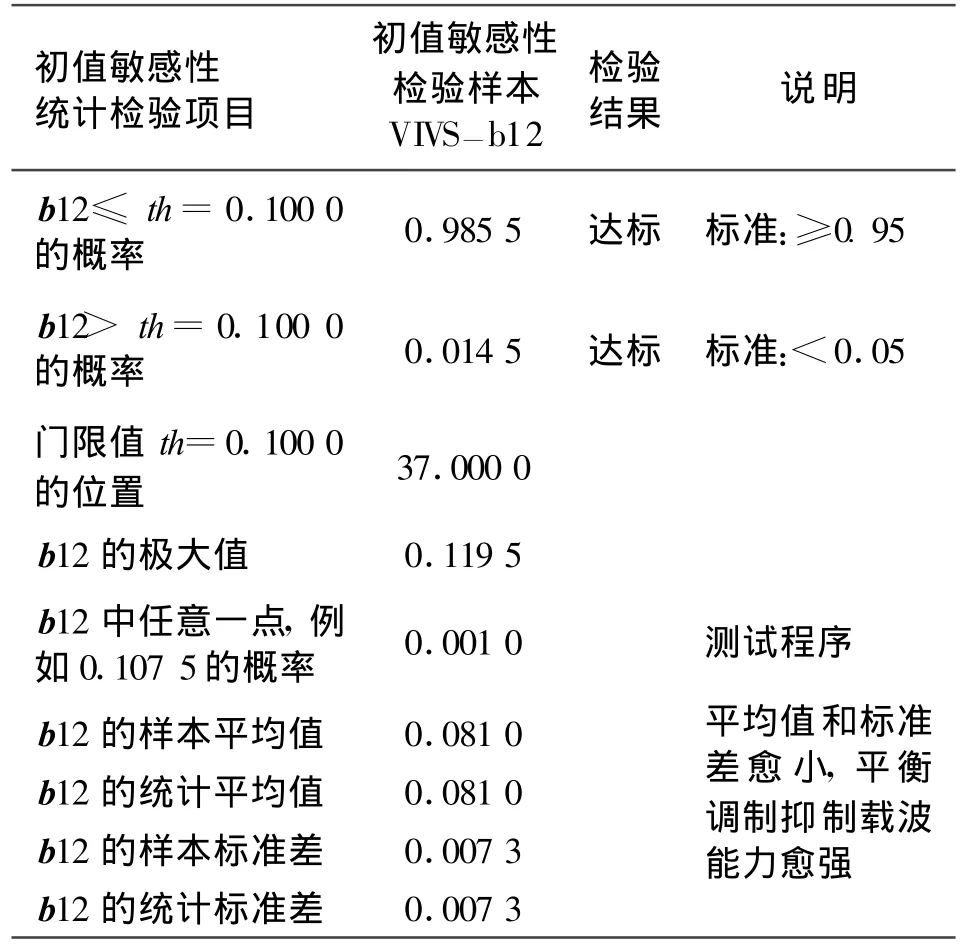
表1 VIVS准混沌算法初值敏感性检验主要结果Table 1 Sensitivity of the initial value with VIVS quasi-chaos algorithm

(4)初值敏感性样本值VIVS-c6001.b12不大于门限值th=0.100 0的概率是

5 结 论

由式(8)得知,对于任意给定的彼此相邻1 bit的初值矩阵I产生的样本VIVS-c6001.b12不大于给定门限电平 th=0.100 0的概率为0.985 5,大于0.95,故依据判决准则式(6),被检验的VIVS准混沌算法以概率0.985 5具有初值敏感性,从而为证明VIVS准混沌算法满足Shannon完全保密性定理的充要条件和探索大容量CDMA码族奠定了理论基础,节省了大量的计算时间。

[1]陈志清,龙德浩.复合迭代算法及其应用[J].四川大学学报(自然科学版),1997,34(5):621-628.CHEN Zhi-qing,L ONG De-hao.Composite iterative algorithm andits application[J].Journal of Sichuan University(Natural Science Edition),1997,34(5):621-628.(in Chinese)

[2]陈志清,龙德浩.二重变初值流密码算法[J].四川大学学报(自然科学版),1997,34(6):791-800.CHEN Zhi-qing,LONG De-hao.Double Varying Initial Values Stream Cipher Algorithms[J].Journal of Sichuan University(Natural Science Edition),1997,34(6):791-800.(in Chinese)

[3]陈志清,龙德浩.变初值变结构准混沌:密码学发展的新方向[J].大自然探索,1997,16(4):46-49.CHEN Zhi-qing,LONG De-hao.Varying Initial Conditions/Varying Structure Quasi-Chaotic Cipher Streams:A New Direction in Cryptography[J].Discovery of Nature,1997,16(4):46-49.(in Chinese)

[4]陈志清,龙德浩.变初值/变结构准混沌滚动密钥发生器[J].电讯技术,1997,37(6):48-52.CHEN Zhi-qing,LONG De-hao.Change the initial value/variable structure quasi-chaos scroll key generator[J].Telecommunications Engineering,1997,37(6):48-52.(in Chinese)

[5]陈希孺.数理统计引论[M].北京:科学出版社,1981:534.CHEN Xi-ru.Mathematical Statistics Introduction[M].Beijing:Science Press,1981:534.(in Chinese)

[6]陈志清,龙德浩.变结构密码算法[J].四川大学学报(自然科学版),1998,35(2):210-217.CHEN Zhi-qing,LONG De-hao.Variable structure cryptographic algorithms[J].Journal of Sichuan University(Natural Science),1998,35(2):210-217.(in Chinese)

[7]茆诗松,程依明,濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社,1983:229.MAO Shi-song,CHENG Yi-ming,PU Xiao-long.Probability and Statistics tutorial[M].Beijing:Higher Education Press,1983:229.(in Chinese)

[8]龙德浩.编码识别汽车防撞雷达[J].电讯技术,2009,49(7):41-46.LONG De-hao.Encoding recognition automotive collision avoidance radar[J].Telecommunications Engineering,2009,49(7):41-46.(in Chinese)