回油型面结构对计量装置特性影响研究

曾德堂 ，赵威力 ，王 曦 ，徐 敏

（1.北京航空航天大学能源与动力工程学院，北京 100191；2.西安航空动力控制有限公司，西安 710077）

0 引言

回油型面结构体现计量装置燃油流通能力，并对计量装置的稳态性和计量特性有着重要影响。因而，对其回油型面结构机理进行深入研究，设计合理的回油型面结构对提高燃油计量装置稳定性和计量特性具有重要意义。目前，中国在设计上基本采用预估与试验相结合的办法，但该方法存在设计周期长和成本高等不足，制约着回油型面结构对计量装置特性影响机理进行深入研究。现今中国对具体回油型面结构设计及特性分析研究资料较少。刘正等人对某型压差计量装置结构设计和性能进行计算研究[1]；文元江用EASY5分析回油式压差活门特性[2]；文献[3]探索研究了回油型面结构与流量、压力增益及流量-压力系数等的关系。

本文以某型燃油计量装置回油型面为研究对象，通过仿真得到不同回油型面结构计量装置稳定性及计量特性，并对特性影响机理进行了深入分析。

1 计量装置和回油型面结构

1.1 计量装置

某型燃油计量装置结构与回油型面位置如图1所示。该装置主要由壳体、压差和计量活门组成，其回油型面集于压差活门中。压差活门通过调节回油型面开度，使装置左右压差恒定，从而使计量流量与流通面积成线性关系，当计量装置预调好后，其压差活门回油型面结构处于临界开启位置，而此时计量活门开口位置距临界开启位置为1.3 mm。

1.2 回油型面结构

回油型面面积见表1。其结构主要有三角形、矩形、圆形，如图2所示。

表1 回油型面面积

2 数学方程及仿真模型

2.1 数学方程

根据压差活门结构及牛顿运动定律，其运动方程为

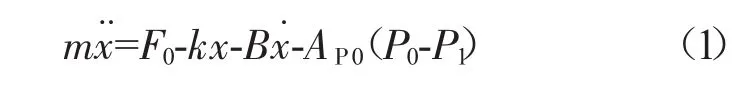
由容积变化引起压力变化方程[4]得

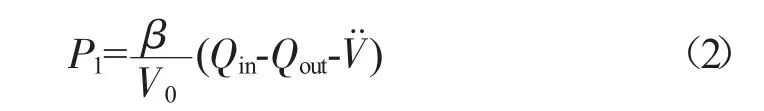
式中：β为燃油弹性模量；Qin为流入P1腔流量；Qout为流出P1腔流量；V0为P1腔初始体积。

P1腔体积变化为

式中：V为P1腔体积；V0为P1腔初始体积；AP0为受力面积；x为位移。

由流量公式可知，流入P1腔流量为

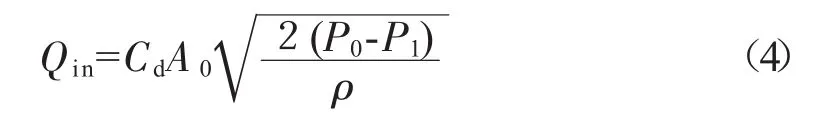
式中：Cd为流量系数；A0为计量活门面积；ρ为密度。

同样，由流量公式可得流出P1腔流量为

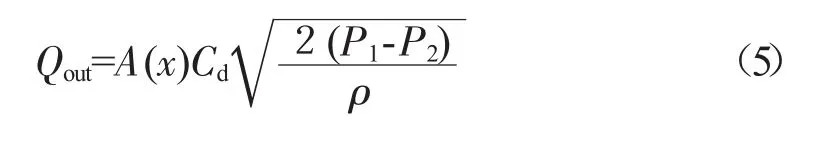
式中：A(x)为面积；P2为发动机喷嘴前压力。

2.2 仿真模型

根据燃油计量装置工作原理[4-5]、回油型面特点及式（1）～（5）建立燃油计量装置数学仿真模型，如图3所示。模型主要包括压差活门、计量活门、P1腔、回油型面、输入量和输出量等模块，且与燃油计量装置结构（图1）相对应，其模块支持回油型面结构仿真计算,模型参数见表2。在仿真计算时，计量活门位移作为输入信号，而压差活门开度面积和流量作为输出量。

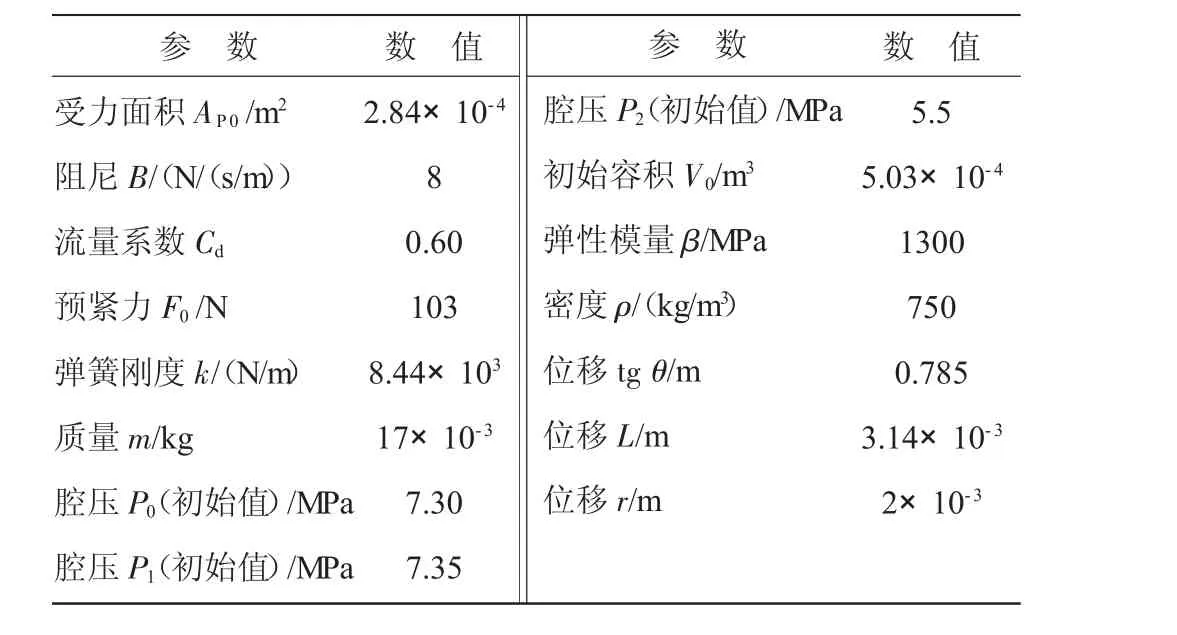
表2 计量装置结构参数和初始值

2.3 回油型面面积

为了对比输入相同燃油量时各回油型面结构对装置特性的影响，仿真时假定回油型面结构的最大面积和最大位移量相同，压差活门位移量与三角形、矩形及圆形回油型面开度面积关系如图4所示。

图4 回油型面面积与位移关系

2.4 输入信号

在验证回油型面结构对装置特性的影响时，采用的仿真输入信号（即计量活门位移量）如图5所示。当仿真时间 t=0～0.5 s时，输入信号为 0；当 t=0.5～2.5 s时，输入信号以5 mm/s斜率增长，其中，当t=0.76 s时，输入信号为1.3 mm，此时装置计量活门打开；当t=2.5～3.0 s时，装置的计量活门位移达到最大值10 mm。

图5 装置仿真输入信号

3 结果及分析

评价计量装置性能标准主要是计量精度和装置稳定性等，而上述标准则是通过压差活门的回油型面开度面积和计量流量来体现，仿真时给仿真模型输入如图5所示的信号，输出量为各回油型面开度面积和计量流量。

各回油型面结构开度面积和计量流量仿真结果如图6～11所示。

从图6中可见，当t=0～3 s时，三角形回油型面开度面积仿真结果与输入信号趋势基本一致，即回油型面开度面积与输入信号同步稳定增大，即使当输入位移量为1.3 mm时（装置处于临界开启状态），回油型面开度面积仍无震荡现象。

从图7中可见，三角形回油型面流量仿真特性的变化趋势与如图6所示的其开度面积的基本一致，计量流量与输入信号同步稳定增长。

图6、7的仿真结果说明，在图5输入条件下，三角形回油型面计量装置具有良好的稳定计量特性。

从图8中可见，当t=0～0.5 s时（即输入信号为0），仿真结果出现轻微震荡现象；随着仿真时间的增加，当t=0.5～1 s时，仿真结果震荡加剧，而此时间段包含输入位移量为1.3 mm时临界开启位置，这也充分说明矩形回油型面结构在临界开启点附近稳定性变得更差。当t=1～3 s时，随着仿真时间的增加，输入信号远离开启点，装置稳定性又逐渐变好，与输入信号趋势基本保持一致。

图6 三角形回油型面开度面积

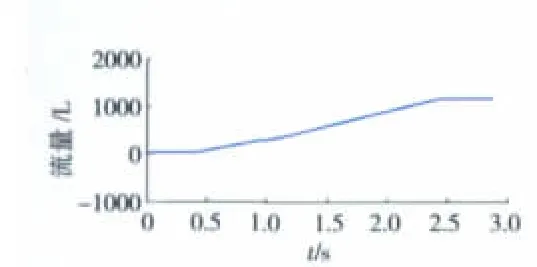
图7 三角形回油型面流量仿真特性

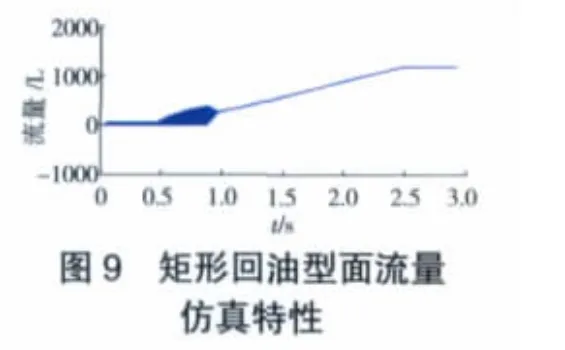
从图9中可见，矩形回油型面流量仿真特性的变化趋势与如图8所示的其开度面积的基本一致，仅在非稳定区域震荡幅度相对小些。

图8、9的仿真结果说明，在图5输入条件下，矩形回油型面在临界开启点前，装置的计量特性都变差，特别是装置处于临界开启点附近震荡加剧。

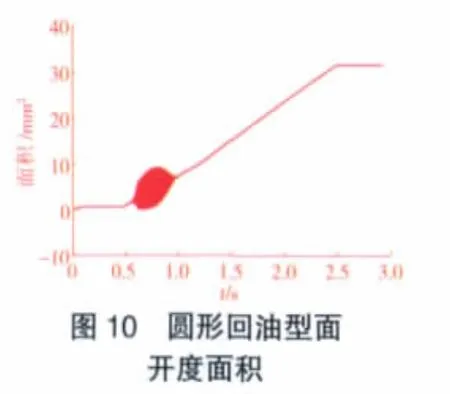
从图10中可见，当t=0～0.5 s时，即输入信号为0时，圆形回油型面仿真结果稳定，装置未开启；随着仿真时间的增加，输入信号接近临界开启点附近（即t=0.5～1.0 s时），仿真结果出现震荡现象，这充分说明了圆形回油型面结构在临界开启点附近稳定性变差；随着仿真时间的增加，输入信号远离临界点，装置稳定性变好，且与输入信号趋势保持一致。

从图11中可见，圆形回油型面流量仿真特性的变化趋势与如图10所示的其开度面积基本一致，仅在临界点附近震荡幅度相对小些。

图10、11的仿真结果说明，在图5输入条件下，圆形回油型面在临界位置点附近，装置计量特性变差，但随着输入信号增大或减小，输入信号远离临界点，装置特性都变好。

4 结论

（1）以Matlab为平台建立的燃油计量装置仿真模型，即节省了设计成本，又缩短了研制周期。（2）仿真结果表明，在相同条件下，三角形回油型面结构性能优于圆形回油型面结构的，而矩形回油型面结构的计量特性和稳定区域均比三角形和圆形回油型面结构的差。同时，在临界开启点，矩形和圆形回油型面结构计量流量出现震荡现象，而三角形回油型面结构计量流量则是稳定的。

本文的研究和分析结果可为科研设计人员快速设计和选择合理回油型面结构提供参考依据。

[1]刘正，郭迎清.某型压差计量装置结构设计及性能计算[C]//中国航空学会第十二届发动机自动控制学术会议论文集.株洲：中航工业动力机械研究所，2004：158-162.

[2]文元江.用EASY5分析式压差活门特性 [J].机床与液压，2005（1）：21-26.

[3]曾德堂，王曦.燃油计量装置回油型面特性分析[J].航空发动机，2010，36（6）：22-25.

[4]孙健国.现代航空动力装置控制[M].北京：航空工业出版社，2001：58-102.

[5]ZENG De-tang，WANG Xi.Design and analysis of damping hole for a fuel metering valve[C]//The 2010 International Conference on Mechanicaland ElectricalTechnology,IEEE-2010：622-626.

[6]Maiti R,Pan S,Bera D.Analysis of a load sensing hydraulic flow control valve[C]//Proc.of 3rd JHPS International Symposium on Fluid Power,Yokohama,Japan:307-312.

[7]Wu D,Rurton G,Schoenau G,et al.Analysis of a pressure compensated flow control valve[J].ASME Journal of Dynamic Systems,Measurement,and Control,2007，129（2）：203-211.

[8]Katsuya S，Ikuo N b.Thoma pressure regulator valve by Bondgraph[J].Simulation Practice and Theory,1999（7）：