细分方法中对显著扭曲面片的校正处理①

孙 林

(合肥工业大学数学学院，安徽 合肥 23009)

0 引言

细分方法是根据初始控制顶点，经过连续细化而生成曲线曲面的离散化造型方法，其起源可以追溯到1956年de Rham的割角逼近方法.在1974年Chaikin提出的曲线生成方法引起CAGD领域的关注.1978 年 Catmull和 Clark[1]，Doo 和 Samin[2]则分别提出了任意拓扑网格上的双三次和双二次B样条曲面细分方法，使得细分方法开始应用于曲面造型.1987年Loop[3]提出了一种基于三角形网格的细分方法，将四次三项Box样条推广到任意的三角形网格上.1991年Dyn[4]给出了一种可达C2连续的四点逼近格式.1998年 Sederberg[5]等提出了广义Doo－Sabin细分规则和广义Catmull－Clark细分规则，使得NURBS成为它的子集.其中，若细分方法生成的极限曲面通过全部原控制顶点，则称为插值细分方法，否则称为逼近细分方法.上面提到的Doo－Sabin细分、Catmull－Clark细分、Loop细分等是逼近方法;而Kobbelt[6]方法和蝴蝶方法等是插值方法.

细分方法具有拓扑任意性这一重要优点，可以有效解决曲线曲面的造型问题.其中Doo－Sabin方法可以很好的保持网格一些转角特征.实际应用中，发现上述几种基本细分方法在相对正规性的网格上得到很好的结果，但当网格中出现显著扭曲面片时，就会出现不理想的细分结果.针对这种情况，文献[7]给出了基于泊松网格编辑方法控制网格变形，在Loop和Catmull－Clark两种细分模式下有良好的结果，但其实施过程需要手工指定目标网格区域，不便于细分过程的自动化.

本文提出一种比较通用的基于相邻点的面片扭曲变形控制方法，可以根据需要集成到经典Doo－Sabin方法，Catmull－Clark方法和 Loop方法中，实现细分方法对扭曲面片的校正优化处理.

1 经典细分方法在处理扭曲面片时的不足

经典细分方法在处理规则网格时，能给出具有光滑性和连续性等良好的结果;但在处理的含有显著扭曲面片时，出现的结果就不是很理想，以汽车或船舶造型中用网格模拟钢板扭曲为例，由于材料的韧性，会产生均匀向性扭曲，如图1中原始网格上，面片EFGH绕面片的一个中心轴转动120°，带动面片CDEH产生显著扭曲.理想状态下，原始网格均匀扭曲得到的新网格，是一个可展曲面，这个曲面在一个平面上重新展开时，期望它能得到与原网格几何特性相同的结果.对于图1中的扭曲网格，理想细分结果应该是中间部分保持宽度的情况下均匀变化接合首尾面片，如图1中理想扭曲细分所示，这个网格平展后基本保持与原始网格一致.经典细分方法在处理规则网格时都能达到一些光滑性较好的结果，但没有顾及到上述这种显著扭曲的情形，在含有显著扭曲面片的场合下得到的结果往往与期望结果有出入，如图2所示，两种经典细分方法对图1中有扭曲面片的网格进行细分后的结果及其在平面上展开的结果.

可以看到，两种细分结果的光顺性都非常好，这个是它们的优点;但在扭曲角度较大的情况下，经典细分方法得到的网格在平面展开后，中间收缩得非常接近，以致几乎丧失了原来面片的基本特征，这种扭曲能模拟类似橡胶材质等弹性面的扭曲变形，与钢板等韧性材料均匀受力扭曲变形的实际情况相差甚远.因而对这种模拟韧性材质显著扭曲面片情况下的网格进行有针对性的处理是非常必要的.

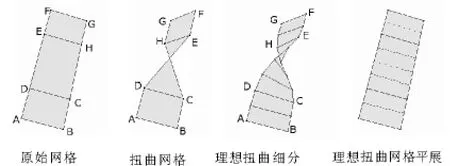
图1 含扭曲面片的网格理想变形

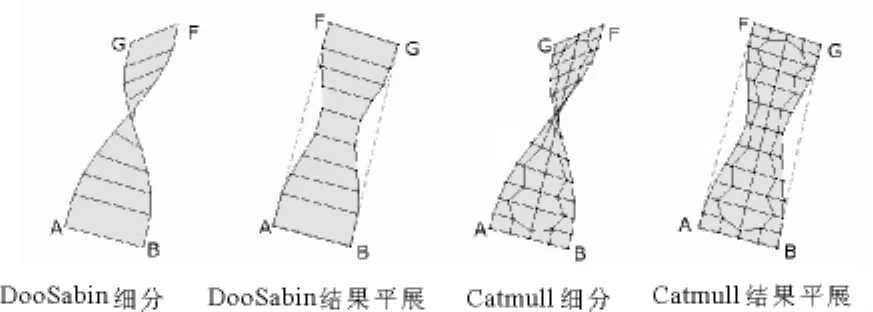
图2 含扭曲面片的网格细分变形

2 面片扭曲分析与检测

在图3中，未扭曲的四边形面片ABCD若沿中心轴旋转一圈则得到一个棱台;扭曲后四边形面片ABCD沿中心轴旋转一圈得到的立体是圆锥面的一部分.面片ABCD发生前述韧性扭曲的时候，我们期望它是沿棱台的表面产生扭曲，而经典细分给出的结果是按圆锥曲面进行扭曲的.

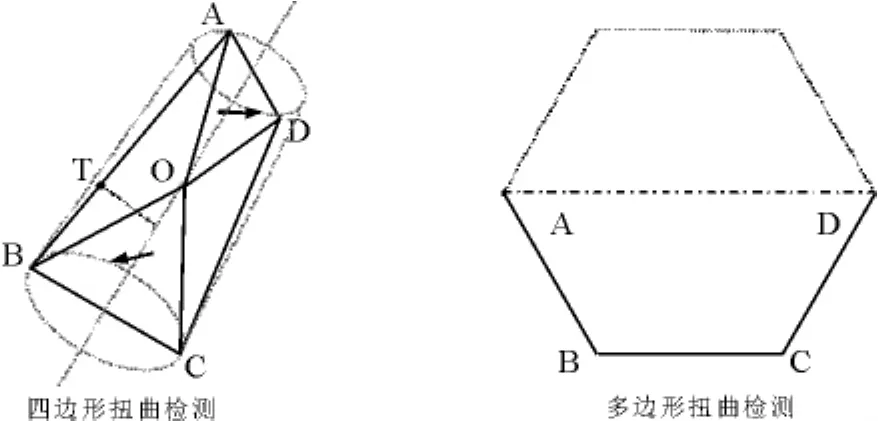
图3 多边形扭曲检测

一个面片是否发生扭曲，可以用相邻棱来判定.如图3中的四边形ABCD，它的AD边绕中心轴转动，带动面片发生扭曲.设该四边形几何中心为O，则在AD转动过程中，三角形BOC、AOD的形状保持不变，这两个三角形所在的两个面片之间的有序夹角恰好反映了当前面片的扭曲情况.设图中四边形ABCD的中心是O点，AD旋转了一定角度?，AB棱上随面片扭曲后的任意一点T，其细分位置是在某个圆锥曲面上的，根据棱台与圆锥之间的关系，可以按下式将T点从沿着圆锥曲面位置修正到沿着棱台曲面的位置:

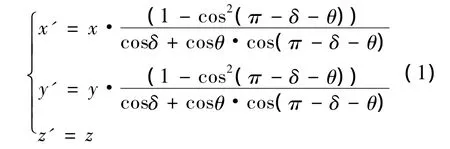
其中是两个相对棱的扭曲角度，为当前T点局部扭曲角度.

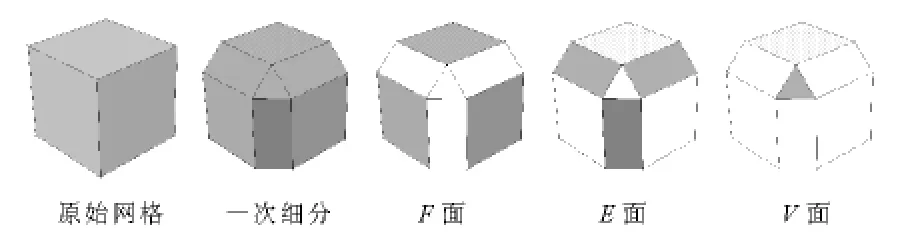
图4 经典Doo－Sabin细分过程

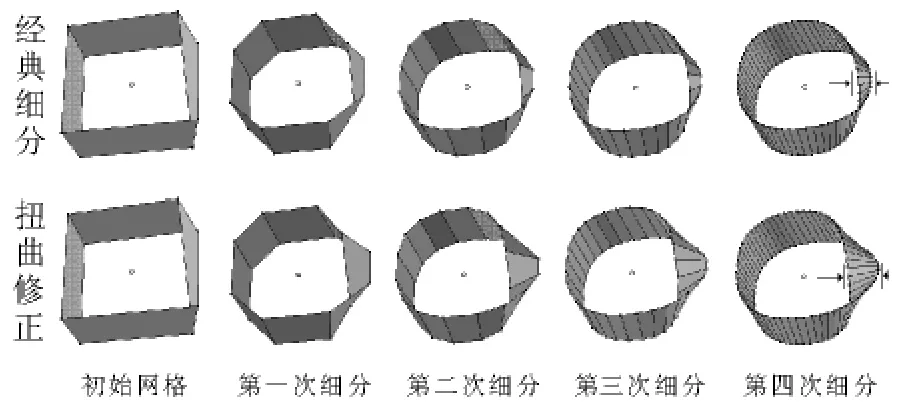
图5 Doo－Sabin细分与扭曲校正细分结果的对比

对于多边形面片，只要将目标棱及其两端的邻棱一起，构成一个四边形，就可以按照四边形的操作方法进行扭曲检测和对细分顶点进行校正，如图3中的多边形面片，当我们使用细分方法处理它的时候，在BC棱上，与棱BC相邻的分别是棱AB和棱CD，连接A、D构成一个虚拟四边形ABCD，若A与D重合，则ABCD是一个三角形面片，不需要处理;否则是一个四边形面片，这时按照前面所述处理四边形面片的方法进行处理即可.

下面以经典Doo－Sabin细分方法为例，详细介绍如何修改细分过程使之能恰当的处理含有扭曲面片的网格.

3 Doo－Sabin方法对扭曲面片的校正

经典Doo－Sabin细分方法简述:对于初始控制网格Mk，其中任意一个多边形Pk的顶点(0≤i≤n)，细分后对应的多边形为Pk+1，每个顶点生成对应的新的顶点:

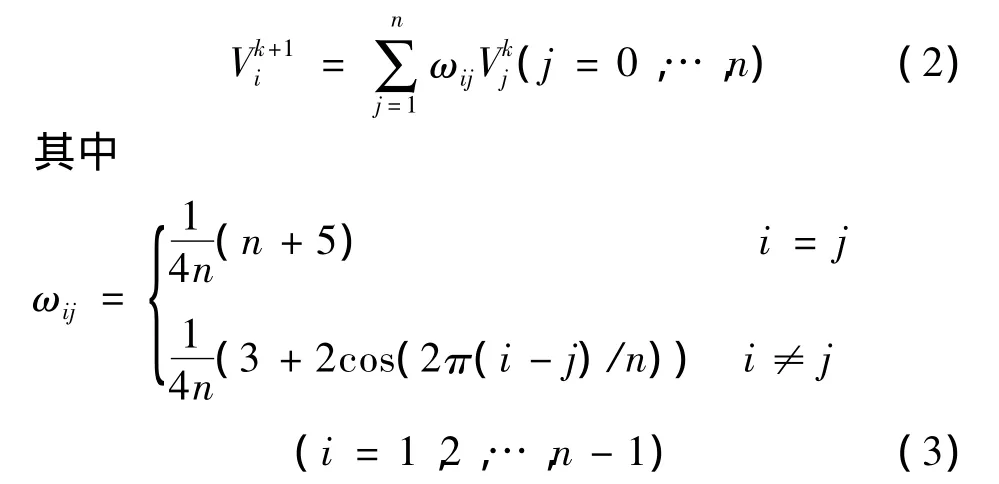
具体细分步骤:

(1)对初始控制网格Mk的每个顶点应用式(2)生成新的顶点;

(2)依次连接控制网格Mk的每个面中的所有新生成的顶点得到F面;

(3)依次连接控制网格Mk的每个边两边面所对应的新顶点得到E面;

(4)依次连接控制网格Mk的每个点新生成的顶点得到V面;

经典Doo－Sabin属于逼近型细分方法，具有良好的光滑性，当初始网格为正则四边形的时候，可以生成二次B样条曲面，在奇异点处至少可以达一阶连续.其中F面生成过程是内敛的，与外部面无关，我们可以在经典Doo－Sabin生成F面的(2)过程中加入对扭曲的检测，即对当前面片的每一条棱，检测与它端点相邻的棱是否为边缘棱(这个棱只有一个相邻面)，如果是边缘棱则按上节讨论进行扭曲判断与校正;否则棱有两个相邻面，这时交由细分方法进行正常处理.这里不讨论棱没有相邻面或者棱有多于两个相邻面等对于细分方法来说是病态网格的情况.

对于Catmull－Clark细分，只要在其第一次细分时应用上述方法对网格进行处理校正即可;LOOP细分也是在第一次三角化时应用上述方法对面片进行处理校正，这里不再赘述.

这里选择莫比乌斯面，分别使用经典Doo－Sabin细分和使用了扭曲校正的Doo－Sabin细分改进方法，得到图5的结果.

4 实际结果及分析

从图5可以看到，在图形右侧有显著扭曲的面片处，经典Doo－Sabin细分方法在处理显著扭曲面片时，扭曲处会收缩得非常窄(如图5中“第四次细分”上箭头标注);而在增加扭曲修正后，得到的面片基本符合期望的韧性扭曲特征.

此方法可以根据需要，在网格中存在显著扭曲而经典细分不能给出期望结果时对细分结果进行校正，且不会改变原细分方法的连续性和光顺性，所以原细分方法仍保持自己的连续性特征.

5 结论

从经典细分过程在空间网格中含有显著扭曲面片情况下会产生的不理想结果开始，详细讨论了问题形成原因及解决思路，给出了较通用的扭曲面片校正方法，此方法简捷有效易于实现，且可以集成到经典Doo－Sabin细分方法中使用而且保持原有的细分方法的光滑特性，在实践中得到了较好的结果.此外，该方法与其它细分方法的结合，还需要做进一步研究.

[1]Catmull E，Clark J.Recursively Generated B － spline Surfaces on Arbitrary Topological Meshes[J]Computer － Aided Design，1978，10(6):350 －355.

[2]Doo D，Sabin M.Behavior of Recursive Division Surfaces Near Extraordinary Points[J]Computer － Aided Design，1978，10(6):356－360.

[3]Loop C T.Smooth Subdivision Surfaces Based on Triangles[D].M.S.Thesis，Department of Mathematics，University of Utah，1987.

[4]Nira Dyn，David Levin.Subdivision Schemes in Geometric Modelling[EB]，1998.Israel Tel－ Aviv University 19 －23.

[5]Sederberg，T.，Zheng，J.，Swell，D.，Sabin，M.，Non － uniform Recursive Subdivision Surfaces.In Computer Graphics Proceedings，ACM SIGGRAPH，1998:387－394.

[7]张湘玉.保细节的基于曲面控制的网格变形[J].华南理工大学学报，2010，38:39 －44.