稀疏投影在目标跟踪中的应用

邵 洁

(上海电力学院计算机与信息工程学院，上海 200090)

运动目标分析是计算机视觉研究领域中的一个富有挑战性的课题.它涵盖了移动目标物体的检测、跟踪，以及跟踪物体的行为识别等多个方面的内容.一个鲁棒的视频跟踪算法需要克服噪音的影响，图像中的目标间互遮挡或物体对人的遮挡，图像视角变化，复杂的背景和光照变化等.

跟踪算法能够实现对一段时间内目标空间状态的估计.早期研究中，基础跟踪算法通常采用卡尔曼滤波实现.然而由于卡尔曼滤波只能提供状态变化服从线性高斯分布的目标最优值估计，不符合现实中的目标运动变化状态，使得其后产生的基于非线性模型的粒子滤波方法逐渐成为更广泛使用的次最优状态估计方法.在基础跟踪算法选定的情况下，如何利用特征找到与已有跟踪目标或模板最匹配的观测目标是目标跟踪的关键.

1 算法概述

本文尝试通过寻找模板子空间中目标的稀疏最优估计实现目标跟踪.这一设想来自于文献［1］，首先在第一帧初始化目标模板，然后在跟踪过程中，通过贝叶斯框架下的粒子滤波得到多个候选目标位置，再将候选位置的目标模块表示成目标模板的稀疏线性加权和.因此，处于最正确候选位置的目标模块应当最能有效地由目标模板表示.事实上，通过将这种表示转化为一个L1正则化最小二乘问题求解时，可以得到一个候选模块关于目标模板的稀疏权值向量.而与目标模板加权和差值最小的候选模块是当前帧的最优跟踪结果.其算法流程如图1所示.

图1 基于稀疏表示的目标跟踪算法基本流程

2 粒子滤波算法

粒子滤波是一种利用贝叶斯序列重要性采样技术来估计状态变量的后验概率密度分布的算法.它包含预测和更新两个基本步骤.假设xt表示描述t时刻物体特征的状态变量，则在已知所有1 到 t－1 时刻的观测结果 z1∶t－1={z1，z2，…，zt－1}的条件下，xt的条件预测分布为 p(xt/z1∶t－1):

而在t时刻，当已知观测值zt，则基于贝叶斯规则可以得到状态向量的后验概率密度为:

式中:p(zt/xt)——观测似然概率密度.

以100个采样粒子为例，在地铁视频中针对人群中某一目标得到以采样粒子为中心的候选跟踪模块分布，则相应的粒子权重更新为:

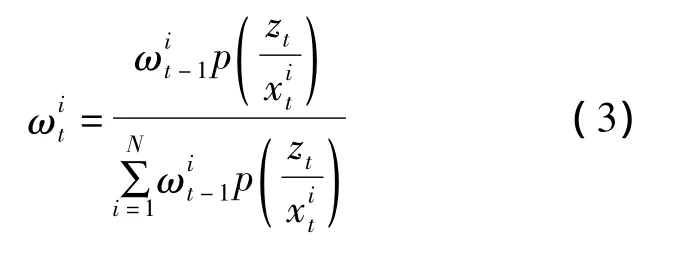
图2 粒子样本分布示例

在本文的跟踪算法中，采用图像的仿射变换以实现对连续两帧目标，运动建模.状态变量xt=(Λ，px，py，vx，vy)包括仿射参数向量 Λ，目标位置(px，py)和平均速度(vx，vy).仿射参数 Λ 来自于对已知状态xt的计算.首先从图像中获取感兴趣区域zt，并将其归一化为目标模板大小.本文假设状态转换概率 p(xt/xt－1)服从高斯分布，且仿射向量中各参数独立，则观测模型p(zt/xt)的大小反映了观测值与目标模板的相似程度.在跟踪过程中，p(zt/xt)由目标模板和观测值的L1最小化误差得到.

3 基于L1最小化的跟踪

在跟踪过程中，本文将不同光照背景和视角下目标的全局特征投影到一个低维子空间中来实现状态估计.若已知目标模板序列T={t1，t2，…，tn}∈Rd×n(d ＞＞ n)，包含 n 个 ti∈Rd的向量矩阵，则跟踪结果全局特征y∈Rd可以表示为:

式中:a——目标参数向量，a={a1，a2，…，an}T∈

在许多视频目标跟踪场景中，目标物体常常面临噪音或局部遮挡的问题，尤其遮挡会影响图像的任何位置或任意大小，会产生不可预测的检测错误.因此，考虑噪音和遮挡问题的影响，式(4)可以写成:

式中:ε——非零错误向量，表示y中被遮挡或破坏的像素.

事实上，由于ε的不确定性，a有无数种不同的解.然而，一个可信的目标跟踪模块应当在其对应向量a中只存在有限个数的非零值，也就是说，目标跟踪模块仅可能与有限个目标模板有较高的相似性.因此，将式(5)转化为一个L1正则化最小二乘问题，即:

式中:‖·‖2，‖·‖1——L1和L2范数计算.

L1正则化最小二乘问题可通过Lasso问题求解法得到解决，本文直接采用 INRIA提供的SPAMS稀疏分解工具箱加以实现.

4 模板更新

在计算机视觉中使用模板跟踪方法始于1981年［2］.首先在第一帧中提取目标模板，在随后每帧中感兴趣的区域找到最为匹配的目标位置.一个固定的目标模板不足以应对视频中可能产生的变化，而如果模板随视频更新过快易导致丢失原始目标状态而仅保留包含更多不确定性的跟踪信息.

本文采用的基于稀疏表示的目标跟踪法与传统的模板匹配法有类似之处.虽然在初始时间内，目标外表会保持不变，但随着时间的延续，模板与目标的当前外表会出现差异，这与目标行为和面对摄像机的角度有关.因此，我们采用目标模板T的动态更新来解决这一问题.

L1最小化的一个重要特点是模板的范数越大，最小化得到的差值越小，这是由式(6)中‖a‖1项的存在产生的.模板‖ti‖2的值越大，‖Ta－y项中相对应的系数ai越小.利用这一特性，可以引入一个与每个模板相关联的权重向量ωi=‖ti‖2.权重越大，表示模板与当前目标的相关性越大.第一帧中，人为选定模板并对其进行归一化.对选定模板模块上下左右略微移动一定像素值可以得到多个不同的模板，提取特征后可以得到模板矩阵.

初始条件下，每个模板的权值ωi相同，都等于1.每一帧结束后对权值进行更新后就可得到:

若当前目标与最优模板的相似度大于某一阈值，则调整每个模板的范数‖ti‖2=ωi，并对其进行归一化;若两者相似度小于某阈值的话，则将相似度最低的模板更新为当前目标特征，其权重值初始化为所有权重的平均值.

5 实验结果与分析

在Matlab环境下，采用大量的视频对其进行了有效性测试.

实验环境:双核2.66 GHz CPU，3 GB内存，帧图像为768×576像素，视频跟踪算法运算速度为每秒4帧.

测试视频包括室内外大量不同人流密度的场景，且场景中包含光线变化和不同程度的遮挡.实验以第一帧为参考帧，即所取的模板均取自第一帧的目标模块.每一个目标分配20个不同模板.这些模板的获取同样来自于第一帧的目标模块，仅在原始位置的不同方向微移后选取.在所有情况下，初始位置和目标的选取均由人工实现，粒子数量固定为400.

采用本文的跟踪方法实现的跟踪效果如图3所示.每一行从左往右排列5帧同一场景的跟踪效果图片，图片的左上角显示的数字表示当前帧数.每张图片均标注了从起始帧到当前帧被跟踪目标的运动轨迹，显示了跟踪方法在各种场景中捕获运动变化的持续时间的有效性和稳定性.第1行的图片序列显示了在拥挤的机场候机室中，跟踪一位身着深色上衣的旅客的过程.这位旅客从一排椅子的右侧绕行至左侧，并穿过了一群向相反方向行走的人.这种单一目标的无规律运动变化是无法由运动流模型［3，4］模拟得到的.第2行图片序列显示了对广场上人群的俯视拍摄.虽然被跟踪行人身着的灰色上衣近似于地面颜色，但仍能被正确跟踪，显示出本算法对于相似颜色条件下的跟踪仍可保持较高的精确性.第3行图片序列来自于2009年的PETS测试图库，显示了一群人在校园中从西向东行走的场景.由于镜头较远，因此人在图片中所占比例较小，很难捕获人物的具体细节特征，同时地面上斑驳的树影显示出场景的光照条件比较复杂.第4行图片序列展示了地铁楼梯上的异常拥挤场景，人流由上至下缓慢行走，画面中大多为黑色和白色，人与人之间特征差别较小.

在所有这些具有挑战性的场景中，本文提出的方法均能稳定地跟踪到目标.

图3 算法跟踪效果示意

6 结语

本文提供了一种稀疏表示算法在实际场景中目标跟踪的实现方法.可将跟踪过程看作一个稀疏估计问题，并采用L1正则化最小二乘法对其求解.为了适应目标的变化，还引入了动态模板更新算法.

经过对多例实际场景视频的跟踪实验，均获得良好的跟踪效果，尤其是具有良好背景分割效果的视频，可以得到准确的跟踪结果.实验表明，该算法具有良好的鲁棒性.但该算法的计算时间花销过大.相信随着计算机的发展、程序的优化，这一问题将会得到解决.

［1］MEI X，LING H.Robust visual tracking and vehicle classification via sparse representation ［J］.PAMI，2011，33(11):2 259-2 272.

［2］LUCAS B，KANADE T.An iterative image registration technique with an application to stereo vision［C］//ICJAI，1981:674-679.

［3］RODROGIEZ M，ALI S，KANADE T.Tracking in unstructured crowded scenes，computer vision［C］//2009 IEEE 12th International Conference on Kyoto， Japan， Sep.， 2009:1 389-1 396.

［4］ALI S，MUBARAK Shah.Floor fields for tracking in high density crowd scenes［C］//ECCV’08 Proceedings of the 10th European Conference on Computer Vision，Marseille，France，2008:1-14.