基于改进BP神经网络算法的短期负荷预测

潘雪涛

(上海电力学院电力与自动化工程学院，上海 200090)

准确的短期负荷预测是电力调度部门的重要工作之一.目前，短期负荷预测方法大致可分为传统方法和智能方法两大类.传统的短期负荷预测方法以趋势时间序列法、外推法、灰色模型法等为主，这些算法原理简单、速度快，但难以表达负荷与其影响因素的非线性关系，从而限制了其在短期负荷预测中的应用［1-3］.智能方法主要包括专家系统、人工神经网络和支持向量机等，其中，人工神经网络以其强大的自主学习能力、非线性处理能力等特性，较好地克服了传统方法中的某些缺点［4，5］，但在实际运用中还存在着网络结构选择困难、泛化能力较差、易陷入局部极小、收敛慢等缺陷［6，7］.

本文进行了改进BP神经网络算法的研究，并利用基于Matlab语言的优化计算程序，结合某电网负荷数据进行短期电力负荷预测仿真，比较分析了改进方法在计算速度与预测误差方面的优势.

1 BP神经网络

1.1 BP神经网络的特点

BP学习算法的前向网络是当前应用最为广泛的人工神经网络之一，可以解决神经网络面临的许多问题.BP神经网络算法一般可描述为正向的信号输入过程和误差信号反向传播过程.反向传播算法通常采用梯度法修正权值，因此要求输出函数可微，通常可选择Sigmoid型函数作为激励函数.

给定任意一组输入样本数据，采用BP网络进行训练，各层之间的映射关系存储在连接权值和阈值上.网络的实际输出与期望输出之间的差值即为误差信号，误差信号从输出端开始逐层向前传播，在误差信号反向传播的过程中，网络的权值由误差反馈进行调节.通过权值的不断修正使网络的实际输出逐渐接近期望输出.该算法类似梯度下降法，不同的是BP神经网络算法是将人为选取的一个常数作为学习率，这样处理虽然便于简化计算，但也带来一些问题.如果步长较小，可能会造成计算效率低，收敛速度慢;如果步长较大，向前一步可能跨过了最优点，而后退一步又可能回到原点，这样就会产生振荡现象.因此，BP网络学习率的大小对学习算法具有重要影响［8，9］.

1.2 BP神经网络算法的改进

基于上述问题，目前已有很多研究提出了有效的BP网络算法的改进，主要有以下两种.

(1)变步长法 该方法权值的修正方法为:

这里的权值修正方法与连续两次迭代的梯度有关.若连续两次迭代的梯度方向相同，表明下降太慢，这时可将步长加倍;若连续两次迭代的梯度方向相反，表明下降过头，这时可将步长减半.该方法的不足之处是步长调整幅度太大容易引起振荡.

(2)变尺度法 常规BP算法采用的是一阶梯度法，因而其收敛速度较慢.若采用二阶梯度法则收敛速度会有较大的提高，但二阶梯度法计算很复杂.变尺度法是对二阶梯度法的简化计算，但其计算相对来说还是较为复杂［10-12］.

本文采用变步长的改进BP算法，采用批处理方式，即每一个样本对网络并不立即产生作用，而是等到一个训练周期的全部输入样本都依次输入后，将全部误差求和累加求出总的误差，然后集中修改权值.置各权值或阈值的初始值为小的随机数值，具体步骤如下.

(1)设置初始权值W(0)和V(0)为较小的随机非零值，并输入其他网络参数，误差E置0，学习率η设为0～1内的小数，网络训练后达到的精度Emin设为一小的正数.

(2)提供训练样本，输入向量为X=(x1，x2，…，xn)T，期望输出向量为 d=(d1，d2，…，dn)T，然后对每个输入样本进行步骤(3)到步骤(5)的迭代.

(3)计算网络的实际输出及隐层单元的状态.

(4)分别计算输出层和隐含层的训练误差.

(5)保存当前样本的训练误差Ek，到步骤(2)继续迭代，直到本次样本结束.

(6)计算样本训练的总误差，并加以判断，若E(t)＞E(t－1)，则按η=η/2减小学习步长.根据总误差E=∑kEk，修正BP网络的权值，否则转至步骤(7).

(7)按η=2η增加学习步长.

(8)根据总误差E=∑kEk，计算 BP网络的权值.

(9)判断误差是否满足要求，不满足转至步骤(2)，满足则结束.

2 负荷预测改进BP网络设计

2.1 输入变量的选取

负荷曲线是与很多因素相关的一个非线性函数.对于抽取和逼近这种非线性函数，神经网络法是一种合适的方法.神经网络输入变量的常见选择方法有自相关系数法、正交最小二乘法、相空间重构法等［13，14］.文献［3］分析了影响负荷各因素的相关特性，结果表明，预测日前一天、前两天、前一周的同一时刻及前一天和前两天预测时刻的前一个时刻、前两个时刻的历史负荷与预测负荷有较强的关联.

神经网络的优点在于其可以模拟多变量而不需要对输入变量做复杂的相关假定.本文采用的是美国加州电力市场2000年4月30到2000年6月6日的日负荷小时值［7］.

2.2 数据归一化处理

式中:Xmax，Xmin——训练样本输入变量的最大值和最小值;

Pi，Xi——输入样本归一化前后的值.

为了避免出现神经元饱和现象，需要在输入层用式(4)将负荷数据换算成［0，1］区间的值，再在输出层用式(5)换算回负荷数据.

2.3 网络结构

从理论上来说，根据多层感知器的特点，增加隐层数以及每层节点数可以提高神经网络的非线性处理能力.但实际应用中，并非隐层数越多或节点数越多，拟合优度就越好，而往往是根据经验在训练误差与拟合误差之间权衡.一般认为，符合样本特性的最简单的网络结构预测效果最好［8，9］.

本文采用单隐层BP网络，隐层节点数用试错的办法，由少到多训练并检验网络的性能.考虑到收敛速度，节点数选取由式(6)和Kolmogorov定理确定［11］:

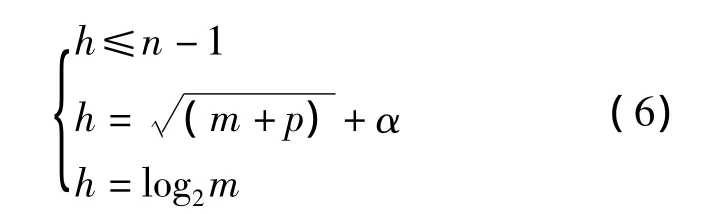
式中:h——隐含层节点数;

m——输入层节点数;

p——输出层节点数;

α——0～10之间的常数.

经过检验，本文采用的网络结构:输入节点个数为6;隐含层节点个数为10;输出节点个数为1.

2.4 负荷预测误差指标

由于负荷预测是一种对未来负荷的估算，因此它与客观实际存在着一定的差距，即预测误差.计算误差的方法很多［10-14］，本文选用相对误差(RE)来分析负荷预测误差:——

式中:Xi， 第 i时刻的实际负荷值和预测值.

3 算例分析

本文利用美国加州2000年的负荷数据进行仿真预测［7］.截取2000年4月30日到6月4日作为输入数据，以6月5日数据为期望输出进行训练，用Matlab 2009工具箱对6月6日24 h负荷值进行预测.表1给出预测日相对误差平均值，作为对比，将常规BP神经网络方法同时刻训练样本集的相应预测结果也列于表1.

表1 预测结果及误差

仿真结果表明，常规BP神经网络方法预测的最大误差为5.245%，平均绝对值相对误差为2.273%;改进BP神经网络方法预测的最大误差和平均绝对值相对误差分别为 5.925%和1.261%.由此可见，改进BP神经网络方法预测的平均相对误差比常规方法降低了0.445%，其预测精度有所改进.而且对于每个点的预测模型，改进BP算法训练周期在500以内，比常规BP算法训练速度快.

4 结论

(1)改进BP神经网络算法可以避免接近最优点时产生波动和振荡现象，负荷预测精度有所提高，这主要是因为学习速率可根据需要达到充分小.

(2)改进的BP神经网络算法速度快、精度高，可用于短期电力负荷预测，具有一定的实际应用价值.

［1］甘文泉，胡保生.用自适应神经网络进行短期电力负荷预测［J］.电网技术，1997，21(3):28-31.

［2］罗治强，张焰，朱杰.中压配电网中长期负荷预测方法研究与应用［J］.华东电力，2003，31(1):9-12.

［3］CHOW T W S，LEUNG C T.Neural network based shortterm load forecasting using weather compensation［J］.IEEE Transactions on Power Systems，1996，11(4):1 736-1 742.

［4］VOGL T P，MANGIS J K，RIGLER A K，et al.Accelerating the convergence of the back propagation method［J］.Biological Cybernetics，1988，59:257-263.

［5］OSMAN Z H，AWAD M L，MAHMOUD T K.Neural network based approach for short-term load forecasting［C］//Power Systems Conference and Exposition，2009:1-8.

［6］周德强，武本令.灰色BP神经网络模型的优化及负荷预测［J］.电力系统保护与控制，2011，39(21):65-69.

［7］敖磊.电力市场短期电价预测模型及研究［D］.武汉:华中科技大学，2006.

［8］MATLAB中文论坛.MATLAB神经网络30个案例分析［M］.北京:北京航空航天大学出版社，2010:21-54.

［9］朱楷，王正林.精通MATLAB神经网络［M］.北京:电子工业出版社，2010:193-224.

［10］白连平，陈秀真.提高BP网络学习速度的自适应算法［J］.系统仿真学报，2001，8(13):97-98.

［11］李莉，孔哲峰，李鹏，等.专家系统与BP神经网络相结合的短期负荷预测［J］.陕西电力，2009，37(1):22-27.

［12］LING S H，LEUNG F H F，LAM H K，et al.Short-term electric load forecasting based on neural fuzzy network［J］.IEEE Transactions on Industrial Electronics，2003，50(6):1 305-1 316.

［13］SENJYU T，TAKARA，H，UEZATO，K，et al.One-hourahead load forecasting using neural network［J］.IEEE Transactions on Power Systems，2002，17(1):113-118.

［14］SATISH B，SWARUP K S，SRINIVAS S，et al.Effect of temperature on short term load forecasting an integrated ANN［J］.Electric Power Systems Research，2004，72(1):95-101.