基于遗传算法的潜艇自航模水声定位系统定位站布置研究

张文照，肖昌润，刘瑞杰

（海军工程大学，武汉 430033）

1 引 言

参数辨识结合水下自航模试验技术，在获得潜艇耦合水动力系数和研究大机动条件下的潜艇操纵性有着独特的优势。由于自航模处于潜航状态具有光学不可观测性，因而水声定位技术是获取自航模水下运动轨迹的唯一方法[1]。该方法的测量误差与定位站的几何布置有着密切的关系，在一定的约束条件下，如何获取一个精度相对较高的定位站布置是一项关键的技术，对于这个问题的研究目前在国内开展不多，主要是因为优化变量数目多，目标函数不易表达。本文通过遗传算法，尝试优化了不同模型下水听器的布阵形式。

2 试验中实际问题及优化模型的提出

由于自航模试验属于外场试验，因而在试验中，水听器的布放会受到自然场地的限制。本文所讨论的试验场自然场地如图1所示。综合考虑试验条件的限制与试验精度的要求，将试验中实际的水听器布放方案抽象为如下数学模型（如图2所示，图中线段AB代表水坝，C点代表试验基地，斜线部分为由试验条件限制决定的水下水听器布放区域）:方案一:AB之间布置2个水听器，C点处布置1个水听器，水下布置1个水听器；方案二:AB之间布置2个水听器，水下布置2个水听器；方案三:AB之间与C点各布置一个水听器，水下布置2个水听器。由于水下水听器位置的最优解可能出现在边界附近，为了在优化算法中能方便地处理边界条件，因此以C点为极点，岸边方向为极轴，建立柱坐标系，将水下水听器在该坐标系中的极径ρ和极角θ作为优化变量。该数学模型的具体表达如表1所示。

图1 试验场实际情况Fig.1 Environment of test field

图2 抽象出来的数学模型Fig.2 The math model

表1 优化模型数学表达Tab.1 Mathematical expression of optimization models

其中，当在水底布放2个水听器时，这两者是等效的，为了出现避免出现重复解，人为的加上边界条件令其中一个的y值大于另一个。另外根据已有的研究，同步式水声定位的几何精度和目标位置距到基站位置的矢量两两之间的夹角相关，总体而言，夹角越大则精度越高，根据几何上得大角对大边的定理，也就是各基站之间的连线越长则定位精度越高，因此对于水坝上布置两个水听器的情况，人为地将其布置在A、B两点。

3 基于GDOP指数的目标函数的提出

它反映了给定阵型空间各点的定位误差随基站几何关系的水听器测距误差放大系数。对于给定的定位问题，如果将定位区域均匀划分一定数量的网格，设定某一误差限σ0，统计出区域中所有GDOP值小于σ0的网格节点的个数，即可以评判出这种水听器布阵方式的优劣，定义这些点个数与总的网格数的比值为阵型性能指数C。为了验证阵型性能指数用来衡量阵型性能的有效性，可以选择一个已知最优阵型和另外2个对比阵型分别计算它们的阵型指数，并比较结果。由于无约束条件下，当4个水听器的测距误差相同的情况下，4点定位的最优阵型为正四面体，因此构造尺寸为200×173×163的计算域，以计算域的一个边构造出一个正四面体，使该四面体的一个面与立方体的下底重合，将水听器布置在四面体的四个顶点上作为阵型1。在阵型1的基础上移动四面体底面所对的顶点处的水听器来构造阵型2和阵型3（见图3），各水听器的误差都设置为1，则平均误差σm=1，设定误差限为5σm，10σm和15σm，分别计算不同的阵型性能指数，结果如表2所示。

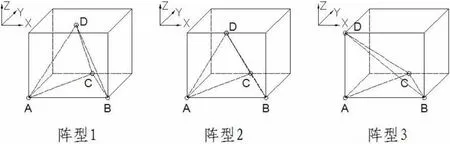
图3 用于验证的三个特定阵型Fig.3 Three specific arrangements for validation

表2 不同阵型的阵型指数Fig.2 Arrangement Index for different arrays

由已知理论[2]阵型1是最优的，计算结果符合这一结论，同时减小误差限可以提高最优阵型与其他阵型之间阵型性能指数的差异，更利于优选出最优阵型。本文中的计算选择误差限为5σm。

实际问题中因为水下布放的水听器的位置不能通过精度相对较高的GPS定位来得出，因此其测距精度要比岸边布置的水听器差一些，通过试验中的标定，设定计算中岸边水听器的测距精度误差σ=0.01 m，水下水听器的测距精度为σ=0.03 m。

综上所述，本文的优化问题的目标函数可以描述为:

其中Xi为定位水听器位置坐标，xi为网格节点坐标，F（xi）=0为边界条件，count为计数函数。

4 本文采用遗传算法的建立

遗传算法是以生物进化理论为基础，并结合计算机的快速迭代技术而发展起来的全局搜索优化算法；它显著的优点是优化的对象无严格的解析式要求，同时也适合于各种变量形式特别是离散变量，并且能优化得到全局最优解。经过若干代的选种、杂交、变异、繁殖操作后，便可得到较优良的改进解[3]。

4.1 优化问题特点分析

水听器布阵位置的优化实际上是在一定的空间区域里探索点的坐标的过程。为了方便最优解的探索过程，因而选用实值种群，种群中每个个体由优化变量实际取值组成，其重组过程采用中间重组策略，其物理意义为从选定交叉的两个父代点所组成的扇形区域里随机产生两个子代点（参见图4）。

为了防止优化结果收敛于局部极值，变异的加入也是很重要的，对于实值种群的变异，其物理意义为在变异点附近产生一个新的点（参见图5）。

图4 实种群的重组Fig.4 Real population’s recombination

图5 实种群的变异Fig.5 Real population’s mutation

本文采用了精英保留政策，第一步选择90%的个体参与新的个体的产生（即代沟为0.9），第二步，对选择出的个体实施交叉，变异运算；第三步，将父代中前10%的最优的个体插入到上步所产生的种群中，形成子代个体。上述操作过程可以通过以下的伪代码予以描述:

4.2 边界条件的处理

对于优化模型中的几何边界，本文采用惩罚函数的方法，即如果种群里点的坐标出现x<30或者y<30中的任何一种情况，目标函数值则取0。对于为了避免出现重复解而人为设定的条件，则在每执行一步遗传运算的同时加入判断环节，即判断如果第一个点的极径小于第二个点那么就将两者易位。

5 三种模型的优化结果

5.1 优化模型1的优化与遗传算法的验证

对于优化模型Ⅰ，可以将水下水听器要布放的平面区域离散化，求出离散后各网格点所对应定位阵型的阵型指数，在其中寻找阵型指数最大的一个点，从而近似得到优化模型Ⅰ所对应问题的最优解（如图6所示），并且离散网格划分得越细，通过这种方法得到的数值最优解越接近真实解。

如果将上述方法得出的最优解与通过遗传算法得出的最优解予以比较的话，即可以验证遗传算法的有效性。经过数值模拟，可以得到模型Ⅰ问题最优点坐标为（182.75，79.45），最佳的阵型系数为0.1656，通过遗传算法得到的最优点为（177，78.20），最佳阵型系数为0.1659，最佳布阵型式的俯视图如图7所示，可以分析出，数值模拟和优化的结果不同的原因是数值模拟的网格节点不够精细，最优点与网格节点不重合。同时也可以得出结论，这种遗传算法的优化程序在优化水听器布阵型式的问题上是适用的。

图6 优化模型Ⅰ的数值模拟Fig.6 Numerical simulation for optimization modelⅠ

图7 优化模型Ⅰ遗传算法计算结果Fig.7 GA’s result for optimization modelⅠ

5.2 优化模型Ⅱ、Ⅲ的优化与结果分析

模型Ⅱ、Ⅲ的优化结果见表3。

表3 模型Ⅱ、Ⅲ遗传算法优化结果Tab.3 GA’s result for optimization modelsⅡ andⅢ

模型布阵型式的俯视图参见图8。图中，A，B点为岸边布置的水听器，他们之间的连线简称为岸边基线，C，D点为水下水听器布置位置在水平面上的投影，O点为定位区域的中心点，虚线为岸边两水听器之间连线的中垂线（为方便叙述，以下简称基线中垂线），双点划线为过O点与上述中垂线平行的直线（为方便叙述，以下简称中心中垂线）。下面就其结果予以分析。

从结果可以看出，十字阵为最佳的定位阵型，该十字阵由岸边两水听器之间连线为一边，以水下水听器连线为另一边交叉而成，这与目前研究文献中所述的一致。同时，水下水听器应该布置在两个岸基水听器的中垂线附近，但由于要考虑整体区域的定位效果，它们应当向中心中垂线偏置，其中一个距离岸边较近，出现在边界上，另外一个则需要布置在距离岸边基线200 m（这个距离应该是由约束条件和水听器定位精度决定的）附近，对于模型Ⅲ，D最远距离岸边基线只能达到161.26 m，因此D点出现在边界上。

图8 优化模型Ⅱ、Ⅲ遗传算法计算结果Fig.8 GA’s result for optimization modelⅡ andⅢ

5.3 模型之间互相比较及分析

由于模型Ⅰ与模型Ⅱ、Ⅲ的水听器平均定位精度不同，不能直接予以比较，因此设定模型Ⅰ的截止误差与模型Ⅱ、Ⅲ相同重新计算其阵型指数。结果如下表4所示。

表4 设定截止误差相同后最优阵型的阵型指数Tab.4 Arrangement Index of three optimum arrays after adjusting limitation error

可以看出，水下布置2个水听器比水下布置1个水听器而言具有较大优势。模型Ⅲ较模型Ⅱ来说，由于其岸边基线长度较大，因而定位精度精确不少。通过数值模拟可以得到3种模型的GDOP空间分布切面图，从中可以看出，对于模型Ⅲ的布置方式，空间中各点的定位精度都较高，这与阵型指数所描述的也是一致的（如图9所示）。

图9 三种模型最优布阵的GDOP分布切片图Fig.9 GDOP slice graph for three optimum array

6 结 论

通过本文的研究，可以得出如下结论:

（1）建立一种优化水听器布阵的算法，并且通过一个特殊的算例予以验证。

（2）通过对计算结果的分析，说明了4个水听器定位的情况，十字阵为最佳布阵型式，其中岸边基线的长度对定位精度的影响较大，基线越长定位精度越高。

（3）在今后的布阵工作中可以采取如下方法:首先在岸边选取距离尽量远的点布置两个水听器作为岸边基线，之后在该基线的中垂线附近布放水下水听器。具体位置可以通过遗传算法算出。

（4）可以看出4点定位的精度受岸边基线长度和水下水听器距岸边基线距离影响较大，其中的关系可以进一步研究。

[1]王 波,毕 毅.水声式自航模运动轨迹实时测量系统[J].船舶工程,2003(2):13-17.

[2]孙仲康.定位导航与制导[M].北京:国防工业出版社,1987.

[3]雷英杰.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.