复系数奇异Sturm－Liouville方程的极限点判定

景海斌 邓全才 岳崇山

(1.河北建筑工程学院，河北张家口075000;2.河北北方学院理学院，河北 张家口075000)

0 引言

其中p(t)=p1(t)+ip2(t)≠0，q(t)=q1(t)+iq2(t)是复值函数，w(t)是一个权函数，并在［0，+∞)上几乎处处大于在［0，+∞)上局部可积，λ∈ℂ 是一个谱参数.为表达方便，记早在1910年H.Weyl就对方程(1)为实系数的情形进行了讨论，并给出了方程的一个分类:极限点型和极限圆型.若对任何λ∈ℂ，方程(1)的任一解y∈，则称方程为极限圆型，否则为极限点型.之后出现了许多关于极限点和极限圆的判别准则(如［1，p1552－1560］).对于复系数情况的讨论开始于Sims的研究(见［2］)，之后B.M.Brown等人给出了方程(1)的Sims分类:极限点1型、极限点2型和极限圆型(见［3，定理2.1］).本文将给出方程(1)为极限点1型的判别准则.

1 Sims分类

1.1 预备知识

由此可定义半平面

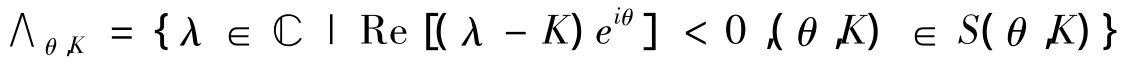
这里 δλ是 λ 到边界 ∂ ∧θ，K的距离.易证对(θ，K)∈ (θ，K)，有

1.2 Sims分类

下面给出复系数奇异 Sturm－Liouville方程(1)的Sims分类(见［3，定理2.1］)，对λ ∈∧θ，K，方程(1)有三种情形可能出现:

1)(1)存在唯一的解满足(3)，并且它也唯一属于，此时称方程(1)在∧θ，K上属于极限点1型;

2)(1)存在唯一的解满足(3)，但所有的解属于，此时称方程(1)在∧θ，K上属于极限点2型;

3)(1)的所有解均满足(3)，从而也都属于，此时称方程(1)在∧θ，K上属于极限圆型.

注1 此分类与半平面∧θ，K有关，但利用常数变异法易证，若对某个λ0∈ℂ，(1)的所有解均属于，则对任意λ∈ℂ，(1)的所有解均属于，即极限点1型不依赖于∧θ，K.

2 极限点1的判别准则

为给出本文的主要结果，需用到下面的引理.

引理 设(θ，K)∈S(θ，K)，则对 λ ∈∧θ，K，方程(1)至少有一个非零解y(t，λ)满足当t≥N时，有|p¯yy＇|＞l，其中N，l为大于零的常数.(见［4］，引理2)

定理1 若存在常数k1，使得p1(q1－k1w)≥0，p1≠0，且，则方程(1)是极限点1型的.

证明 不妨设p1＞0，令K0=k1+ik2，取θ=0，则由条件可知Re［rp(t)eiθ］=rp1≥0，Re{［q(t)－K0w(t)］eiθ}=q1－k1w≥0，故(0，K0)∈S(θ，K)，即0∈A(θ).设y=y(t，λ)为满足的方程(1)的非零解，下证y∉.

若不然，假设y∈L2w，由引理知|p¯yy＇|＞l＞0(t≥N)，再由Schwartz不等式，当t→∞时有

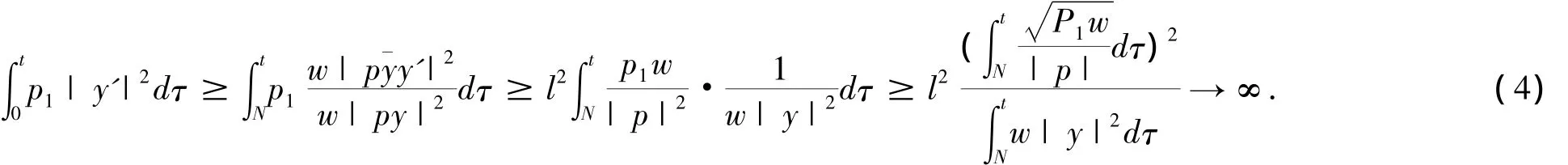
对以上等式两边从0→t积分并取实部，再由式及定理条件可得

故由(4)，(5)式知，存在0＜d＜1，使得

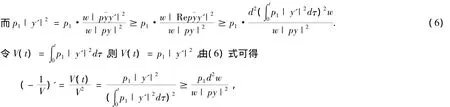
两边从N→t积分，再由Schwartz不等式得

这与(4)式矛盾，故y∉，而由注1知极限点1型不依赖于∧θ，K，故(1)为极限点1型.当p1＜0的情形，取θ=π，运用完全相同的方法可证明结论的正确性.

注2对于方程(1)为实系数的情况，当p(t)≡1，w≡1，若q有下界，则方程(1)必为极限点型(见［5，定理10.1.4］)，故此定理包括了实系数的相应判别准则.

定理1 是通过系数p(t)，q(t)的实部给出判别准则的，类似可得利用p(t)，q(t)的虚部也可得到相应结论.

定理2 若存在常数k2，使得，则方程(1)是极限点1型的.

证明 本定理也分p2＞0和p2＜0两种情况证明，并分别取运用和定理1类似的方法可证明本定理.

例 考虑方程－y"+(t2+1+it3)y=λy，t∈［0，+∞).

这里p(t)=w(t)≡1，q(t)=t2+1+it3，取k1=1，有p1(q1－k1w)=t2≥ 0，t∈［0，+∞).且，因此由定理1可知此方程为极限点1型.

［1］Dunford and J.T.Schwartz.Linear operators(II)［M］.New York:Wiley－interscience，1963

［2］A.R.Sims.Secondary conditions for linear diffeRential operators of the second order［J］.J.Math.Mech.，1957，6:247～285

［3］B.M.Brown，D.K.R .McCormack，W.D.Evans and M.Plum.On the spectrum of second－order diffeRential operators with complex coefficients［J］.Proc.R.Soc.Lond.Ser.，1999，A(455):1235 ～1257

［4］景海斌，綦建刚，岳崇山.复系数奇异Sturm－Liouville方程的极限点和极限圆分类［J］.数学物理学报，2010，30A(6):1534～1541

［5］E.Hille.LectuRes on ordinary diffeRential equations［M］.London:Addison－Weyl，1969