平衡辐射统计理论的探讨
胡同瑞,夏遵义,刘永皓
(大庆师范学院 物理与电气信息工程学院,黑龙江 大庆163712)
在量子力学建立初期,维恩根据经典理论求出了平衡辐射的能量密度与频率和温度的依赖关系,即维恩公式,但维恩公式在高频率段与实际符合的很好,在低频段出现严重的缺陷。二十世纪初期,瑞利同样用经典理论也求出了上述关系公式,后经金斯的补充,得出瑞利-金斯公式,但瑞利-金斯公式只适用于低频段,对高频段存在严重缺陷。在二十世纪初期,普朗克把平衡辐射当作光子气体,光子的自旋量子数为1,在动量方向上的投影为±h,有两个可能的值,相当于左、右两个方向的偏振。得出了无论在高频段或低频都正确的结论,即普朗克公式。
1 平衡辐射的经典理论
1.1 平衡辐射的圆频率
空间内的平衡辐射场可以分解为无穷多个单色平面波,电场强度用ε表示,如果采用周期性边界条件,单色平面波的电场分量为(由电动力学可知)[1]
ε=ε0ei(kr-ωt)
其中ω是圆频率,k是波矢。
根据连续性方程
(1)
其中拉普拉斯算符
(2)
将ε=ε0ei(kr-ωt)代入上式得

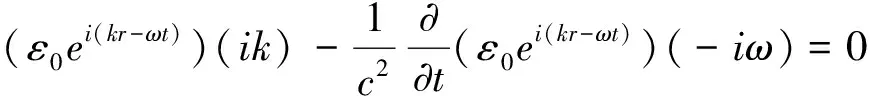
解得
ω=ck
这就是圆频率与波矢的关系。
1.2 瑞利-金斯公式
设波矢k的三个分量为kx,ky,kz,则可能值为[2]
解出nx,ny,nz
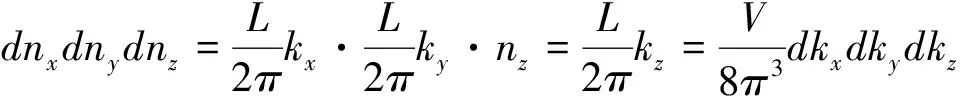
由于n为量子数,nx,ny,nz相乘应是量子态的数量。
k1=ksinθ,dθ=kdθ,dφ=ksinθdφ,dkxdkydkz=dθdφdk=k2sinθ·dθ·dφ·dk
对sinθ·dθ·dφ积分得
因此
dkxdkydkz=k2sinθ·dθ·dφ·dk=4πk2dk

由于平面波有两个偏振方向,上式要乘以2,则偏振数为
又根据圆频率与波矢的关系ω=ck

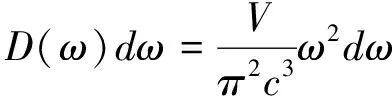
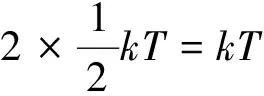
所以辐射场的能量为
(3)
这结果叫瑞利-金斯公式。
1.3 瑞利-金斯公式的缺陷
对瑞利-金斯公式积分
当频率趋于无穷大时,其积分值也趋于无穷大是不对的。不可能电磁波的能量随频率的增大而无穷地增大,这种错误的原因是电动力学辐射场具有无穷多个振动自由度,而推导过程中又根据经典统计的能量均分定理,每个振动自由度的能量为kT。由此可见,经典物理存在根本性的错误。
2 普朗克的量子理论
2.1 平衡辐射的可能状态数
普朗克把平衡辐射看作光子气体。光子的自旋量子数为1,在动量方向上的投影为±h,有两个可能的值,相当于左、右两个方向的偏振。为简单起见,我们首先讨论一维情况。设平衡辐射处在长度为L的一维容器中,其德布罗意波长与L的关系为[3]
L=|nx|λnx=0,±1,±2,±3,…
而其波矢的可能值为
由德布罗意关系可知,一维光子的动量的可能值为
一维光子的能量的可能值为
对于三维情况,粒子的三个动量分量的可能值为
在p+dp范围内,动量的三个分量的可能状态数为
在体积V=L3内,平衡辐射的量子态数可能值为
我们用动量的球坐标求出平衡辐射的可能状态数为
由于光子有±h两个可能的值,上式应乘以2。
2.2 平衡辐射的普朗克公式
光子的自旋量子数为1,光子是玻色子,平衡时满足玻色分布,且其化学势为0,根据化学势与α的关系为:
可知:α=0
这样平衡辐射的玻色分布为
所以每个状态的平均光子数为
光子气体符合德布罗意关系
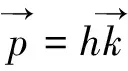
ε=hω
由于圆频率与波矢k存在以下关系
ω=ck
可知:ε=cp

因此,辐射场的内能为
(4)
这就是著名的普朗克公式,与实验结果完全相符。
3 普朗克公式的重要推论

(5)
这就是瑞利-金斯公式。
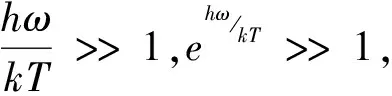
(6)
这就是维恩公式。
3)对普朗克公式积分,可求得空间辐射的内能

积分得
(7)
这就是斯特藩-玻耳兹曼定律。
4)维恩位移定律
利用上式可得辐射场圆频率的极大值,即
可得 3-3e-x=x

ωm≈2.822kT/h
此结论说明,圆频率的极大值与温度成正比,这个结论称为维恩位移定律。
4 结语
普朗克的量子统计理论彻底摒弃了经典理论的缺陷,把量子统计物理提高到一个崭新的阶段。其对平衡辐射的高频段和低频率段的研究运用,取得了与实践完全一致的结果,并科学地把瑞利-金斯公式和维恩公式结合在一起。利用普朗克的量子统计理论还可以推导出很多其他的重要结论,这一理论对量子统计物理学的创建起到极为重要的作用。
[参考文献]
[1] 林宗涵.热力学与统计物理学[M].北京:北京大学出版社,2007:282-284.
[2] 崔海宁.热力学系统理论[M].长春:吉林大学出版社,2009:140-142.
[3] 李鸿寅.热力学及统计物理[M].郑州:河南大学出版社,1988:250-254.
——莫里斯·威尔金斯

