广义生物经济模型的控制
佟 欣
(大庆师范学院 数学科学学院,黑龙江 大庆 163712)
0 引言
物种的增长都有一个完整的成长发育过程, 在发育过程中物种在各个生命阶段的出生率、 死亡率、 扩散率、 捕食能力等有着明显差别,这些因素都在不同程度上影响着生物种群的持续生存和灭绝,因此, 我们建立了具有阶段结构的种群模型[1-5]。阶段结构的种群模型可以用微分方程组表示为:
(1)

1 模型建立
如果人类对模型(1)中的成年种群进行捕获,研究人类的经济活动和捕获行为对生物种群发展动态的影响,从而建立广义生物经济模型如下:
(2)
其中x1(t)、x2(t)、a、α、b、β的含义同式(1),E(t) 表示t时刻对成年种群的捕获量,p为单位成年种群价格,c为捕获成本,m为经济利利润(剩余量) ,p、c均为大于零的常数, 所以pE(t)x2(t)表示收益总量,cE(t)表示总成本。方程(2a) 、(2b) 分别表示幼年种群和成年种群的增长率, 方程(2c) 表示收益总量, 总成本以及经济利润(或剩余量) 之间的关系。 显然,模型(2)是一个微分代数系统,x1(t) ,x2(t)是微分变量,E(t)是代数变量。
2 模型研究
2.1 奇异诱导分岔
当建立的广义生物经济模型(2)中的经济利润为零时,即m=0时,会出现 Cordon所提出的生物经济平衡现象,也称为“ 经济学过度捕捞”[1]现象,就是说经济利润被捕获的强弱程度即努力量所制约着[2],两者之间处于水平消耗的关系,收益和成本就可能相等,所以可以得出模型(2)存在平衡点:
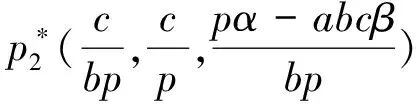
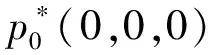
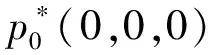
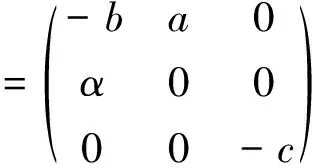

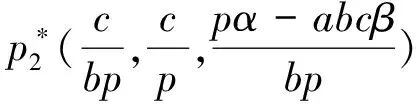
2.2 奇异诱导分岔的状态反馈控制
综合上述分析可知:当分岔值m=0时,即经济利润为零时,广义生物经济模型(2)的克罗内克(kronecker)指标将增加,从而导致系统出现奇异诱导分岔现象。为了消除这种分岔现象,我们需要在模型(2)中施加控制系统使模型(2)中的克罗内克指标减少。
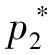
接下来我们确定一个可执行输入v(t)来分析受控模型情况。
(3)
(4)
得到模型
(5)
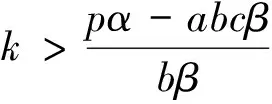
综上所述可以知道该状态反馈控制器的生物意义为:当我们对所捕获的努力量给予制约时,此时反馈增益K的值可以了解到,当增大捕获量时,就可以把经济系统的奇异又到分岔消除,就可以使得系统达到稳定状态。
3 数值仿真
为了说明状态反馈控制器的有效性,我们现将广义生物经济模型(2)中的各项参数取值,即a=4,b=8,α=4,其中b为幼年种群的死亡率和转化为成年种群的转化率之和,所以α (6) (7) 通过研究生态系统在受到外界因素干扰时,从而出现在广义生物经济模型中的奇异诱导分岔现象,并研究其在经济利润为零的条件下控制该现象的产生,设计状态控制器和研究该状态控制器的相关问题。当生物经济系统出现奇异诱导分岔现象时,会使种群数量在短时间内变化很大,即克罗内克指标发生变化。也就是说,经济利润为零时,当克罗内克指标增加1时,就会使得生物种群的数量超过环境可以承受的量,而此时生态环境就会发生变化。可以更好地解决奇异诱导分岔现象,从而使得种群达到平衡的状态,这样就会使得生态系统得到更好的保护。正因为如此,建立了反馈控制器,通过控制器捕获的努力量,来调整控制生态系统的相对平衡,从而达到保护生态资源和生态经济持续稳定发展的目的。最后根据所得到的真实数据说明了状态控制器的可行性。 [参考文献] [1] Clark C W. Mathematical Bioeconomics: The OptimalManagement of Renewable Resources[M].New York: Wiley,1990:27-72. [2] Yang L J,Tang Y. An improved version of thesingularity-induced bifurcation theorem [J].IEEE Transaction on Automatic Control, 2001,46(9):1483-1486. [3] 张悦.阶段结构广义生物经济模型的分岔及控制[J].系统工程学报,2007,22(3):233-238. [4] 陈兰荪.数学生态学模型与研究方法[M].北京:科学出版社,1988:199-231. [5] 马知恩.种群生态学数学建模与研究[M].合肥:安徽教育出版社,1996:330-364.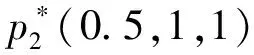
4 结语

