单层梁格分析宽翼缘箱梁剪力滞效应
戴树才,张 锋
(无锡市政设计研究院有限公司,江苏无锡 214072)
0 前言
伴随着我国交通事业的蓬勃发展,桥梁建设也得到了大力推进。然而桥梁病害却从未放弃困扰桥梁工程师们。如何建设精品工程是广大桥梁工程师所一直追求的。精心设计、精心施工是建设精品工程的必备条件。而设计是否可靠、实用、经济是依据工程计算分析结果来评判的。
桥梁结构计算方法,总体上可以分为两种:解析法和数值法。解析法通过基本条件的假定,通过数学、力学的方法来研究结构的受力,常用作理论分析。它的研究对象通常是规则的、理想的结构形式。而针对实际桥梁项目的设计验算,工程师常用借助计算机程序或软件,采用数值法来分析。可以对桥梁上部结构纵横向同时进行精细分析、可以采用影响面加载活载效应、可以采用较少的单元分析复杂的桥梁进行精确分析,梁格法已成为分析桥梁上部结构内力、变形的一种炙手可热的计算方法。
目前,广大工程师们所采用的主要是“Hambly”平面梁格法,该方法在实际运用中有许多方面还是值得改进的。
1 梁格法基本原理
从板式上部结构开始探讨,Hambly分析了梁板式、格构式、薄壁箱室等桥梁上部结构的力学性能,提出采用等效纵横梁格代替桥梁上部结构的方法来分析其内力、变形。结合已经发展成熟的6自由度空间杆系有限元理论,采用软件进行计算分析,梁格法大大提高了分析精度和工作效率。
2 “Hambly”平面梁格与单层梁格
梁格法应用的前处理主要有两大步骤:(1)离散桥梁上部结构用纵、横梁单元等效,即梁格划分;(2)纵、横梁单元截面刚度的赋值,即刚度取值。从以上两个方面入手,对平面梁格法作出改进,提出“单层梁格法”。
2.1 梁格划分
梁格法通过纵向梁格代表箱室纵向力学性能、横向梁格代表横向力学性能,来近似等效上部结构。因此,梁格法的计算精度与梁格划分关系非常密切,通常要求:(1)纵、横梁应与腹板位置重合,纵梁的划分应使得各纵梁的形心轴与整个截面形心轴重合,见图1、图2,等效梁格在同一面中,因此这里称其“平面梁格”;(2)纵横梁格长度比应为0.5~2,且应相互垂直或斜交较小;(3)在受力复杂或反弯点处宜适当加密网格;(4)离散后的梁格应与结构原受力特性保持一致。

图1 平面梁格划分
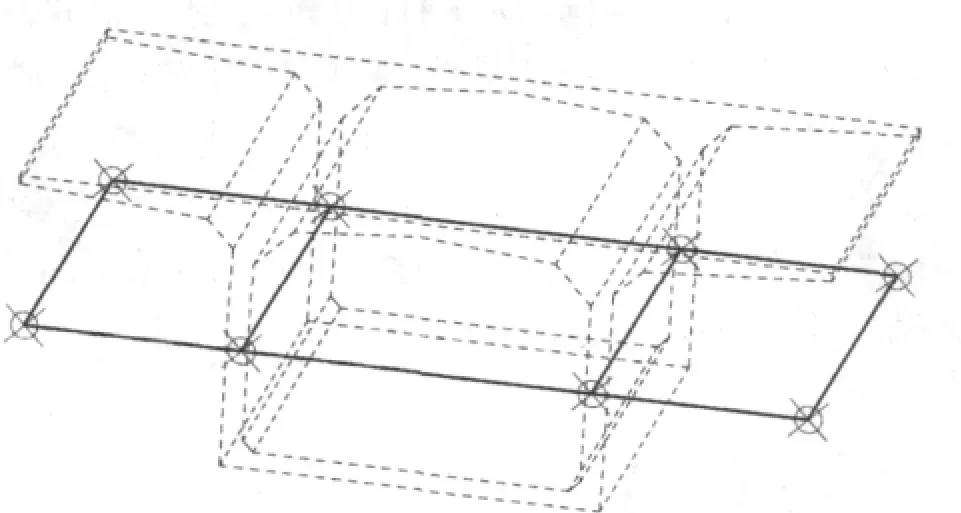
图2 等效平面梁格
遇到变腹板厚度箱室、斜腹板箱梁或者上部结构截面形式更复杂的时候,要满足(1)这个条件却是非常耗时和不经济的。我们认为这一点是可以改进的,纵梁的划分完全不用受到腹板的约束;在满足一些基本原则的情况下(如:截面剪力由腹板承担等),根据分析精度的需求,可以出现“一字梁”、“二字梁”加密梁格,见图 3、图 4。

图3 单层梁格划分

在广义的划分方法下,各个纵梁位置宜放置在各自的形心位置处,代表腹板的纵梁应与横梁作刚臂竖向链接(我们不采用梁格法来模拟箱室的框架受力特性)。这样离散后的梁格已不在一个面中,呈一层褶面,这里称其“单层梁格”。
2.2 刚度取值
在分析箱梁时,通常采用的“剪力柔性梁格”——平面梁格,在梁单元刚度值偏于复杂,单层梁格法做了一些简化工作。
(1)抗弯刚度
不要求划分后的纵梁形心轴与原截面相同,亦不要求各纵梁绕原截面形心轴计算抗弯刚度。各纵梁仅需绕各自形心轴计算抗弯刚度即可,需要注意的是“二字梁”是绕顶、底板组成的截面形心轴来计算的。有人担心,这样计算截面的抗弯刚度会减小,然而纵梁相对于弯曲中性轴的抗弯刚度为I=Iy+A×i2,这与平面梁格按照整个截面中性轴计算抗弯刚度的效果一致。

(2)抗扭刚度
在杆系软件里应用梁格法时,截面特性往往是采用软件自动生成的,但这是存在问题的。软件计算的抗扭刚度通常是该截面作为开口截面的抗扭刚度值,然而在箱梁里离散后的纵梁其实是闭合截面的一部分。这里推荐采用经验公式估算:

梁格计算所得的剪力流是不准确的粗糙的,即使将抗扭刚度调整得再精确也无济于事,因为切分梁格时很难找准剪力零点位置。
(3)剪切面积
剪力柔性梁格的特点就是修改剪切面积,使得在受剪力作用时,梁格的变形与实际的一致,见图6。然后,梁格法属于6自由度梁单元有限元方法,在梁单元里通常不计入剪切变形的影响,因为一般的桥梁上部结构不属于深梁,即使计入剪切变形,其计算结果也没有什么差异。因此,无需花费大量精力在修正剪切面积上,因为即使修正也无法使梁格法分析箱梁的畸变效应。
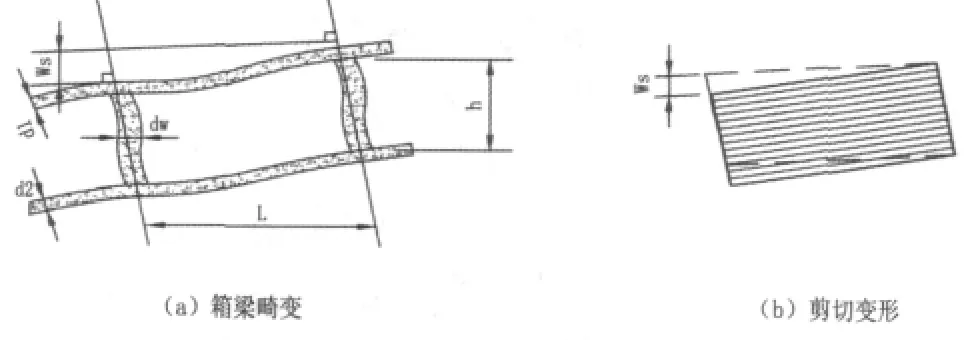
图6 箱形截面梁格的畸变
分析梁格模型时,应仅考虑腹板承受剪力,而“一字梁”、“二字梁”不承担剪力。
3 宽翼缘箱梁滞效应与分析方法
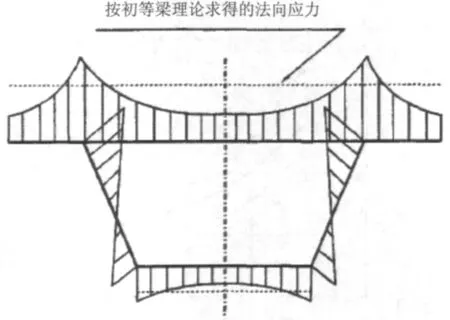
由于翼板的剪切变形沿宽度方向分布不均匀引起的,弯曲时远离腹板的翼板纵向位移滞后于近腹板的翼板纵向位移,所以弯曲正应力的横向分布呈现出曲线形状,这种由于翼板的剪切变形造成的弯曲正应力沿梁宽方向不均匀分布的现象称为“剪力滞效应”,见图7。剪力滞效应的大小通常采用剪力滞系数来表示,见式(2)。

精确分析剪力滞效应的方法有:(1)能量变分法;(2)比拟杆法;(3)数值分析法;(4)模型试验。当对实际工程进行计算分析时,通常采用有效分布宽度来估算。其中能量变分法从假定箱梁翼板的纵向位移模式出发,以沿梁长的竖向位移函数和翼板纵向位移差的广义位移函数为未知数,应用最小势能原理,建立控制微分方程,从而获得应力和挠度的闭合解。它很好地阐释了正、负剪力滞效应的产生与特性。
4 单层梁格法考虑剪力滞
不同于单梁模型,梁格模型对各纵梁截面内力进行了重分配,更逼近真实受力情况。梁格法的本质仍是一种近似模拟的方法,它无法得到考虑剪力滞影响后的光滑曲线,只能以阶梯状的形式表现出来,见图8。如果单元将单元划分得合理,那么它将能成功计算剪力滞效应,而且划分得越细,结果就越精确。那么宽翼缘的截面中,划分纵梁时其宽度W应该取多少合适呢?我们认为W应小于桥梁规范规定的无须进行有效分布宽度折减的宽跨比所对应的宽度。
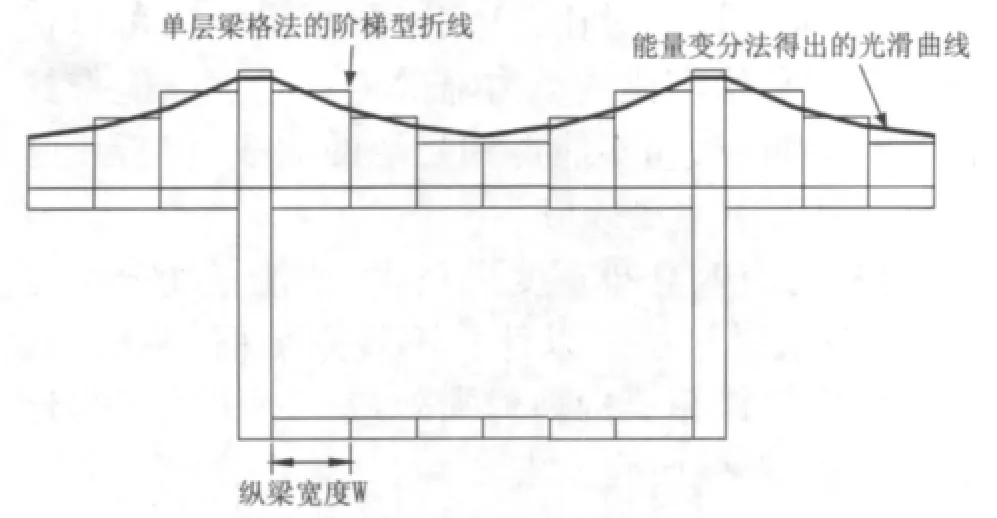
图8 考虑剪力滞的正应力曲线
选择规则矩形单箱单室截面[2](见图9,b=2.55,Is/I=0.767)的简支梁跨中受集中力作为计算对象,将单层梁格法的数值解与能量变分法的解析解作比较,验证其考虑剪力滞的正确性。单层梁格划分见图10。
不同跨宽比的简支梁在跨中集中力作用下,单层梁格法与能量变分法计算所得剪力滞系数对比见图11~图15。

图9 计算对象

图10 单层梁格划分(单位:m)

图11 L/2b=4时跨中截面剪力滞情况
从图11~图15中,可以看出:
(1)单箱室简支梁跨中受集中力作用下,跨中截面呈现正剪力滞效应,且该效应随着跨宽比增大而减小。
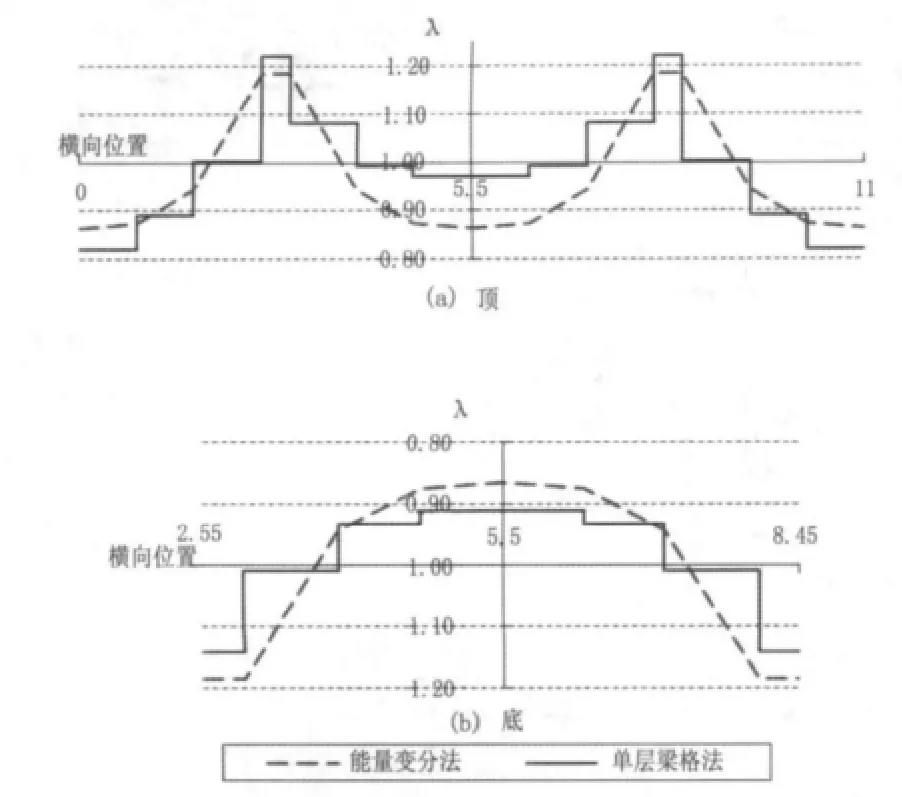
图12 L/2b=6时跨中截面剪力滞情况

图13 L/2b=8时跨中截面剪力滞情况

图14 L/2b=10时跨中截面剪力滞情况
(2)单层梁格法计算所得的跨中截面剪力滞效应与能量变分法趋势一致、数值相近。

图15 剪力滞效应随宽跨比变化而变化
(3)梁格计算所得顶底板剪力滞效应并不对称,表明了它的中性轴相对简单梁模型发生了变化。在单层梁格数值模拟计算时,是将集中力加载在腹板位置(与模型实验加载位置一致),这使得箱梁截面中性轴发生变化——箱体区域中心轴下降,翼板中性轴上升,换句话说各纵梁的竖向挠度并不完全相同;而能量变分法是采用规则的位移模式采用能量变分法计算剪力滞效应的,因此计算所得顶底板剪力滞效应是对称的。
5 结论
(1)本文对“Hambly”平面梁格的划分方法与刚度取值作出改进,提出了更符合实际运用、精细化分析的单层梁格法;同时明确了梁格法不能解决箱梁的畸变问题。
(2)通过计算对比,证实了单层梁格法可以正确计算宽翼缘箱梁的剪力滞效应;虽然只能得到阶梯形的折线,而不能得到光滑的曲线,但折线已足够表达其剪力滞效应。
(3)比有效分布宽度更精确、比能量变分法更实用,单层梁格法可以计算不规则截面、预应力、变高的宽翼缘箱梁的剪力滞效应,不失为工程计算的一种可靠、便捷方法。
[1]E.C.汉勃利.桥梁上部结构性能[M].北京:人民交通出版社,1982.
[2]张士铎.箱形薄壁梁剪力滞效应[M].北京:人民交通出版社,1998.
[3]E.C.Hambly.Bridge Deck Behaviour[M].London:E&FNSPON,1976.
[4]戴公连,李德建.桥梁结构空间分析设计方法与应用[M].北京:人民交通出版社,2001.
[5]王勖成,邵敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,1997.
[6]徐栋.桥梁体外预应力设计技术[M].北京:人民交通出版社,2008.
[7]郭金琼.箱形梁设计理论[M].北京:人民交通出版社,1991.

