容纳矛盾逻辑系统与悖论
张金成
(中央党校函授学院,安徽广德242200)
迄今为止,在数学的各个领域,已经建立了很多数学演绎系统,如自然数系统、欧氏几何系统、公理集合论系统、群论系统等.
罗素在《数学原理中》中给出的命题逻辑演算系统,是逻辑演绎系统.在命题逻辑演算的基础上,希尔伯特又建立了谓词演算系统,后来经过逻辑学家的简化、完善,形成了完整的逻辑演绎系统.演绎系统的本质特征是系统内部的无矛盾性,如果一个演绎系统可以得出矛盾,那么这个系统就会崩溃.经典逻辑认为矛盾即为错误,因此经典逻辑排除矛盾.在经典逻辑中若出现矛盾将导致整个体系“崩溃”,因为经典逻辑有一个“邓斯·司各特定律 A,¬A├B”,即矛盾将导致一切都成立,一切都不成立,因此该体系是无用的[1].
无矛盾的演绎逻辑系统已经发展得很完善,但由于悖论及处理矛盾的需要,近来又出现了容纳矛盾的逻辑系统.
1 矛盾的再研究
1.1 容纳矛盾的逻辑系统的现状
在数学领域中,人们逐渐意识到矛盾的不可排除性,自从20世纪60年代以来,一些逻辑学家开始研究在数学、逻辑中容纳矛盾,他们希望放弃一致性,或者兼容矛盾,因此产生了一门崭新的逻辑——容纳矛盾的逻辑.
目前有关容纳矛盾的逻辑的形式系统有很多,如美国逻辑学家R.Brandom的不协调逻辑、澳大利亚学者Priest的悖论逻辑、巴西逻辑学者Da Costa的次协调逻辑[2].
在对待矛盾的形式处理上,不同的逻辑也有不同的处理方式,他们都以小心谨慎的态度改造经典数理逻辑.但是为了容纳矛盾,其逻辑系统的人造成份太多,并不是对自然界和人类思维领域本身应有的矛盾规律的发现,他们所建立的形式系统还是探索性的、初步的和不成熟的.
笔者认为在数学、逻辑中容纳矛盾这种方案是正确的,只要建立起正确的形式系统,就可以建立一个容纳矛盾的数学基础.无论是不协调逻辑、超协调逻辑,还是次协调逻辑,这些逻辑系统仅仅能容纳矛盾,不能彻底解决矛盾,这是因为这些逻辑系统在矛盾的本质规律的形式表述上是不精确的.本文在对欧氏几何与非欧几何的矛盾进行研究的基础上,提出一个容纳矛盾的新系统S.
1.2 相互矛盾的系统
19世纪初,俄罗斯数学家罗巴切夫斯基在试图证明欧氏几何的第5公理(平行公理)时,发现了“平行公理”既不能被证明,也不能被否证,欧氏几何平行公理是独立的,从而发现了一种全新的几何——非欧几何(罗氏几何).后来,德国数学家黎曼又发现了另一种非欧几何——黎氏几何.
非欧几何与欧氏几何相比,具有如下特点:
1)欧氏几何与非欧几何有几条公理是相同的;
2)欧氏几何与非欧几何有1条公理是相矛盾的;
3)欧氏几何与非欧几何内部是相对一致的,但是欧氏几何与非欧几何之间是相矛盾的;
4)欧氏几何与非欧几何是相互翻译的,即欧氏几何与非欧几何是同构的.
类似于非欧几何产生的例子,在科学界还有很多,具有一般的规律性,这种思维方式很值得研究,本文试图把这种思维方式一般化,抽象出一般的思维公理,模拟其思维过程,建立一个新的逻辑系统.
人们知道,欧氏几何由5组公理组成:结合公理Ⅰ1-8、顺序公理 Ⅱ1-4、合同公理 Ⅲ1-5、连续公理Ⅳ1-2和平行公理Ⅴ.其中Ⅰ ~Ⅳ称为绝对几何公理体系,记为绝对几何公理体系∏ ={Ⅰ,Ⅱ,Ⅲ,Ⅳ}.平行公理有以下3种:
1)欧氏平行公理Ⅴ:过已知直线外一点,只能作惟一一条直线与已知直线平行.
2)罗氏平行公理¬Ⅴ:过直线外一点,至少可以作2条直线与已知直线平行.
3)黎氏平行公理¬Ⅴ:过直线外一点,不可以作直线与已知直线平行.
以上3种相互矛盾的平行公理与绝对几何公理体系结合,可以产生3种相互矛盾的几何,即欧氏几何、罗氏几何和黎氏几何.用¬Ⅴ表示平行公理的否定命题,在绝对几何公理体系中,∏├/Ⅴ,且∏├/¬Ⅴ,Ⅴ在∏中是不可判定命题,即第5公理在绝对几何体系中是独立的[3].
欧氏几何与非欧几何可以分别表示为∏∪{Ⅴ}={I,Ⅱ,Ⅲ,Ⅳ,Ⅴ}欧氏几何公理体系、∏∪{¬Ⅴ}={Ⅰ,Ⅱ,Ⅲ,Ⅳ,¬Ⅴ}非欧几何公理体系.欧氏几何公理体系∏∪{Ⅴ}={Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ}的内部是相容的,非欧几何公理体系∏∪{¬Ⅴ}={Ⅰ,Ⅱ,Ⅲ,Ⅳ,¬Ⅴ}的内部也是相容的.但是∏∪{Ⅴ}与∏∪{¬Ⅴ}是矛盾的,所以∏∪{Ⅴ}与∏∪{¬Ⅴ}不能合并在一起,它们分别处于2个不同的领域,即欧氏几何领域与非欧几何领域.从这里可以看到,矛盾可以在不同的领域成立.
欧氏几何学、罗氏几何学、黎曼几何学是3种互有区别的几何学,这3种几何学各自所有的命题都构成了一个严密的公理体系,各公理之间满足一致性、完备性和独立性,因此这3种几何学都是正确的.
从罗巴切夫斯基、黎曼创立的非欧几何学中,可以得出一个极为重要的、具有普遍意义的结论:逻辑上互相不矛盾的一组假设都有可能提供一种新的理论.
一般地,用A表示矛盾的正命题,¬A表示矛盾的反命题,以上A与¬A是一种相互矛盾的否定方式,但它们能在不同的条件下成立,这种可以在不同条件下成立的思维方式,称它为辩证矛盾思维.它正是非欧几何产生的思维方式,其本质是研究不同领域中相互否定的命题的表示和逻辑规律.
1.3 正域、反域与不动域
把一个原命题成立的领域叫做正域,而把相对于正域之外的其否定命题成立的领域叫做反域.
例1 正数领域、实数领域、欧氏几何领域叫做正域,则负数领域、虚数领域、非欧几何领域叫做反域.
正域与反域是什么关系?正数领域与负数领域可以一一对应;实数领域和虚数领域也可以一一对应;欧氏几何领域和非欧几何领域可以相互翻译等等.通过分析可知,一般现实情况下,正域与反域是一种此消彼长的不等价关系,这是因为矛盾的双方发展不均衡,某一方处于缺损状态;但在理想状况下,正域与反域之间的关系是:性质相反,一一对应的两个同构世界.
很多正域与反域是一种等价的均衡关系,数学理论上、物理理论上的矛盾域多是等价的.因此,讨论正域与反域上等价的逻辑关系具有重要意义.
定义1 若有一个正世界个体域+α={t1,t2,…,tn},通过某种反变关系f,所得到一个新的反变世界个体域 -α ={f(t1),f(t2),…,f(tn)},且ti≠f(ti),在+α中的元素都具有性质P,即命题P(t)成立;在 -α中的元素都具有性质¬P,即命题¬P[f(t)]成立.把+α叫做正域,-α叫做反域,反域也记为 - α =1,2,…,n}.
在定义1中,+α与-α是对等关系(均衡的、同构的或可翻译的).
在以上概念的基础上,把矛盾命题重新进行形式化描述如下.
1)A:在欧氏几何领域,过已知直线外一点,只能作惟一一条直线与已知直线平行,形式描述为A+α.
2)非A:在非欧几何领域,过已知直线外一点,并非只能作惟一一条直线与已知直线平行,形式描述为¬A-α.
A+α表示正域+α中的命题A,A-α表示反域-α中的命题A,即在非欧几何领域,过已知直线外一点,只能作惟一一条直线与已知直线平行.¬A-α表示反域-α中的命题¬A,¬A+α表示正域+α中的命题¬A,即在欧氏几何领域,过已知直线外一点,并非只能作惟一一条直线与已知直线平行.这样,矛盾命题都有2种表示方式.
定义2 在相同域上的否定命题Aα与¬Aα(即A+α与¬A+α或 A-α与¬A-α),称之为经典矛盾命题;在不同域上的否定命题(A+α与¬A-α或 A-α与¬A+α),称之为非经典矛盾命题或辩证矛盾.
实际上,矛盾命题在不同域上成立,矛盾也就被化解了,辩证矛盾就是已经被化解或者解释清晰后的矛盾.
由于公式的变化,公理在不同域中有些变化,经典逻辑公理[4]在正域中变为:

经典逻辑公理在反域中对应变为:
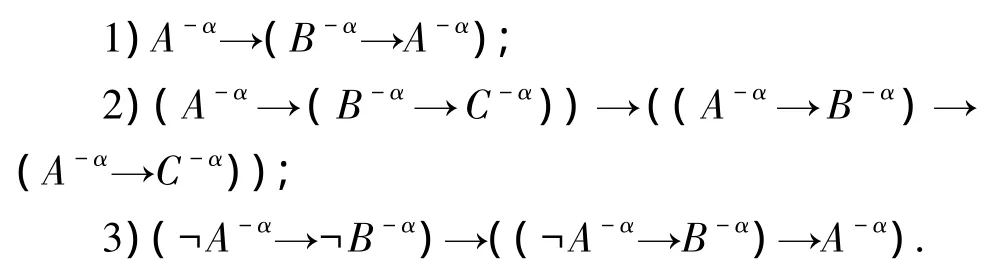
由于经典逻辑的公理在正域和反域上都是成立的,因此对正反2个域上都成立的命题,不再用上标+α、-α来区分这2个域,而上标只标为α,或者与经典逻辑公式一样不标.如 Aα→(Bα→Aα)和A→(B→A)在正反2个域上都成立,这2个表示的是一个意思.
正域和反域往往不是对立的,它们中间还可能有一个既具备正域性质又具备反域性质的中间域,如正数和负数中间有中间数0.
在正域和反域中,若存在某些个体k1,k2,…,kn,通过某种反变关系 f,有 f(ki)=ki,则把个体 k1,k2,…,kn所形成的集合叫做关于映射f的不动域,记为 +e={k1,k2,…,kn},-e={f(k1),f(k2),…,f(kn)}.由于 f(k1)=k1,f(k2)=k2,…,f(kn)=kn,所以 +e={k1,k2,…,kn}={f(k1),f(k2),…,f(kn)}=-e.
定义3 对于一个正域+α={t1,t2,…,tn}与反域 -α ={f(t1),f(t2),…,f(tn)}上的反变关系 f,若存在某些个体 k1,k2,…,kn,通过反变关系 f,有f(ki)=ki,则把个体 k1,k2,…,kn所形成的集合叫做关于映射f的不动域,统一记为
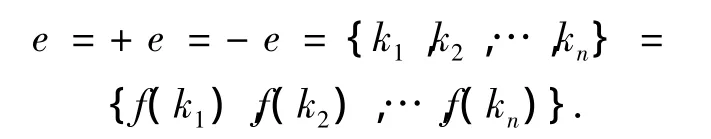
例2 若f(x)=-x,则正数领域、负数领域关于映射f(x)=-x的不动域是e={0}.
Aα是集合 α 上的命题,A+α、A-α、Ae分别是正域命题、反域命题和不动域命题.
不动域是从正域到反域的映射过程中保持原地不变的所有个体形成的集合,不动域既具备正域性质,又具备反域性质.在不动域中P(k)与¬P[f(k)]相互否定,即自身与自身相互否定.不动域与不动点相类似,函数的不动点,在数学中是指被这个函数映射到其自身的一个点.设f是从x到x的一个映射或运动,把每一点x移到点f(x).方程f(x)=x的解恰好就是在f这个运动下被留在原地不动的点,故称不动点.不动点就是自指代方程的解[5].
例3 设在平面上给定一个以O为中心,R为半径的圆C,P是平面上异于点O的任一点,在射线OP上,考虑其中一点P'满足OP·OP'=R2,称P'为P的反演点,将点P变到点P'的过程称为反演变换.反演变换是一个关于圆的对称变换,容易证明,圆外的每一点P'通过变换对应于圆内的每一点P,圆心O对应于平面上无穷远点,圆上的点对应它自己,即圆上的点是关于反演变换的不动点.
因此,正域与反域是关于某个映射f的对称变换,+α中的项t对应-α中的项,不动域中的项对应它自己.
1.4 正反域对偶变换公理
下面将进一步研究跨域的命题之间的关系,即正命题P+α与反命题¬P-α之间是什么关系?
首先考虑欧氏几何与非欧几何之间的关系,在证明非欧几何(以罗氏几何为例)的相容性时,使用了一种单位圆的内部的线性变换,即非欧几何的庞加莱模型.有了由一个圆代表的非欧平面和非欧变换,那么以此可建立非欧点、非欧直线、非欧角、非欧距离、非欧圆、非欧三角形等非欧概念,并建立相关的非欧命题.每一个非欧几何的概念、命题都可以变换(翻译)成欧氏几何的概念和命题,反之也成立.
通过大量例子,可以发现 P+α与¬P-α是等价的,如欧氏几何与罗氏几何是同构的,它说明一个命题等价于它反域中的否定命题,即应有公理P+α↔¬P-α成立.
定义4 正域+α、反域-α、不动域e集合的并集U,即U=+α∪e∪-α,称之为全域.
设命题P是关于正域+α、反域-α的一个划分,若 P=+ α,则¬P=- α,f:U→U,ti∈ + α,i∈- α,i=f(ti),有 P(t)↔¬P().
根据以上分析,可以引进一条新公理:P+α↔¬P-α.
定义5 称公理P+α↔¬P-α为正反域对偶变换公理.
1.5 悖论是逻辑思维领域的“不动点”
为了弄清悖论的机理,还是从分析一个函数自指代方程的不动点开始.

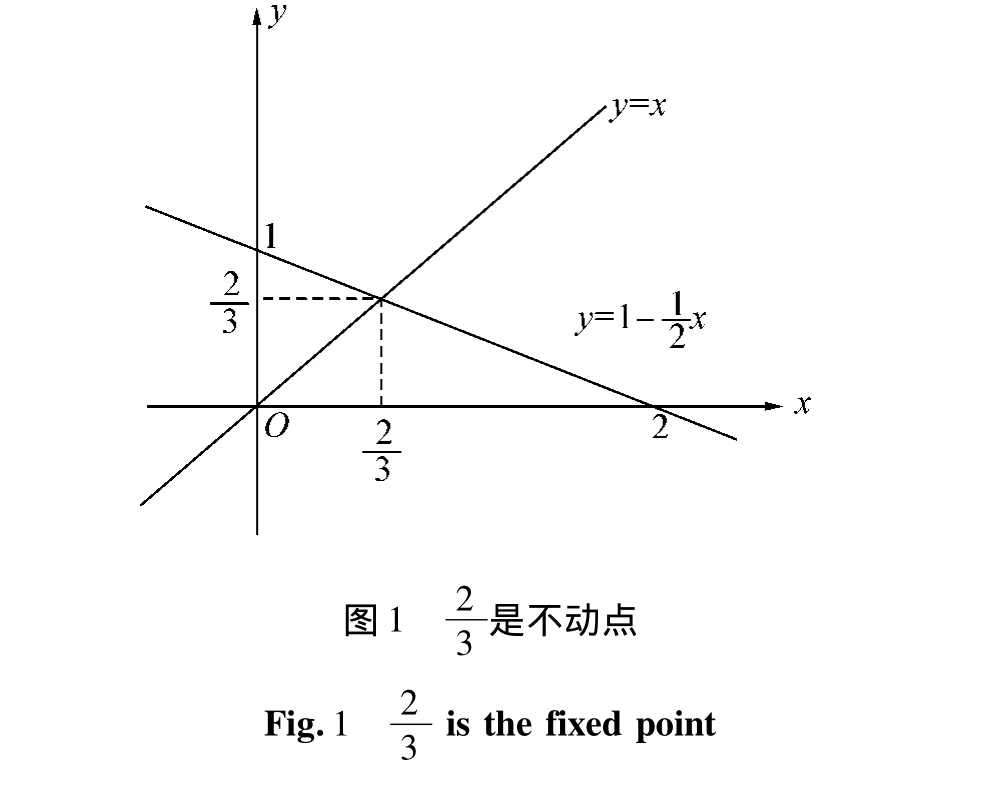
一般地,函数y=f(x),如果用x取代y,得函数方程x=f(x),则把x=f(x)叫做y=f(x)的自指代方程.如果方程x=f(x)有解x0,那么x0就是自指代方程的不动点.
点x0把实数集合分成2个性质相反的集合,其中一个集合中的元素满足性质P,另一个集合中的元素满足性质¬P,而不动点x0可以看成具有2个矛盾性质P与¬P的点,这就是悖论形成的内在机理.
关于函数不动点有“Brouwer不动点定理”:设f∶[0,1]→[0,1]是连续映射,则必存在 x0∈[0,1],使f(x0)=x0.这是一维的Brouwer不动点定理,不动点定理可以推广到二维以及n维欧氏空间中(即平面上的单位闭圆盘B2具有不动点性质,即任一连续映射f:B2→B2具有不动点).
不动点的性质已经不仅仅局限于代数和函数领域,它已经延伸到集合论、离散数学和计算机等其他各个领域[6].
下面看“罗素悖论”.集合分为2类:1)自身是自身的元素,看成是正域.即+α={x|x∈x};2)自身不是自身的元素,看成是反域.即-α={x|¬(x∈x)}.现在构造第2类集合全体组成的集合R,即x∈R↔¬(x∈x),问集合R是哪类集合?即用R去自指代.无论集合R是哪类集合,即能得到罗素悖论:R∈R↔¬(R∈R)[7].
在正域与反域之间存在一个不动域e={x|(x∈x)∧¬(x∈x)},它既有正域性质,又有反域性质.罗素集合 R={x∶x∉x},是满足 R∈R↔¬(R∈R)的解,是正域与反域的不动点.次协调逻辑的创始者Da Costa与Arruda已经初步建立了正反域集合理论,并研究了罗素集合的一些性质.同样,逻辑思维领域也存在不动点,无论什么悖论,它们都是“正反域对偶变换公理P+α↔¬P-α”在不动域e上的特殊表现形式.
2 容纳矛盾系统S与悖论定理
2.1 容纳矛盾的新系统
在以上一阶语言的基本符号、形成规则和定义下,引入上述公理和基本符号,可以在经典命题演算逻辑[1]的基础上建立如下系统.
1)命题演算公理.
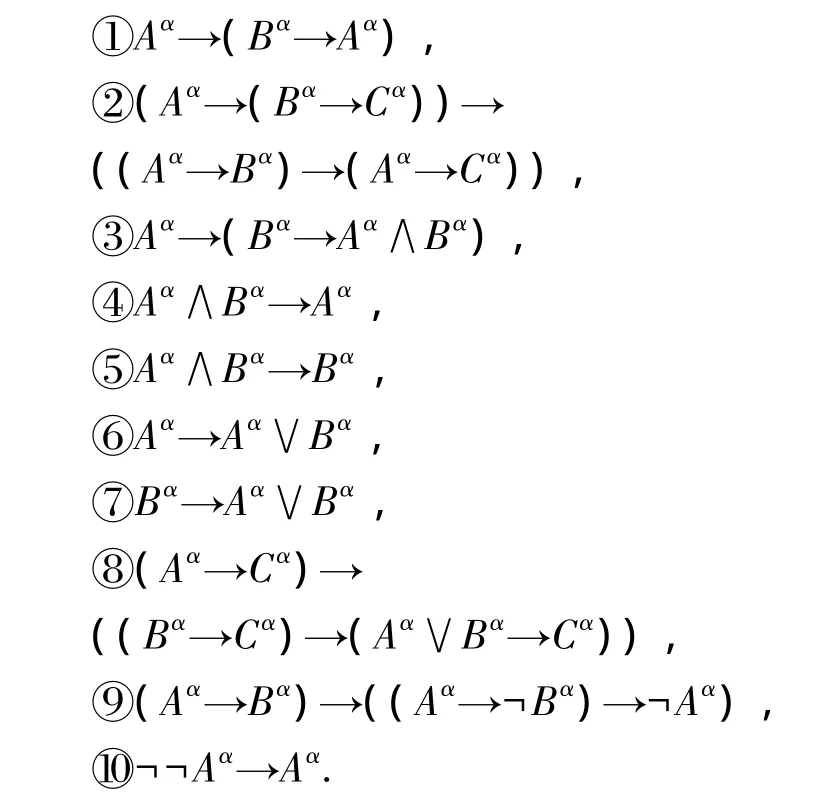
2)正反域对偶变换公理:P+α↔¬P-α.
3)演绎推理规则.分离规则:若├Aα,且├Aα→Bα,则├Bα.
定义6 由上述命题演算公理、正反域对偶变换公理和演绎推理规则3个部分组成的系统,叫做容纳矛盾系统S.
在系统S中,其中,α可以是+α,也可以是-α、e或U;并且在同一域中,它们都是经典定理.其实α是+α、-α、e、U时,所有的变元都成立,这种所有变元都成立的公式就是经典公式,以后可以省略其上标α.
2.2 相同域中的命题演算定理
由于容纳矛盾系统S是经典逻辑的扩展,所以所有经典逻辑的定理与演算模式在系统S中都是有效的.
定理1 在相同的域中,经典定理逻辑的所有定理都成立,如:
1)同一律:Aα→Aα;
2)排中律:Aα∨¬Aα;
3)不矛盾律:¬(Aα∧¬Aα);
4)双否律:¬¬Aα↔Aα.
定理2 Aα,¬Aα├Bα,即经典邓斯·司各特定律仍然成立.
以上定理说明,经典矛盾可以得出一切公式都是定理,仍然导致系统整个演算崩溃.
2.3 跨越正域与反域之间的命题演算定理
由于P+α、P-α是跨越了2个不同的领域,利用2个不同领域的变换,可以得到跨越了2个不同领域的一些新的演变定理.
定理 3 ¬P+α↔P-α.
定理3是正反域对偶变换公理的另一种形式,说明了一个命题等价于它反域中的否定命题.例如“三角形内角和等于180°”等价于反域中“三角形内角和不等于180°”.
定理 4 ¬(P+α↔P-α).
定理4说明了同一个命题在2个不同领域中不是等价的.例如“实数域中,数的平方大于零(非零数)”与“虚数域中,数的平方大于零”不等价.
定理 5 P+α∨P-α.
定理5说明了同一个命题必然在一个领域中成立.例如“实数域中,数的平方大于零(非零数)”和“虚数域中,数的平方大于零”必然成立.
定理 6 ¬(P+α∧P-α).
定理6说明了同一个命题必然在2个不同领域中不能同时成立.例如“欧氏几何领域中,三角形内角和是平角”和“非欧几何领域中,三角形内角和是平角”不能同时成立.
定理7 在系统 S 中,¬(P+α∧¬P-α),P+α∧¬P-α都不是定理(这在以下的语义模型中可以得到检验),即辩证矛盾不必然是定理.
定理 8 如果├P+α,则├P+α∧¬P-α,即 P+α和¬P-α可以同时成立,即辩证矛盾可以同时成立.
由于系统S是一个处理矛盾的系统,它也可以被看成是一个容纳矛盾的系统.在系统S中,有一些公式是不可证的(见定理9~10),这在以后的语义模型中可以得到证明.
定理9 在系统S中,
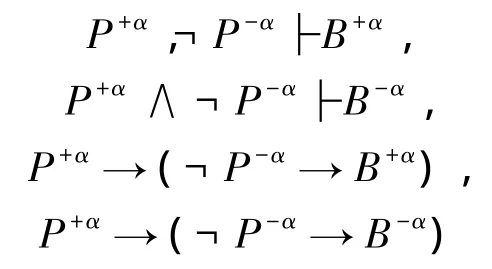
都不是定理.
以上定理说明,非经典矛盾P+α∧¬P-α不会得出一切公式,因此不会导致整个演算崩溃.
定理 10 在系统 S 中,¬(P+α∧¬P-α)与P+α∧¬P-α都不是定理.
这在以后的语义模型中可以得到检验,即非经典矛盾不必然是定理.
2.4 “悖论定理”与不动域中的命题演算定理
定理11(悖论定理)Pe↔¬Pe.
证明 由正反域对偶变换公理可以知道,在正域与反域中,P+α↔¬P-α;在不动域中,P+e↔¬P-e;在不动域中,+e=-e=e,Pe↔¬Pe.所以 Pe是关于正反域上Pe↔¬Pe的不动命题,正反域上的不动命题就是悖论,不动域命题是逻辑思维领域的不动点(笔者以后将证明“罗素悖论”也是集合论领域的一个不动点).因此可以看出“悖论”在系统S中不再是被排除的怪物,它是系统的一个定理.
定理12 在不动域中,命题¬Pe→(Pe→Be)、Pe∧¬Pe、Pe∧¬Pe→Be、Be都是定理.
由以上不动域的定理可以看出,不动域e是一个悖论性的域,其中的命题既真又假,其中任何命题都成立,任何命题又都不成立.在这个悖论性域中不能建立命题演算,经典逻辑演算在其中塌缩为一个逻辑命题,即Be.命题演算在不动域e中的崩溃,并不影响整个逻辑系统在正反域上的有效.我们并不能证明Bα是定理,因此整个逻辑系统是成功的.
Da Costa的次协调系统Cn没有严格区分矛盾,矛盾仍然用A∧¬A表示,该系统与经典逻辑相冲突.系统S把矛盾放在不同域上区分为经典矛盾和非经典矛盾,系统是经典系统的扩展,不与经典逻辑相冲突.
Da Costa的次协调系统Cn使经典逻辑的邓斯·司各特定律Aα,¬Aα├Bα失效,但且没有科学的依据.系统S中邓斯·司各特定律并没有失效,但是非经典矛盾下“P+α,¬P-α├B+α”是失效的[2].
Da Costa的次协调系统Cn虽然可以容纳矛盾,但是并没有把矛盾解释清晰.系统S表明P∧¬P可以为真,实际上是矛盾的双方在不同域中可以为真或不动域命题可以为真,即 P+α∧¬P-α和 Pe∧¬Pe可以为真.
系统S与经典系统的对比及修正如表1,其中,正域与反域之间通过公理P+α↔¬P-α可以转换,辩证矛盾命题成立.

表1 各个域上命题演算的对比Table 1 The comparison of propositional calculus on each field
3 容纳矛盾系统S的语义模型
3.1 语义解释
定义7 容纳矛盾系统S的模型是一个有序二元组(α,V),记为 M=(α,V),α 是正反世界上的个体域,V称为以α为个体域的赋值,它满足以下3个条件的函数:
1)对于系统中的每一个t,都有V(t)∈α;
2)对于系统中的一个n元谓词An(n=1,2,…)都有V(An)⊆αn,即V(An)是α×α×…×α的一个子集,是α上的一个n元关系;
3)正域 + α ={t1,t2,…,tn},反域 - α ={1,2,…,n},即正域与反域是对等的,U=+ α∪e∪ - α.
命题集合2α={A|A⊂α},A∈2α是 α 的子集合.Aα是集合α上的命题,α是域的变元,只可能是+α、-α、e、U 4种.
定义8 容纳矛盾系统S的模型为M=(α,V),其中赋值V满足S中公式A的递归定义:
2)如果A是公式B→C,V(B→C)=1当且仅当V(B)=0或 V(C)=1;V(B→C)=0当且仅当V(B)=1且V(C)=0;
3)如果A是公式B∧C,V(B∧C)=1当且仅当V(B)=1且 V(C)=1;V(B∧C)=0当且仅当V(B)=0或V(C)=0;
4)如果A是公式B∨C,V(B∨C)=1当且仅当V(B)=1或 V(C)=1;V(B∨C)=0当且仅当V(B)=0且V(C)=0;
5)如果 A是公式¬B,V(¬B)=1当且仅当V(B)=0;V(¬B)=0当且仅当V(B)=1;
6)如果 A是公式 P+α或 P-α(P 是 +α、-α 的一个划分),V(P+α)=1 当且仅当V(P-α)=0;V(P-α)=1 当且仅当 V(P+α)=0;
7)如果 A是公式 Pe,V(Pe)=1当且仅当V(Pe)=0,Pe是正反域上的不动命题.
定义9 容纳矛盾系统S中,若在单一的域α中,Aα在模型M=(α,V)中,恒有 V(Aα)=1,即 M⊧Aα,则公式Aα称作系统S的有效公式,即为永真公式[8].
3.2 元定理
依据以上解释,可以证明容纳矛盾系统S的元定理.
引理1 容纳矛盾系统S中的全部公式可以翻译成经典命题演算系统的公式,即系统S与经典命题演算系统等价.
证明 容纳矛盾系统S中的任意公式,如果只在一个域中,即只含有单一的+α,则记为F(+α),或含有单一的-α,则记为F(-α),这种在一个域中的公式就可以被认为是经典公式,统一记它为F(α).如果系统S中的任意公式跨越正反2个域,则统一记它为F(+α,-α).根据公理P+α↔¬P-α可以得到P-α↔¬P+α,任一个含有-α反域的公式可以替换成正域命题演算公式.因此,系统S中跨越正反2个域的公式F(+α,-α),一定可以转化成只含有单一+α的F(+α),或只含有单一-α的F(-α),即系统S中的任意公式可以转化成经典命题演算公式F(α).所以,容纳矛盾系统S与经典命题演算系统等价.
由于容纳矛盾系统S与经典命题演算系统等价,所以经典逻辑的元定理在系统S中仍然成立,根据引理1可以很容易证明以下的定理13~18.证明方法与经典逻辑系统方法相同[9-10],这里不再给出.
定理13(可靠性定理) 若 S├Aα,则 M0⊧Aα或 V(Aα)=1.
定理14(一致性定理) 在+α与-α中,不存在公式 Aα,使得├Aα和├¬Aα同时成立.
定理15(句法可判定性定理) 存在一般程序,判定一公式是否为容纳矛盾系统S的定理.
定理16(语义可判定性定理) 存在一般程序,判定一公式是否为容纳矛盾系统S的有效公式.
定理17(完全性定理) 在容纳矛盾系统S中,若 M0⊧Aα或 V(Aα)=1,则 I0├Aα.
定理18(不一致性定理) 在不动域e中,存在公式Pe,使得├Pe和├¬Pe同时成立.
4 结论
现行的所有数学分支基本上都可以建立在集合论的基础上,但是,自从集合论发现了悖论以后,围绕着数学基础的争论产生了三大学派——形式主义、逻辑主义和直觉主义.无论哪个学派,关于数学基础的最终意义目前还没有解决.
什么是数学基础?笔者认为数学基础就是全部数学的管理体制,当然它也是数学的一部分.这个管理机构有多个层次,最基本的应该是逻辑系统,次一级的是各个具体领域中的数学公理系统,数学公理系统只在具体某个数学领域中起作用,而逻辑系统无论在哪个层次都是通用的.
为什么要建立数学基础?不建立数学基础不行吗?笔者认为建立数学基础的原因是数学中出现了悖论、矛盾等.为了在数学中化解矛盾,就必须建立数学基础,它是数学发展到一定阶段的必然产物.就像人类社会的国家政府机构的建立一样,是矛盾发展到不可调和的产物.
由于矛盾命题在不同领域中都可以为真,所以在容纳矛盾系统S中,任何数学真理都只是在一定的条件下是真理,超出一定的条件它就成了谬误.任意命题A本身并没有真假,或者既可能是真也可能是假,当它相对于自身的域都是真的,相对于非自身的域都是假的.因此,数学真理都是相对的,只有在一个相对于自身的领域,数学真理才具有绝对性.
[1]S.C.克林.元数学导论[M].莫绍揆,译.北京:科学出版社,1984.
[2]桂起权.次协调逻辑与人工智能[M].武汉:武汉大学出版社,2002.
[3]傅章秀.几何基础[M].北京:北京师范大学出版社,1984.
[4]HAMILTON A G.Logic for mathematicians[M].Cambridge,UK:Cambridge University Press,1978.
[5]江泽涵.不动点类理论[M].北京:科学出版社,2011.
[6]张奠宙,顾鹤荣.不动点定理[M].沈阳:辽宁教育出版社,1995.
[7]汪芳庭.数学基础[M].北京:科学出版社,2001.
[8]何华灿.泛逻辑学原理[M].北京:科学出版社,2001.
[9]桂起权,陈晓平.辩证逻辑形式化的研究纲领[J].云南社会科学,1992(5):43-49.
[10]胡世华,陆钟万.数理逻辑基础[M].北京:科学出版社,1981.

