概率联系数化的原理及其在概率推理中的应用

赵森烽，赵克勤

(1.浙江工业大学之江学院 理学系，浙江杭州 310024;2.诸暨市联系数学研究所，浙江 诸暨 311811;3.浙江大学非传统安全与和平发展研究中心，浙江杭州 310058)

不确定性是人工智能面临的挑战之一［1］.目前处理不确定性的成熟的数学理论是概率论，而概率是概率论的基石［2］.

集对分析(set pair analysis，SPA)是一种新的处理不确定性的系统数学理论，已得到广泛应用［3-13］，联系数是其中的基本数学工具.文献［14］最早指出集对分析与概率论的联系和区别，主要区别在于:概率论侧重于从“不确定性可以在一定条件下(例如让随机试验次数n→∞)加以确定”这一角度来描述和分析随机不确定性，而SPA同时从“不确定性可以在一定条件下加以确定”以及“不确定性的本质是不确定的，必须加以客观承认”这2个方面来描述和分析不确定性.文献［5］又指出经典概率统计理论中的概率仅与联系数中的同一度等价.文献［15］指出了概率联系数化的可行性和必要性，可行性是指概率P是一个在［0，1］取值的实数，因而可以联系数化成P+(1－P)i;另一方面，把概率P联系数化成联系数P+(1－P)i也是必要的，因为概率是从宏观层次上对随机不确定性的数学描述，所以显示出随机不确定性的确定性;但在微观层次上，随机不确定性其本质是不确定的，因此，当需要同时从宏观与微观2个层次上考虑随机不确定性的程度、作用和影响时，把概率P联系数化成P+(1－P)i就显得完全必要.此外文献［15］还指出，把概率用联系数的形式表示在理论和实践上都有重要的意义.

本文在上述工作的基础上进一步用实验阐明概率联系数化的原理，定义随机试验中具有随机性的事件为随机事件，借助实验说明事件的随机性来自事物与事物的联系，随机事件因此成对存在.但可以根据某种准则(例如关注程度、出现的先后、参考事件的设定等)分为主事件和伴随事件，由此又导出主概率和伴随概率，它们分别对应于主事件发生的大数概率(随机试验中次数频率稳定性的概率)和主事件的即或概率(随机试验中主事件不发生但伴随事件发生的概率).用联系数表示主事件的大数概率和主事件的即或概率，称此联系数为联系概率(复概率)，联系概率(复概率)中的i是主事件和伴随事件在随机试验过程中相互转换的纽带，最后用实例说明联系概率(复概率)在概率推理中的应用.

1 概率的联系数表示

联系数是集对分析中给出的一个概念，其基本形式［13］是

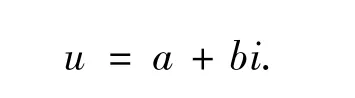
式中:a，b∈［0，1］，a+b=1，i∈［－1，1］.

1.1 大数概率与即或概率

1.1 .1 大数概率

定义1 设A表示随机事件，则A在某次随机试验中发生的可能性大小称为概率，用P(A)表示，0≤P(A)≤1.基于概率论中的大数定律可知，P(A)是A在随机试验次数n趋于无穷大时A出现的频率(k为A出现的频数)的近似值，本文把这种基于大数定律的概率称为随机事件A的大数概率，简称概率.

1.1 .2 即或概率

定义2 若随机事件A在某次随机试验中发生的概率为P(A)，0≤P(A)≤1，则A在某次随机试验中不发生而发生的可能性大小1－P(A)称为A的即时或然概率，简称即或概率.

1.2 概率的联系数表示

根据文献［13］，随机事件A在某次随机试验中发生的可能性大小P(A)与不发生的可能性大小1－P(A)可以联系数化为

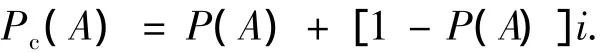
式中:Pc(A)表示联系数意义下事件A在某次随机试验中发生的可能性大小P(A)(A的大数概率)与不发生的可能性大小1－P(A)(A的即或概率)的联系和(也称联系概率)，其原理和定义将在下文阐述.

2 随机性的来源与随机事件

2.1 实验

设一盒子里仅装有a个白球(a≥1)，令事件A是“任抽一个球是白球”，显然 A是必然事件，即P(A)=1.现在向盒子中放入b个黑球(b≥1)，这时的事件 A就从必然事件变为随机事件，相应的P(A)=1变为P(A)＜1.

从以上实验中得到以下结论.

1)基于现象的结论.事件A的随机性来自于盒子中加入了另一种颜色的球.因为实验表明:当盒子中只有白球时，事件A“任抽一个球是白球”是必然事件;但当盒子中加入黑球后，事件A就成为了随机事件，这说明事件A的随机性来自于黑球.

2)对现象进行抽象后的结论.事件的随机性来自2个事物的联系，是事物联系的一种属性.因为实验表明:当盒子中只有一种颜色的球时，事件A“任抽一个球是白球”是必然事件;但当盒子中加入另一种颜色的球后，事件A就成为了随机事件，这说明事件A的随机性来自于2个事物间的联系.

结论2)可以较为规范地表述为:事件A的随机性源自于随机试验中2个互不相容事件A与的一种联系.由此得到了一个新的随机事件定义.

2.2 随机事件

2.2 .1 随机事件的定义

定义3 具有随机性的事件称为随机事件.

已有的概率统计文献把随机事件定义为可能出现或可能不出现的事件［2，16］，这是人们对于事件的随机性停留在现象表面的一种认识.这种认识虽然具有客观性，但容易引导人们把注意力集中于一个事件上，而忽视了与这一事件密切相关的另一事件，进而忽视这2个事件的相互关系.事实上，正是由于2个不同事物的同时存在，并由这2个事物引发的2个互不相容事件的相互关系导致了随机性.当然，在忽视了事件的随机性的来源以后，也就无需对这2个随机事件出现与否的影响因素进行分析.

由定义3易得出以下推论.

推论 随机事件必具有随机性.

证明 用反证法，设随机事件没有随机性，但这与定义2相矛盾，所以随机事件必具有随机性.

2.2 .2 随机事件成对存在定理

定理 任一随机试验中的随机事件成对存在.

证明 设事件A是某一随机试验中的随机事件，根据定义1和前述推论可知，该随机事件A必具有随机性.再根据实验显示的事件随机性的产生原理可知，随机性是2个事件的一种关系，因此在随机试验中的随机事件A与随机事件成对存在，证毕.

这里需要注意的是，上述定理指的是随机事件的存在状态，并非指随机事件的表现状态.事实上，当2个随机事件是互不相容事件时，就存在的意义上成对存在，否则不称其为随机事件;但在表现意义上则互不相容，一个出现时，另一个就不出现.

由于随机事件成对存在，为研究方便起见，再给出定义4.

定义4 在随机试验中，根据问题的要求被首先关注的事件称为主事件(也称第一关注事件或正事件);与主事件互不相容的另一事件称为该主事件的伴随事件(也称第二关注事件或负事件)，统称伴随事件.

3 联系概率(复概率)

定义5 基于联系数形式的联系概率(复概率).用联系数a+bi形式表示的随机事件A的概率称为联系概率(复概率).

若用Pc(A)表示联系概率(复概率)，令a=P(A)，b=P()，1］，则有Pc(A)=a+bi=P(A)+P()i.这里 i的定义域与第 1 节中的定义域有所不同，原因在下文解释.

定义6 基于事件的联系概率.把随机试验中主事件A的概率P(A)和伴随事件的概率P()写成联系数P(A)+P()i，称此联系数为随机事件A与的联系概率(复概率)，记为

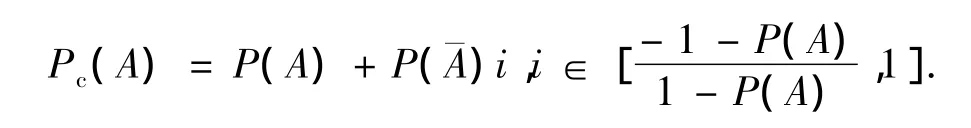
定义7 基于概率的联系概率(复概率).把随机事件A的大数概率P(A)与A的即或概率P()和的乘积联系起来的代数和称为联系概率(复概率).

在同一问题中，基于事件的联系概率(复概率)和基于概率的联系概率(复概率)，其实是同一联系概率的2种不同表述，说明如下.

例1 设盒子中有2个白球，3个黑球，令事件A为“任抽一球是白球”，事件为“任抽一球是黑球”，把A看作主事件，则是A的伴随事件，A与是互不相容事件，A∩=Ø.从基本事件空间这个角度看，P(A)=2/5，P()=3/5，任抽一个球的结果或是A发生或是发生;从事件角度看，P(A)=2/5，P()=3/5，所以 P(A)+P()i=2/5+(3/5)i;从概率的角度看，因为P(A)=2/5，所以1 －P(A)=3/5，同样有 P(A)+P()i=2/5+(3/5)i.

Pc(A)=P(A)+P()i=2/5+(3/5)i=1，

解得这时i=1.当实际抽到的球是黑球时，站在主事件A的角度看，其相应的联系概率Pc(A)=P(A)+P()i=2/5+(3/5)i= －1，解得这时i= －7/3.如果以作为主事件，把A看成的伴随事件，则相应的联系概率(复概率)为 Pc()=P()+P(A)i=3/5+(2/5)i.这时如果任抽一球是黑球，则有

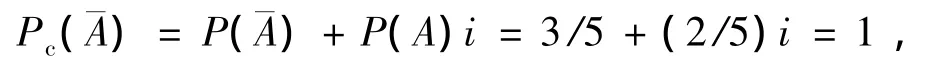
解得i=1;如果任抽一球是白球，则有 Pc()=P()+P(A)i=3/5+(2/5)i= －1，解得 i= －4.

可见在同一问题中选择不同的事件作为主事件，把与之不相容的另一事件作为该主事件的伴随事件，它们的联系概率表达式不同，i的取值也随之不同，这是容易理解的.但由此又引出了一个新概念——负概率，为此给出以下定义.

定义8 随机试验中，设事件A为主事件，而实际试验结果出现事件，A∩=Ø，则称出现随机事件的概率P()为相对于主事件A的负概率.

由定义8可见，所谓主事件A的负概率并非是P(A)的负值，也就是 P()≠ －P(A).有关负概率的性质及其运算规则将另文讨论.

4 联系概率(复概率)在不确定性推理中的应用

文献［17］介绍的基于概率的不确定推理方法如下.

设有如下产生式规则:

则证据(或前提条件)E不确定性的概率为P(E)，基于概率的不确定性推理的目的是，求出在证据E下结论H发生的概率P(H|E)，这时采用式(1)计算.

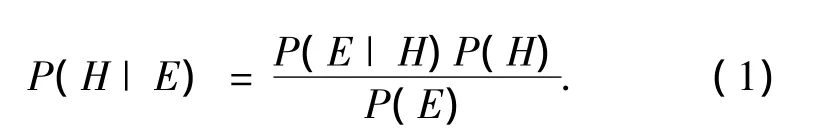
式中:P(E)是前提E的概率，P(H)是H的先验概率，P(E|H)是H成立时E出现的条件概率.

若一个证据E支持多个假设H1，H2，…，Hn，即

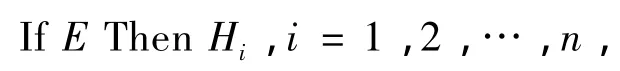
则有贝叶斯公式得

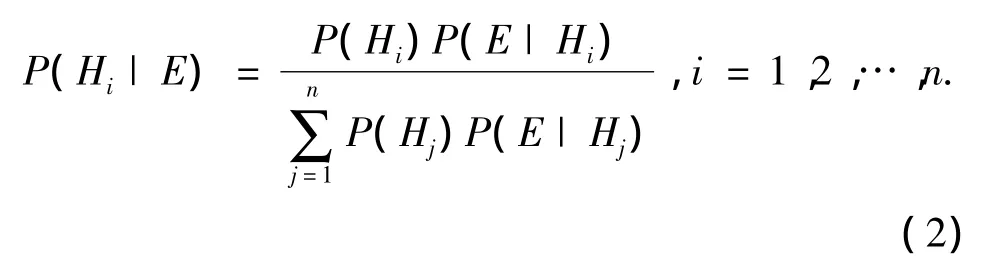
若有多个证据 E1，E2，…，Em和多个结论 H1，H2，…，Hn，并且每个证据都以一定程度支持结论，则

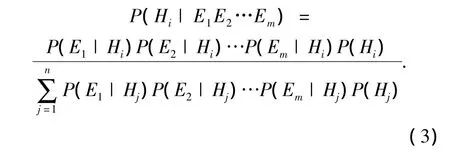
因此，只要已知Hi的先验概率P(Hi)及Hi成立时证据E1，E2，…，Em出现的条件概率

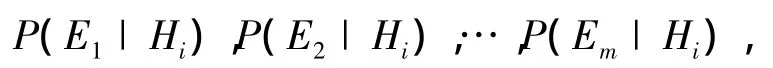
就可利用式(3)计算出在出现E1，E2，…，Em情况下Hi的条件概率P(Hi|E1E2…Em).

例2 设H1、H2、H3为3个结论，E是支持这些结论的证据，且已知

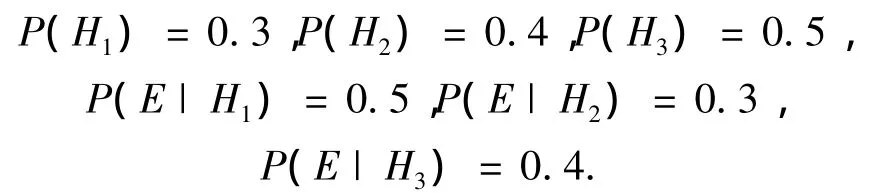
求P(H1|E)、P(H2|E)和P(H3|E)的值.

根据式(2)可得

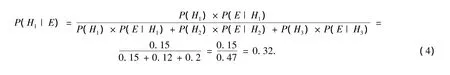
同理可得

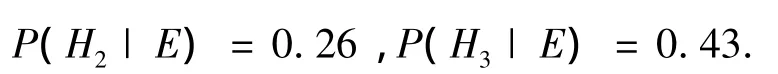
计算结果表明，由于证据E的出现，H1成立的可能性稍有增加，而H2、H3成立的可能性却有不同程度的下降.

以上是文献［17］中的计算结果，下面按本文给出的概率联系数化的角度进行计算分析.

1)由于 P(Hk)≠1(k=1，2，3)，所以 Hk是随机事件，根据随机事件的成对存在定理，可知存在随机事件 ¯Hk，且 Hk与 ¯Hk是互不相容事件，所以P(¯Hk)=1 － P(Hk);因此，以 Hk作为主事件，¯Hk为伴随事件，则以Hk作为主事件的联系概率为P(Hk，¯Hk)=P(Hk)+［1 －P(Hk)］i，也就是有

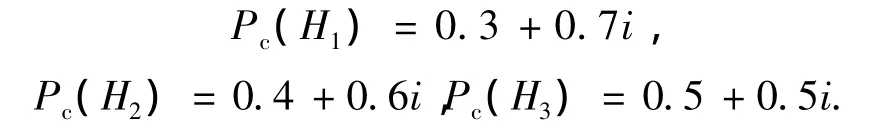
由于 0.7 ＞0.3，0.6 ＞ 0.4，0.5=0.5，所以在计算 i的取值后，Pc(Hk)有可能比P(Hk)大，也有可能比P(Hk)小.这一情况包含了前面式(2)所得到的“由于证据E的出现，H1成立的可能性稍有增加，而H2、H3成立的可能性却有不同程度的下降”这个结果;但由于没有考虑证据E的作用，所以计算结果过于粗糙，为此进入第2)步.

2)先把P(E|Hk)改写成联系概率Pc(E|Hk)的形式，得

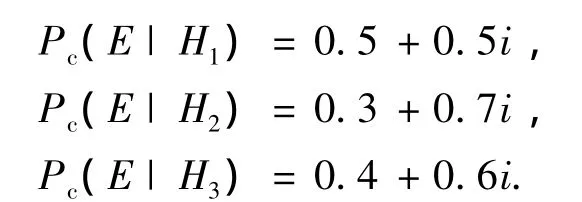
再根据式(2)得

根据集对分析，如果不计不确定性的层次性，可令i=i2，于是上面的计算结果简化为

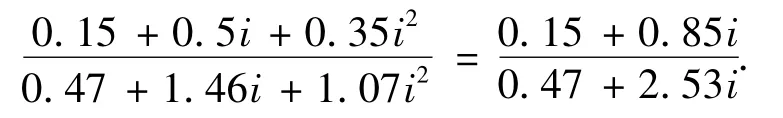
由于以上计算结果中的分母是由3个归一化的联系数相加而成，多出了因归一化而产生的3－1=2个i.其原因可看如下数值例子:

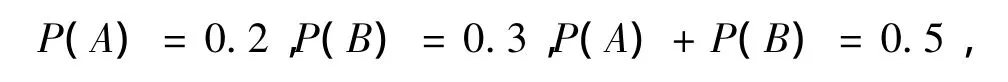
把P(A)联系数化为联系概率，则得Pc(A)=0.2+0.8i，同理有 Pc(B)=0.3+0.7i，按普通加法运算法则有

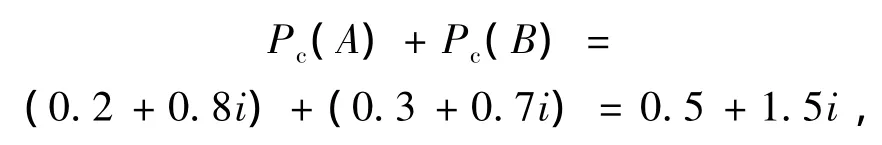
由于把 P(A)+P(B)=0.5 联系数化得 0.5+0.5i，所以要从 0.5+1.5i中减去 2－1=1个 i.为此在0.47+2.53i中减去 2 个 i，得计算结果为

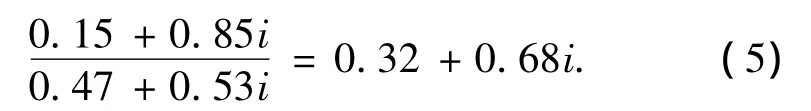
将式(5)与式(4)对照，看出只要把式(4)的0.32联系数化为 0.32+0.68i就是式(5).同理有

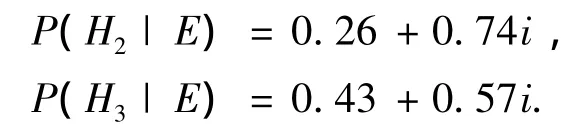
因此可以作如下分析.

1)由于 0.68 ﹥ 0.32，0.74 ﹥ 0.26，0.57 ﹥0.43，所以 H1、H2、H3成立的不确定性大于成立的可能性.

2)计算过程显示出，计及证据E后的结论H1、H2、H3中含有2次不确定性，因为在计算结果中含有i2.这与直观相符，因为证据E本身具有不确定性，结论H1、H2、H3在不计及证据E时已具有不确定性(1次不确定性)，在证据E下的结论H1、H2、H3当然就更具有不确定性(2次不确定性).

基于概率的不确定性推理分析的难点在于其中的证据不确定性和结论不确定性，有了联系概率这个概念之后，这种不确定性分析就具体表现在对i的分析上.但如何结合一个具体的问题展开有关i的分析，包括i的物理意义、构成与分解、取值规律、层次特性、以及对推理结果的影响主要来自1次不确定性还是2次不确定性等，则要具体和深入研究.不言而喻，联系概率的提出和应用，为在不确定性推理中开展证据不确定性和结论不确定性的分析提供了一个平台.

5 结束语

本文引进大数概率和即或概率的概念，借助实验揭示了事件的随机性源自于事物(事件)与事物(事件)的关系，给出了随机事件成对存在定理和联系概率(复概率)的概念(之所以也称联系概率为复概率，是因为集对分析联系数a+bi在形式上与复数一样)，并且指出了负概率的意义(以主事件A为参考事件时出现事件的可能性大小).所有这些新的概念，为概率论的理论和应用创新开辟了新途径，也为人工智能不确定性推理提供了新思路.至于在已知P(A)情况下如何通过i的分析和联系概率(复概率)的计算，预测和调控随机试验中A与的转换，将在另文进行研究.

［1］李德毅.不确定性人工智能［M］.北京:国防工业出版社，2005:1-400.

［2］王梓坤.概率论基础及其应用［M］.北京:科学出版社，1979:218-219.

［3］赵克勤.集对分析及其初步应用［M］.杭州:浙江科技出版社，2000:44-64.

［4］赵克勤，宣爱理.集对论——一种新的不确定性理论方法与应用［J］.系统工程，1996，14(1):18-23.

ZHAO Keqin，XUAN Aili.Set pair theory—a new theory method of non-define and its applications［J］.Systems Engineering，1996，14(1):18-23.

［5］赵克勤.集对分析的不确定性理论在AI中的应用［J］.智能系统学报，2006，1(2):16-25.

ZHAO Keqin.The application of uncertainty systems theory of set pair analysis(SPA)in the artificial intelligence［J］.CAAI Transactions on Intelligent Systems，2006，1(2):16-25.

［6］王文圣，金菊良，丁晶，等.水资源系统评价新方法——集对评价法［J］.中国科学 E辑:技术科学，2009，39(9):1529-1534.

WANG Wensheng，JIN Juliang，DING Jing，et al.A new approach to water resources system assessment—set pair analysis method［J］.Science in China，Series E:Technological Sciences，2009，39(9):1529-1534.

［7］ZHOU Ze’nan.Decision support system based on set pair analysis and its application［J］.Engineering Sciences，2007，5(3):76-81.

［8］GAO Feng，CHEN Yingwu.A project risk ranking approach based on set pair analysis［J］.Engineering Sciences，2006，4(3):89-93.

［9］沈定珠.体育用联系数学［M］.深圳:中国教育文化出版社，2007:1-191.

［10］王文圣，李跃清，金菊良，等.水文水资源集对分析［M］.北京:科学出版社，2010:1-183.

［11］米虹，赵克勤.非传统安全集对分析［M］.北京:知识产权出版社，2010:1-218.

［12］刘保相.粗糙集对分析决策模型与应用［M］.北京:科学出版社，2010:1-185.

［13］郭瑞林.作物育种同异理论与方法［M］.北京:中国农业科学技术出版社，2011:1-294.

［14］赵克勤.试论集对分析与概率论的关系［C］//数学及其应用文集.长沙:湖南科技出版社，1995:253.

［15］赵克勤.二元联系数A+Bi的理论基础与基本算法及在人工智能中的应用［J］.智能系统学报，2008，3(6):476-486.ZHAO Keqin.The theoretical basis and basic algorithm of binary connection A+Bi and its application in AI［J］.CAAI Transactions on Intelligent Systems，2008，3(6):476-486.

［16］赵秀恒，米立民.概率论与数理统计［M］.北京:高等教育出版社，2008:1-28.

［17］蔡自兴，徐光佑.人工智能及其应用［M］.北京:清华大学出版社，2010:114-116.