两种IGS精密星历多项式插值方法的比较分析
刘刚,邵楠
(1.重庆市勘测院,重庆 400020; 2.沈阳市勘察测绘研究院,辽宁 沈阳 110004)
1 引言
利用IGS提供的精密星历和钟差参数,可以实现高精度的定位。IGS发布的SP3格式的精密星历通常给出的是15 min或者5 min等间隔的卫星位置和钟差信息,而在实际应用中可能需要任意历元时刻的位置和钟差信息,这就需要利用精密星历提供的等间隔时刻的信息进行内插方法得到特定的历元时刻的卫星位置和钟差,然后再进行后续的计算。因此,高精度、快速实现对精密星历和钟差的内插或拟合就成为了GPS数据处理中的一项基础而重要的内容。
用于内插的方法有很多种,包括:切比雪夫多项式插值、拉格朗日多项式插值、牛顿多项式插值、三角函数多项式插值等。目前在GPS数据处理中,应用比较多的是拉格朗日多项式插值和切比雪夫多项式插值。本文首先对这两种插值方法进行了介绍,然后通过自编程序实现了这两种插值方法并对两种插值方法的结果进行比较分析。
2 切比雪夫多项式插值与拉格朗日多项式插值
2.1 切比雪夫多项式插值
切比雪夫多项式拟合就是根据给定的数据拟合出一个函数,使其在给定点的函数值与给定值之间的方差和最小,且该函数是以切比雪夫多项式为基函数构成的函数[1,2]。
假定欲将在时间间隔[t0,t0+△t]的卫星星历用n阶切比雪夫多项式进行逼近(或标准化),其中t0和△t分别是开始历元和拟合时间区间的长度。为了用切比雪夫多项式对卫星轨道标准化,首先时间t∈[t0,t0+△t]变换成 τ∈[-1,1],变换公式为[3]:
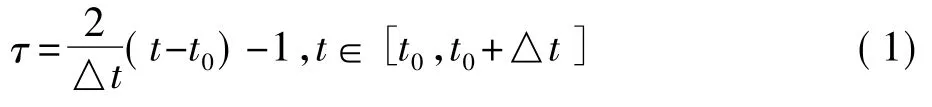
则卫星坐标X,Y,Z分量可用如下切比雪夫多项式表示:

在式(2)中,n为切比雪夫多项式的系数,Cxi,Cyi,Czi分别为X坐标分量、Y坐标分量、Z坐标分量切比雪夫多项式的系数。切比雪夫多项式Ti用以下递推公式确定:

根据精密星历,设卫星的Xk坐标为观测值,则误差方程为:

误差方程的矩阵展开式为:


则有向量表达式:

应用最小二乘法平差中的间接平差,可以得出法方程为:

式(6)中,N=BTPB,fex=BTPfx,此处,权矩阵 P 为单位阵,因此,N=BTB,fex=BTfx,则方程(5)的解为:

此时,X各分量便为切比雪夫多项式拟合系数Cxi。同理,对Y、Z分量完成上述类似的计算便可得到关于某颗GPS卫星在[t0,t0+△t]区间内各坐标分量的切比雪夫多项式拟合系数 Cxi,Cyi,Czi(i=0,1,2,…,n)。通过这三组系数,便可利用(1)~(3)式分别计算得到[t0,t0+△t]时间区间内任意时刻的卫星坐标。
为了检查拟合的质量,还需要对拟合结果进行质量评定。一般来说是利用中误差来评定的,评定公式如下:
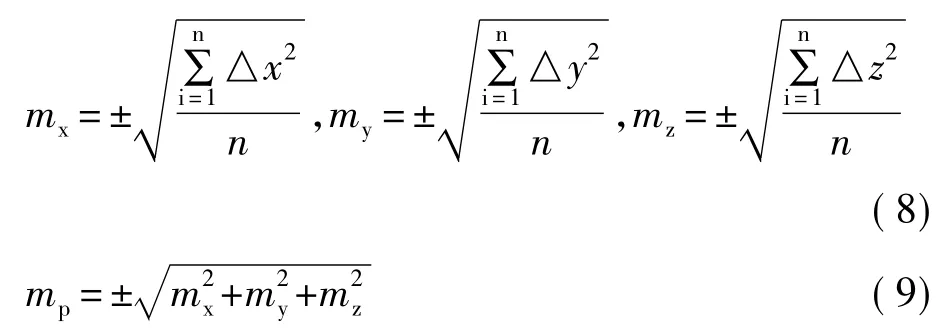
mx,my,mz和 mp分别表示卫星坐标 X,Y,Z 方向上的中误差和点位中误差。
2.2 拉格朗日多项式插值
设 y=f(x)是区间[a,b]上的一个实函数,xi(i=0,1,…,n)是[a,b]上 n+1 个互异实数,且 y=f(x)在 xi处的值为yi=f(xi),则区间[a,b]上任意一点x的n阶拉格朗日插值多项式的代数表达式为[4,5]

点xi(i=0,1,…,n)称为插值节点,包含插值节点的区间[a,b]称为插值区间。
3 计算实例及比较分析
为了比较两种方法的插值精度,作者根据上述插值原理利用VC编制了程序来实现两种插值方法。文中选取了IGS发布的2009年3月29日的精密星历数据作为算例来研究不同阶数多项式下两种插值方法的精度。由于精密星历给出的卫星位置的时间间隔为15 min,因此本文计算中以30 min为时间间隔选取内插点内插计算得到各个内插时间段中间时刻的卫星位置,以便将两种方法内插得到的结果与精密星历给出的卫星位置进行比较,获得两种插值方法的精度。从上述的两种插值原理中可以看出,当采用n阶多项式插值时,至少需要n+1个节点的坐标数据,为了检验坐标内插的质量,选取n+1个节点中间已知坐标的n个点作为插值点,计算出这n个插值点的坐标,与已知值进行比较,检核其精度。作者利用自编程序用两种插值方法分别计算了32颗卫星在不同阶次下各插值点处的平均点位误差,表1给出了不同阶次多项式下两种插值方法在内插时段中心点出的平均点位误差。
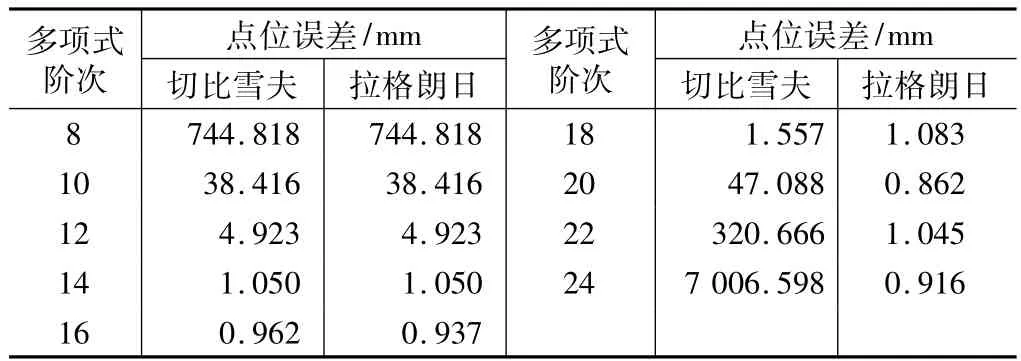
不同阶次多项式内插中心点处精度比较 表1
从表1中可以看出,随着插值多项式阶次的提高,切比雪夫多项式插值的精度先是逐渐提高,当阶次达到20次以后,插值精度迅速降低,这称为高次插值的“龙格”现象。而采用拉格朗日多项式插值,随着多项式阶次的提高,插值精度先是提高,然后趋于稳定。
按照切比雪夫多项式插值时间归化的原理,两种多项式插值结果反映为时间与精度的关系如图1、图2所示,式中T为所取插值点位于整个插值区段的位置,取中心节点处为0,整个插值区段为(-1,1)。

图1 切比雪夫多项式插值结果
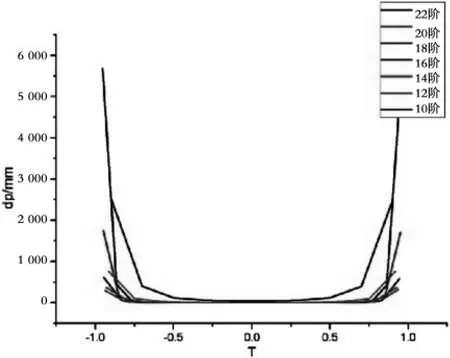
图2 拉格朗日多项式插值结果
图1和图2分别表示了用不同阶次切比雪夫多项式和拉格朗日多项式插值在整个插值区间的精度。从图中可以看出,两种插值方法均表现出两头大中间小的误差分布情况,特别是在10阶、20阶和22阶时,两端处的误差跳跃较大。从图中也可以看出,两种插值方式从10阶上升到20阶时,走势基本一致,当多项式阶次上升到22阶时,两种方法表现出不同的走势:切比雪夫多项式插值精度明显变差,随时间变化的趋势也发生了改变,出现了不规则的波动,这是因为阶数太高,使数据噪声纳入了拟合模型,影响了模型的精度[6]。而拉格朗日插值法则保持了之前的走势,离插值中心点较近的地方仍旧保持了较高的精度,在两端处精度迅速下降。为了更好地分析两种插值在高阶时的差异,抽取图形局部放大,如图3所示,可看出在20阶时切比雪夫多项式插值精度显著降低,波动较大,差于拉格朗日插值法。

图3 20阶多项式插值精度对比
由此可以看出,当多项式阶数上升到一定程度后,利用切比雪夫多项式插值的结果不再可靠,而拉格朗日插值法仍旧保持高精度的插值。实验结果显示,利用两种方法进行插值时,采用一定阶次的多项式进行插值,在插值区间范围内,80%左右的插值区间均能取得很好的插值效果。根据这一特性,采用切比雪夫多项式进行插值时,可适当提高阶次以提高插值区间覆盖的范围,在有效范围内,只需一次计算多项式系数进行存储即可直接使用,可以免去多项式系数的重复计算。对于一天的数据,需要衔接前后一天的数据,分为几个时段,分别存储几组系数,在应用中根据所需时间直接调用系数进行计算即可。而对于拉格朗日插值法,在各个不同的时间点上进行插值时需要单独进行运算。
4 结语
本文通过程序实现了利用切比雪夫和拉格朗日多项式对IGS精密星历进行插值的功能,分析了不同阶次多项式对于插值精度的影响,并对两种方法进行了比较。实验数据表明,按照 30 min间隔选取插值节点,在多项式阶次达到10阶以上时,两种方法均能取得毫米级的插值精度,在一定阶次范围内,两种插值方法插值精度相当。当多项式阶次上升到20阶以上时,切比雪夫插值法精度迅速下降,而拉格朗日插值法仍维持较高的精度,说明高次插值时,切比雪夫多项式插值方法“龙格”现象更为突出。根据实验结果,两种插值方法的运算都较简单,精度也较高。在选取插值方法以及多项式阶次时,应根据实际需要拟合时间长度来选择,对于切比雪夫多项式插值法可适当提高多项式阶次以实现较长时段的高精度拟合,而对于拉格朗日插值法,在达到要求的插值精度后,再提高多项式的阶次已无益于插值精度的提高,因此无需采用过高的阶次以提高运算效率。
[1]邱蕾,廖远琴,华向红.基于IGS精密星历的卫星坐标插值[J].测绘工程,2008,17(4):15~18
[2]刘刚.基于精密星历的切比雪夫多项式卫星轨道坐标拟合研究[J].城市勘测,2010(1):53~55
[3]陈正阳,易重海.用切比雪夫多项式进行GPS卫星轨道标准化[J].矿山测量,2002(2):5~7
[4]曹德欣,曹璎珞.计算方法(第二版)[M].徐州:中国矿业大学出版社,2001
[5]朱方生,李大美,李素贞.计算方法[M].武汉:武汉大学出版社,2003
[6]杨学峰,程鹏飞,方爱平等.利用切比雪夫多项式拟合卫星轨道坐标的研究[J].测绘通报,2008(12):1~3

