励磁附加调差对电力系统阻尼特性影响的机理分析

霍承祥，刘增煌，濮 钧

（中国电力科学研究院电力系统研究所，北京 100192）

励磁附加调差对电力系统阻尼特性影响的机理分析

霍承祥，刘增煌，濮 钧

（中国电力科学研究院电力系统研究所，北京 100192）

本文研究了励磁系统附加调差对系统阻尼的影响。将附加调差引入菲利蒲-海佛隆模型，分析附加调差对模型参数的影响。推导出附加调差提供的阻尼转矩系数增量ΔKD随附加调差系数XC变化的曲线为一条二次抛物线，而且这条抛物线的开口方向和位置与励磁参数、发电机参数、运行状况及系统参数有关。证明了此抛物线在以ΔKD为纵轴、以XC为横轴的坐标系中必经过原点，在其他参数确定的前提下，抛物线与横轴的第二个交点是发电机功角的函数。根据此抛物线可全面说明附加调差对系统阻尼的影响情况。现场试验结果与理论推导相符。

励磁系统；附加调差；菲利蒲-海佛隆模型；阻尼；同步转矩；阻尼转矩

前言

励磁系统中的调差称为电压调差率或者无功调差率，我国励磁系统国标[1]对电压调差率的定义是：发电机在功率因数等于零的情况下，无功电流从零变化到额定定子电流值时，发电机端电压的变化率。负载电流补偿器退出后的电压调差率称自然电压调差率。我国一般将负载电流补偿称为附加调差。

在现代广泛采用的快速励磁系统中，由于自然调差率很小，所以附加调差对改善系统电压稳定性、改善发电厂间的无功分配有十分明显的作用。国内外对调差有不少研究，在附加调差对发电机和电力系统无功及电压稳定的影响方面结论比较一致，但在对系统动态行为方面，也就是附加调差是恶化还是改善了系统的阻尼，结论完全不同[2-9]。为了探讨附加调差的应用，就需要对调差的动态行为进行研究, 弄清附加调差的作用机理。

1 菲利蒲-海佛隆模型的拓展

由 K1～K6表示的单机无穷大系统数学模型即菲利蒲-海佛隆模型[10]，该模型未考虑附加调差。单机无穷大系统中发电机各电气量的向量图如图1所示。

图中xe为发电机外部电抗；Vs为无穷大母线电压；Vt为发电机端电压；δ为发电机q轴与Vs的夹角，即发电机功角。另外，电抗xq后的假想电势为EQ。

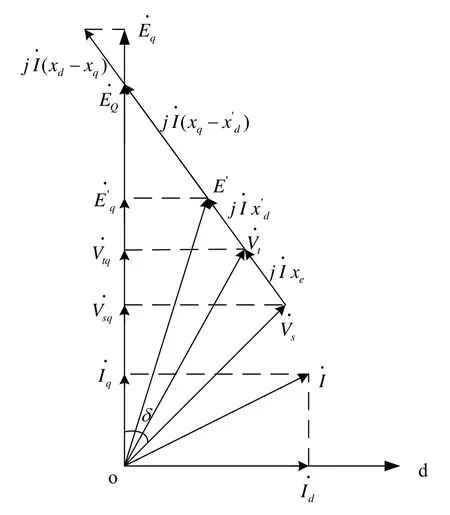
图1 发电机向量图

根据图1可得无功功率的表达式：

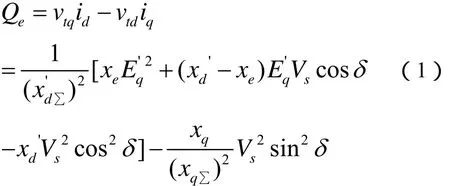
式（1）可以写成δ与 Eq'的偏差方程的形式：

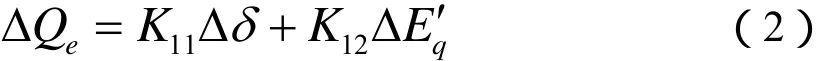
则

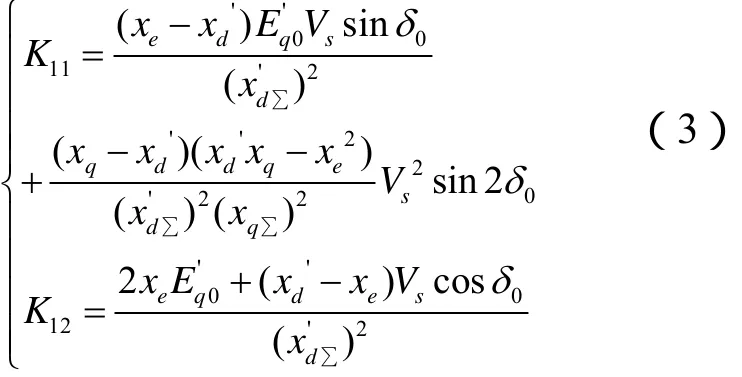
发电机的无功调差公式可以用下式表示：

其中Xc为附加调差系数。

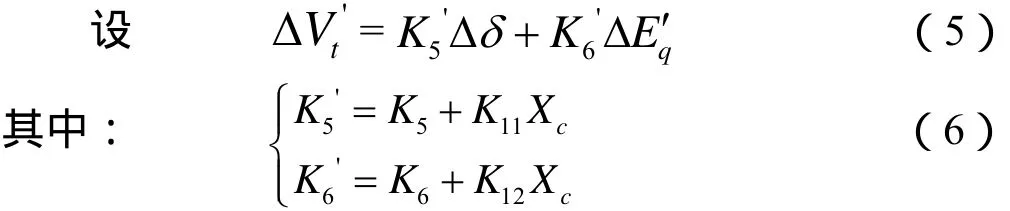
从而得到图2所示考虑附加调差后的菲利蒲-海佛隆模型框图。

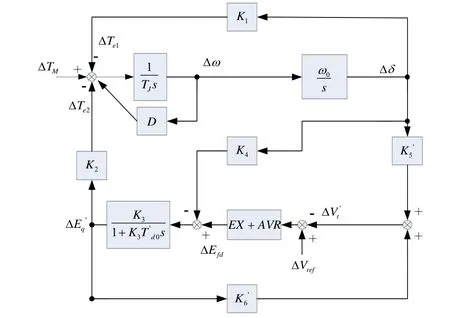
图2 引入附加调差后的菲利蒲-海佛隆模型

假设系统作小振幅正弦振荡，振荡角频率ω1，则以s=jω1代入（7）式可以求出无附加调差时励磁系

统阻尼转矩系数KD(Xc=0)和同步转矩系数KS(Xc=0)：

由图2可见，引入附加调差之后并未改变菲利蒲-海佛隆模型的结构，未对各个系数之间的关系产生影响，但是振荡频率会有所变化。所以只要将式（8）、式（9）中的K5和K6分别用K5′和K6′代替，并且用

2ω代替1ω，就得到引入附加调差后励磁系统阻尼转矩系数KD(Xc≠0)和同步转矩系数KS(Xc≠0)：

如果已知振荡频率，则可以根据式（8）～（11）计算比较 KD(Xc=0)与 KD(Xc≠0)的大小以及 KS(Xc=0)与KS(Xc≠0)的大小。但是，振荡频率本身又是阻尼力矩系数和同步力矩系数的函数。可通过求解系统特征方程特征值的方法来求得振荡频率。

2 附加调差对系统阻尼特性影响的机理分析

下面求解附加调差带来的阻尼转矩系数增量ΔKD与附加调差系数 Xc的关系。由附加调差带来的阻尼转矩系数增量ΔKD为：

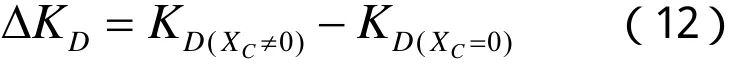
将式（6）代入式（10），再将式（8）和（10）代入式（12），并设：

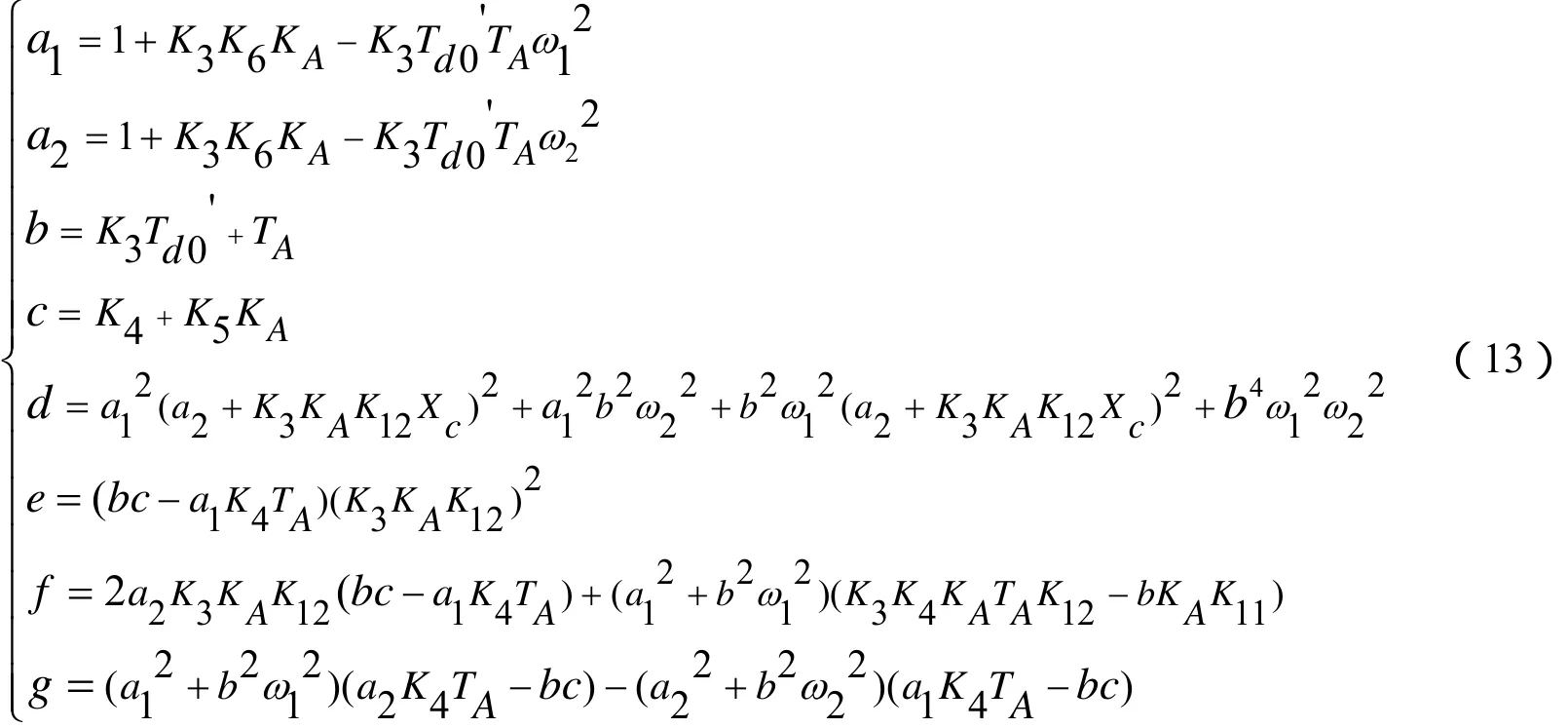
最后整理∆KD的表达式可得：

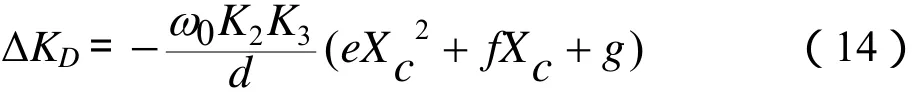
因为 K2、 K3、d均为正数，所以对一定的运行点（系数 K1～K6、K11和 K12确定）和励磁系统参数，在Xc-ΔKD直角坐标平面上，式（14）是一条二次抛物线。e＞0时抛物线开口向下，e＜0时抛物线开口向上，抛物线与Xc轴有两个交点 Xc1和 Xc2。

第一个交点 Xc1=0，是坐标原点。显而易见，Xc=0时，ΔKD=0。

第二个交点 Xc2，理论上可以通过eX2+ fX + g =0求得。但因g本身也受X（通过ccc振荡频率ω2）影响，因此只能通过迭代的方法求得Xc2。考虑到附加调差系数的实际取值范围较小（一般绝对值不大于0.15p.u.），忽略其对振荡频率的影响，即设ω2=ω1，则式（14）可写为：

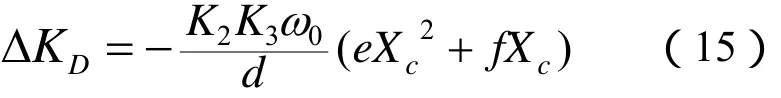
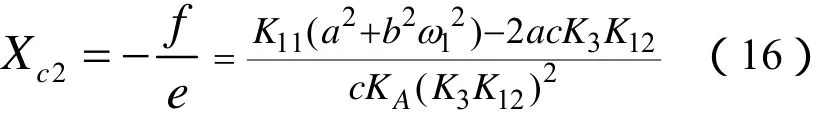
令 Δ KD= 0 可直接求得 X c2：式（16）中，因ω2=ω1，所以a=a1=a2。由式（16）可见 Xc2与发电机参数、运行方式及励磁系统参数有关。

对一台实际运行的机组，其发电机及励磁参数均已确定。根据不同的运行方式，抛物线开口向下可能出现下面3种形式：

（1） X c2＜0，如图3的△KD1、△KD2。

（2） X c2=0，如图3的△KD3。

（3） X c2＞0，如图3的△KD4、△KD5。

由图3可见，在一定的运行点上，附加调差系数符号不变而只改变大小，不仅会改变阻尼转矩系数增量△KD的大小，而且也可能改变△KD的符号。例如，抛物线开口向下且2cX＞0（图3抛物线K△D4），当0＜ Xc＜2cX 时 ∆KD＞0，正附加调差提供正阻尼；当Xc＞ Xc2时 ∆KD＜0，正附加调差提供负阻尼。而在有的运行点上，△KD随Xc单调增加（如图3抛物线△KD5）；有的运行点，△KD会随Xc单调减小（如图3抛物线△KD1）。所以，阻尼增量抛物线的位置随着2cX改变而改变，抛物线在坐标系中位置不同，附加调差对系统阻尼的影响也不同。观察2cX 的表达式（16）发现，在给定发电机参数、外部电抗和励磁参数的条件下，2cX 是功角的函数。因此，对应于一定的发电机、励磁系统参数和调差系数 Xc，运行点不同，附加调差产生的阻尼转矩增量不仅数量上的大小不同，性质（正或负）也可能不同。同一个调差系数，在一个运行点上产生正阻尼，而在另一个运行点上则可能产生负阻尼。

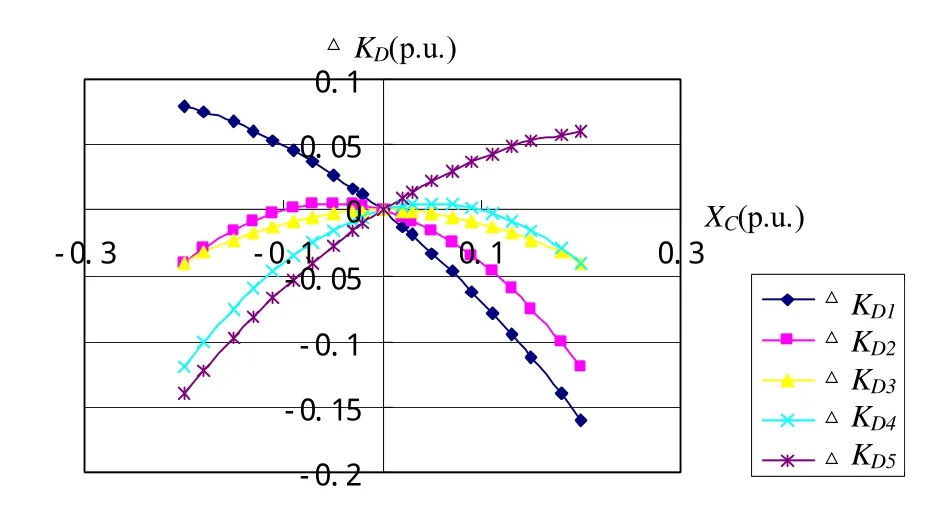
图3 开口向下的抛物线

3 试验

在某实际机组上进行了相关试验，以检验附加调差对发电机阻尼的影响。该机组是额定功率为 27MW的水轮机组，采用自并励励磁方式，发电机和主变压器为单元接线，其主变电抗为 12%。本机组处于某省电网末端，无本地负荷，调差系数的改变对该机组无功功率的影响十分明显。

在相同工况下（有功P=25MW，无功Q=5MVar）进行了发电机电压扰动试验。退出 PSS，分别在调差系数为0和-7%时进行了发电机电压2%阶跃试验，根据有功P的波动来计算发电机阻尼。试验波形见图4、图5所示。采用的阻尼比计算公式为：

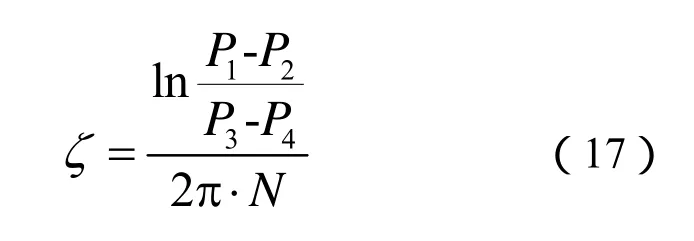
式中：P1是波动图形的第1个峰值；P2是第1个谷值；P3是第N+1个峰值；P4是第N+1个谷值；N是P1至P3的振荡次数。

由图4的有功波动数据可计算出阻尼比为0.0876，由图5有功波动数据可计算出阻尼比为0.0929。可见-7%调差时有功振荡阻尼明显弱于 0调差时的阻尼，前者阻尼比是后者阻尼比的0.943倍。

该水轮机组位于功率送端，运行于较大工况时，负附加调差提供负阻尼、正附加调差提供正阻尼。对应于图3中△KD5这一类型，与前文推导相符。

图4 无PSS时电压2%阶跃，调差系数XC=-7%

图5 无PSS时2%阶跃，调差系数XC=0

4 结论

总结起来，可以归纳为如下几点结论：

（1）附加调差会对系统阻尼产生影响。附加调差提供阻尼的正负，不仅与附加调差系数的正负有关，而且也与附加调差系数的绝对值大小、发电机参数、运行工况、系统参数及励磁参数有关。

（2）一定的附加调差，在不同的发电机运行状况下，有可能提供正阻尼，也有可能提供负阻尼或零阻尼。

（3）发电机运行状况下，附加调差不同时，有可能提供正阻尼，也有可能提供负阻尼或零阻尼。

（4）附加调差提供的阻尼转矩系数增量∆KD随附加调差系数 Xc变化的曲线是一条经过 Xc－∆KD坐标系原点的抛物线。在其他条件确定的情况下，抛物线与横轴（ Xc轴）的第二个交点随发电机功角变化而单调变化。

（5）机组试验结果与理论分析结果吻合。

[1] GB/T 7409.1-2008, 同步电机励磁系统定义[S].

[2] 刘取. 电力系统稳定性及发电机励磁控制[M]. 北京：中国电力出版社，2007.

[3] Murdoch A．Excitation control for high side voltage regulation [C]//Proceeding of 2000 IEEE Power Engineering Society Summer Meeting．Seattle，Washington，USA：IEEE，2000：311-316.

[4] Carson W T．Line drop compensation, high side voltage control-why not control a generator like a static var compensation[C]//Proceeding of 2000 IEEE Power Engineering Society Summer Meeting，Seattle，USA：IEEE，2000：307-310．

[5] Kitamura H．Improvement of voltage stability by the advanced high side voltage control regulator[C]//Proceeding of 2000 IEEE Power Engineering Society Summer Meeting．Seattle，Washington，USA：IEEE，2000：278-284．

[6] Davies J B．High side voltage control at manitoba hydro[C]//Proceeding of 2000 IEEE Power Engineering Society Summer Meeting．Seattle，Washington，USA：IEEE，2000：271-277．

[7] Kosterev D．Design，installation，and initial operating experience with line drop compensation at john day powerhouse[J]．IEEE Trans on Power Systems，2001，16(2)：261-265．

[8] 程林，孙元章，贾宇，等．发电机励磁控制中负荷补偿对系统稳定性的影响[J]．中国电机工程学报，2007，27(25)：32-37．

[9] Nelson Martins. The New Cigre Task Force on Coordinated Voltage Control in Transmission Networks[C]//Proceeding of 2000 IEEE Power Engineering Society Summer Meeting. Seattle,Washington, USA. July 2000: 278-285.

[10] Prabha Kundur. 电力系统稳定与控制 [M]. 北京：中国电力出版社，2002.

[11] 马大强. 电力系统机电暂态过程[M]. 北京：水利电力出版社，1988.

审稿人：孙玉田

The Principle of the Influence on the Power System Dynamic Damping Caused by the Reactive Current Compensation

Huo Chengxiang, Liu Zenghuang, Pu Jun
(China Electric Power Research Institute, Haidian District, Beijing 100192, China)

excitation system; reactive current compensation; philips-heffron model; damping;synchronous torque; damping torq

TM761

A

1000-3983(2012)02-0053-05

2011-08-10

霍承祥(1978-)，2004年毕业于清华大学电气工程专业，获硕士学位；现从事电力系统试验建模、电力系统稳定与控制等方面的研究，工程师。

Abstrct: Based on the single-machine-infinite-bus system, the effect of Reactive Current Compensation (RCC) on the system damping is studied. First of all, RCC is added into the Phillips-Heffron model and the influence on the model and parameters caused by RCC is analyzed.Then the study proves that the relationship of the damping torque coefficient increment (∆KD)provided by RCC and RCC coefficient (XC) is a second-degree parabola. Furthermore the open direction and position of the parabola are related with the excitation parameters, the parameters and the operating conditions of the generator and the system parameters. Finally the conclusion is given:the parabola passes through the zero point in the coordinate system whose abscissa axis is XCand vertical axis is ∆KD, and the second crossing point between the parabola and the abscissa axis will change with the power angle of generator if the other parameters are determinate. The effect of RCC on the dynamic damping can be explained comprehensively based this parabola. The field test result is in concord with the analysis.