水轮机调速系统转矩系数分析

曾 云，张立翔，徐天茂，郭亚昆

(1. 昆明理工大学建筑工程学院，昆明 650051；2. 昆明理工大学计算中心，昆明 650051；3. 阿伯丁大学工程学院，英国阿伯丁 AB24 3UE)

水轮机调速系统转矩系数分析

曾 云1，张立翔1，徐天茂2，郭亚昆3

(1. 昆明理工大学建筑工程学院，昆明 650051；2. 昆明理工大学计算中心，昆明 650051；3. 阿伯丁大学工程学院，英国阿伯丁 AB24 3UE)

水轮机调速系统包括水轮发电机组对象和调速器，其小波动暂态的阻尼特性是影响机组稳定性的主要因素，本文对调速系统附加机械阻尼以及同步力矩的形成机理和计算进行了系统的研究。以典型调速器结构为例，建立包括机组对象和控制器在内的水轮发电机组线性化模型框架，给出了水轮机及其调速系统附加机械阻尼系数和同步力矩系数的计算方法。分析机组运动特性和阻尼系数的构成，定义了稳态和动态阻尼系数两种类型，并提出以机电振荡模式特征根近似计算机组自振频率的方法。仿真表明，适当调整调速器PID参数可以提高机组动态阻尼系数，本文所提出的计算方法是有效的。

调速系统；转矩系数；动态阻尼；机电振荡

前言

传统三阶发电机模型中的等效阻尼系数D是影响发电机及电力系统稳定的重要参数。文献[1]从发电机及系统等值电路、派克方程等不同途径推导出了不同详细程度的系数D的计算公式。当发电机与其他设备相连后阻尼特性发生变化，其作用等效于在原发电机中增加了附加阻尼项[2-6]。同样，当发电机与原动机及其调节系统相连后，必然存在相应的附加机械阻尼，这一问题在文献[7，8]中均提到，但未做进一步的研究。而电力系统小扰动的研究中，通常忽略机械力矩的变化，即忽略了原动机及其调节系统的影响。

对于高阶复杂系统，阻尼系数的计算是困难的，为此，De Mello F P提出一种转矩系数计算方法[9]，将与ω同相位的力矩分量定义为阻尼力矩，与功角δ同相位的力矩分量定义为同步力矩。该方法物理概念清晰，应用方便，获得了较好的应用[10-12]。近年来一些基于在线检测获取阻尼特性的方法也获得了应用[13]。

本文以典型调速器结构为例，将水轮发电机组作为一个整体，采用转矩系数分析方法，研究机组转矩系数的变化。重点分析了由水轮机及其调速系统产生的附加机械阻尼的计算方法，结合仿真研究了附加机械阻尼系数的变化特点和调速器参数的影响，得出了一些结论。

1 数学模型

1.1 水轮机及引水系统模型

以混流式水轮机为例，以传递系数构成的线性化模型如下：

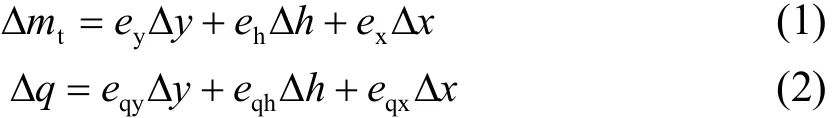
式中，ey、eh、ex分别是水轮机力矩对导叶开度、水头、机组转速的传递系数；eqy、eqh、eqx分别是水轮机流量对导叶开度、水头和机组转速的传递系数；∆mt为机组力矩增量标幺值；∆h、∆y分别为水头、导叶开度增量标幺值；∆x是机组转速增量标幺值，在数值上等于发电机角速度增量标么值∆ω，从定义看，它们符号相反。

方程(1)，(2)可以采用图1来表示。

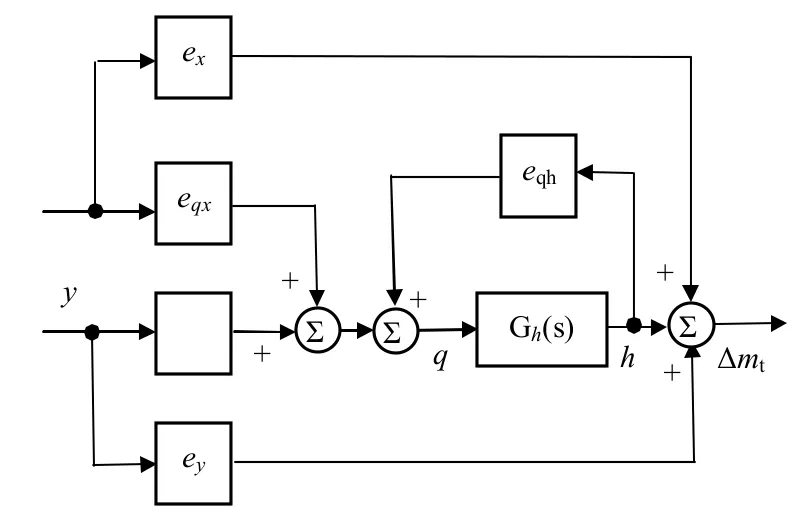
图1 水轮机线性模型

由图可见，系统可分解为两路单输入单输出系统的迭加。

-∆ω→∆mt的传递函数为：

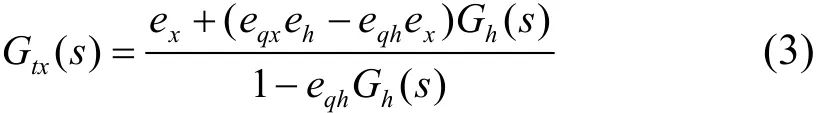
y→∆mt的传递函数为：

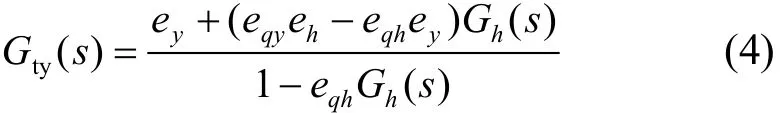
Gh(s)是水轮机流量q到水头h的传递函数。引水系统考虑单机单管的简单情况，采用忽略水头损失的弹性水击模型，其传递函数为[8]：

式中：Tr是水击传播时间(s)；hω是管道特征系数。

1.2 调速器模型

采用文献[14]给出的并联 PID调速器结构如图 2所示。

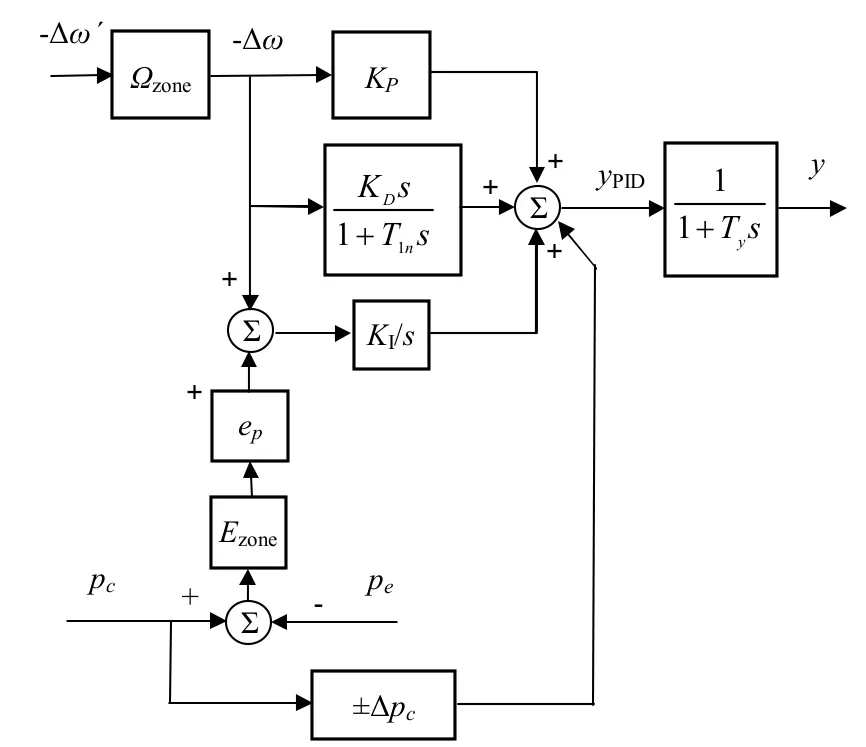
图2 典型并联PID调速器结构图

图2中，Ωzone表示人工设置的转速死区；Ezone是人工设置的功率死区；pc和pe分别是给定功率和实测功率相对值；∆pc是功率前馈；Ep是调差率；KP，KD，KI分别是并联PID控制器的比例，微分和积分常数,T1n是实际微分环节的时间常数(s)；bp是调差系数；Ty是主接力器时间常数(s)。

调速器输入的机组频率偏差定义为给定频率减去实测频率，即 ∆f=f0-f，而且给定频率通常采用频率基值f0=50Hz。在发电机运动方程中机组角速度偏差相对值定义为实测角频率减去角频率基值，即∆ω=ω-ω0。这两者的标幺值数值相等，符号相反, ∆ω=-∆f。

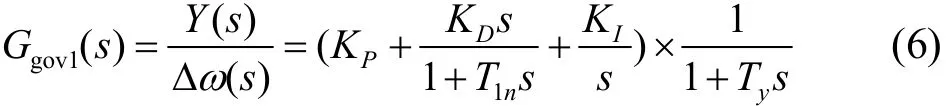
调速器输入∆ω到主接力器位移的传递函数为：假定给定功率pc不变，来自电网侧的扰动使得发电机端口功率pe变化，产生的功率扰动为:

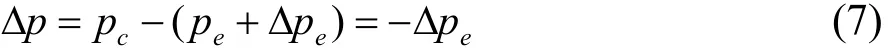
忽略人工功率死区，由功率扰动到主接力器位移的传递函数为：

上式中，忽略了功率前馈环节的影响。由于功率前馈环节有多种算法，增加了后续算法的不确定性。本文的目的在于给出一种附加转矩系数的分析方法，因此，暂不考虑各型调速器的一些细节。

1.3 发电机及电网模型

对于单机无穷大系统，发电机采用三阶实用模型，励磁系统为静止励磁系统并用一阶惯性环节描述，其线性化模型如图3所示[10]。

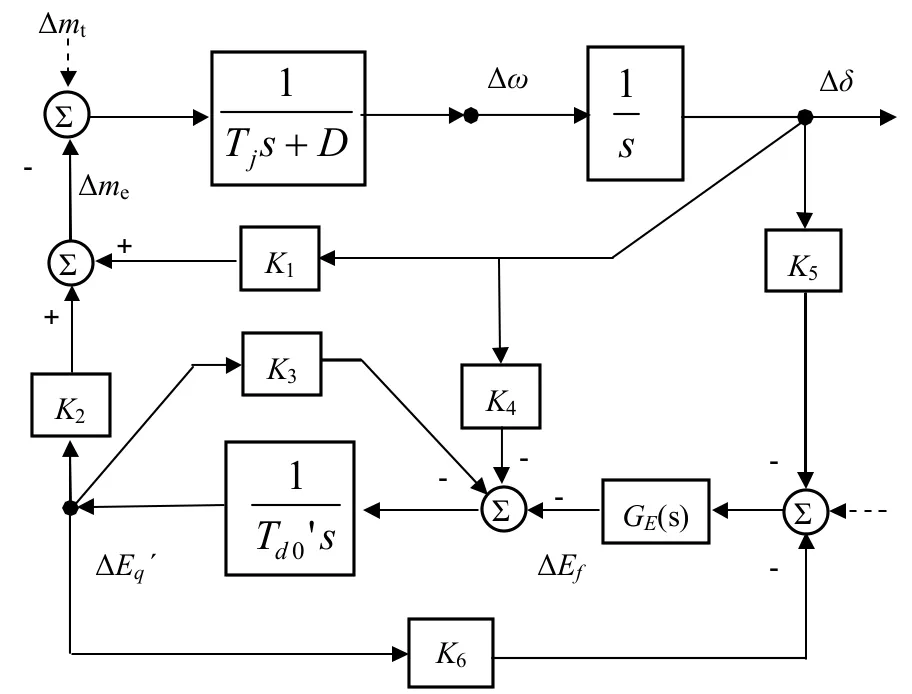
图3 单机无穷大系统发电机线性模型

图3中，K1, …, K6为常数；Tj为机组惯性时间常数；∆δ是发电机功角增量(rad)；D是等效的机械阻尼系数；GE(s)是励磁系统传递函数，本文中励磁系统为GE(s)=KE/(1+TEs)，KE是放大系数，TE是时间常数(s)。

可以直接写出从∆δ→∆me的传递函数为：

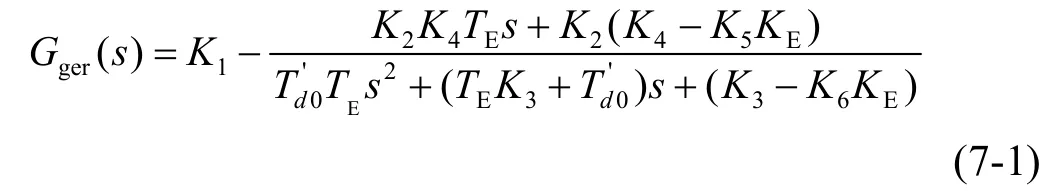
将上述各部分组合，即可得到完整的水轮发电机组线性模型，如图4所示。

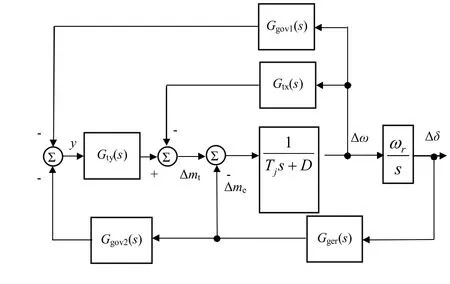
图4 水轮发电机组线性模型

图4中，Ggov2(s)这一支路的输入是一种近似，即在并网运行条件下，ω≈1，则∆pe≈∆me。这一支路反映了机端功率扰动引起的调速器的随动调节作用，而在多数研究中都被忽略了。事实上，在发电机机端，来自电网侧的扰动通常同时包括频率扰动和功率扰动，因此，考虑这一支路的意义是明显的。

图4给出的线性化模型，可以理解为一种结构概念模型。根据不同研究目的，这一概念模型可做不同的细化处理。

2 力矩系数

2.1 附加机械力矩系数

当机组发生振荡时，水轮机力矩增量也可以表示为[7]：

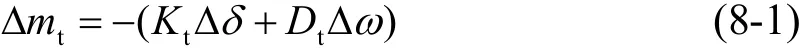
式中，Kt、Dt分别是机械系统在振荡时产生的附加同步力矩系数和阻尼力矩系数。

从图4看，∆ω的变化通过三个通道对水轮机力矩产生影响，具体的表达式为：

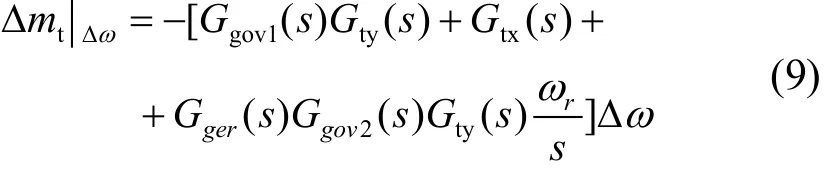
由式(9)可以看出，附加的机械阻尼系数包括三部分，一是由调速器形成的机械阻尼，它主要由调速器的转速调节通道决定；二是机组转速变化引起水轮机力矩变化的传递系数，不依赖于调速器，是水轮发电机组的固有特性。该项数值较小，在多数研究中均忽略不计；三是由调速器的功率反馈通道和发电机传递函数决定。

可在三种情况下计算力矩系数：

（1）假定系统的振荡角频率为ωs，用s=jωs代入式（9），其实部与∆ω同相位，为阻尼力矩项。由于∆ω和 ∆δ相位相差 90°，可采用关系式：j∆ω=-∆δωs/ωr代入上式的虚部，得到与∆δ同相位的同步力矩项。或者直接化成式(8)的形式，得到相应的同步力矩系数Kt和阻尼力矩系数Dt。

显然，由此而导出的附加同步和阻尼力矩系数是系统振荡频率ωs的函数。

（2）在系统发生机电振荡的时候，假定机电振荡模式的特征根为s=α+βi，以s代入式(9)，可得到一个复数表达式，其实部与∆ω同相位，虚部为i∆ω。

利用 ωr∆ω=(α+βi)∆δ导出虚部的替换表达式：

利用式(10)可以将力矩表示为式(8)的形式，则∆ω的系数为Dt阻尼系数，∆δ的系数为同步力矩系数Kt。

（3）当机组进行调节时，由于机组系统本身的特性，机组的运动实际上是一种衰减振荡过程，此时，力矩系数的计算，可以按机组机电振荡模式下的计算方法同（2）进行计算。

2.2 发电机力矩系数

采用文献[9]提出的方法，发电机电磁力矩可以写成以下形式：

式中：Ks，Ds分别是同步力矩系数和阻尼力矩系数。

从图3可以得到，由于∆δ变化引起磁通变化而造成的电磁转矩变化为：

同样，可在三种情况下计算力矩系数：

（1）用 s=jωs代入上式，其实部与 ∆δ同相位，为同步力矩项。采用关系式 j∆δ=ωr∆ω/ωs代入上式的虚部，得到与 ∆ω同相位的阻尼力矩项。或者直接化成式(11)的形式，得到相应的同步力矩系数 Ks和阻尼力矩系数Ds。

（2）当系统发生机电振荡时，假定机电振荡模式的特征根为：s=α+βi，以s代入式(12)，可得到一个复数表达式，其实部与∆δ同相位，虚部为i∆δ。

利用 ωr∆ω=(α+βi)∆δ, 由此导出虚部的替换表达式：

（3）稳态工况时，s→0（s＝0）：

即稳态时的同步力矩系数为：

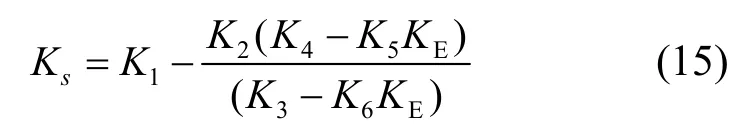
同样，当机组进行调节时，机组的运动实际上是一种衰减振荡过程，此时力矩系数的计算，可以按机组机电振荡模式下的特征根进行计算。

3 机组运动特性

发电机组运动方程为：

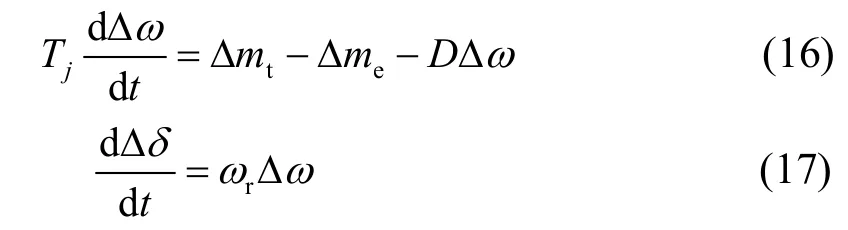
式中：ωr是额定角速度。

将式(8)，(11)代入式(16)，整理得到：

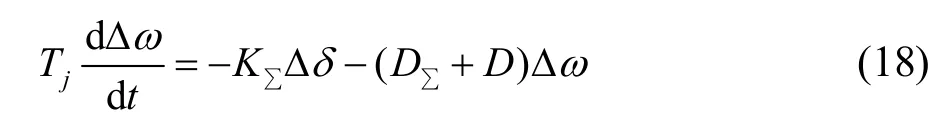
式中：KΣ=Kt+Ks是总的同步力矩系数；DΣ=Dt+Ds称为动态阻尼系数，是由机组暂态过程中励磁控制器和调速器所产生的。

将式(17)代入式(18)，机组运动方程整理为二阶系统标准形式：

参数∆δ的自然振荡频率为：

阻尼比：

当 0＜ζ＜1时，方程(19)的特征方程的根为共轭复根：

上述表达式有以下三点值得注意：

（1）机组的自然振荡频率，主要由同步力矩系数KΣ和机组惯性时间Tj决定。若系统振荡频率接近机组自振频率附近时，将引发共振现象[15]。因此，在设计阶段，预先计算或预估发电机所在电网的机电振荡模式的振荡频率，通过选择适当的机组惯性 Tj，使得机组的自振频率偏离机电振荡频率，避开可能的共振区，也是提高系统稳定性的措施之一。

（2）当系统振荡频率接近机组固有振荡频率时，将出现共振现象。另一方面，机组的机电振荡模式反映了机组与电力系统连接形成一个复杂系统后所具有的振荡特征。研究表明，机电振荡也是一种共振现象。因此，可以利用其他方法所获得的机电振荡模式的特征根，来近似得到机组的振荡参数。设机电振荡模式特征根为s=α+βj，β就是阻尼振荡频率，则机组的自然振荡频率和阻尼比分别为：

（3）阻尼系数 DΣ的变化，主要影响振荡的衰减速度，即阻尼比。从 DΣ的构成看，其中的 Dt和 Ds都与控制器结构相关。因此，从控制器结构设计角度研究改善机组阻尼特性的问题值得深入研究。

4 阻尼系数D的变化

4.1 D的含义

发电机三阶模型的假设中，忽略D、Q绕组动态，为了近似计及D、Q绕组动态中的阻尼作用以及转子运动中的机械阻尼，在转子运动方程中加入一项等效阻尼项D∆ω。从定义看，D包含了发电机的机械阻尼和电气阻尼，由于发电机机械阻尼计算困难，在实际分析中一般取为零，发电机电气阻尼采用文献[1]推荐的近似公式进行计算：

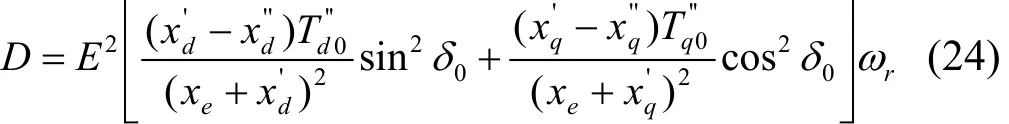
发电机等效阻尼系数D实际上是稳态时的电气阻尼系数，与稳态初始工况有关，不随振荡工况变化。

4.2 系数D的扩展

从机械力矩的作用性质可以知道，在机械力矩中同步力矩分量是很小的，如果忽略同步力矩分量，则式(8)中，机械力矩近似可以等效为附加机械阻尼，即：

则机组运动方程简化为：

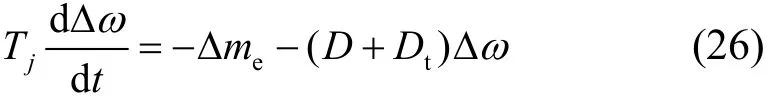
于是，有以下结论。

在机组运动方程中，水轮机及其调速系统的作用，可以近似采用附加阻尼项Dt∆ω来等效，其作用可以并入原运动方程的阻尼项之中，以扩展的阻尼系数来表示。

这一结论的意义在于，在发电机和电力系统小扰动研究中，如果要计及原动机及其调速系统的作用，只需修改发电机运动方程中的阻尼系数取值，而不增加系统的微分方程阶数，即不增加系统求解难度，即可等效这种作用。这一结论为现有发电机及电力系统稳定分析和控制设计中，忽略机械力矩的做法，提供了合理的动力学解释。

5 实例研究

5.1 基本参数

基本参数：Tr=1.2，hω=0.2894，TE=1.05，KE=50，Tj=5.9046，Td0'=5.4，Ty=0.5，Ty1=0.1，Tn'=0.1，bp=0.04，KI=0.3，KD=0.35，KP=3，直接计算出D=1.2。

线性化模型中部分参数是随工况变化的，在额定工况下的参数值为：ey=0.7875，eqy=0.8287，eh=1.6713，eqh=0.6896，ex=－1.4237，eqx=0.4492，K1=1.0320，K2=0.9437，K3=0.2328，K4=0.4706，K5=－0.0999，K6=0.5189。

将上述水轮发电机组各环节用状态方程写出，系统矩阵为14阶，在不考虑水轮机及其调速器系统附加机械阻尼时，采用上述实例参数计算出机电振荡模式的特征根为：-0.4242±7.6151i。

5.2 力矩系数的变化

给定不同的系统振荡角频率 ωs，以式(9)和式(12)计算各项阻尼力矩系数的变化。为更直观，将振荡角频率转换成频率的形式，记为Hs=ωs/2π，阻尼系数和同步力矩系数的变化如图5、6所示。

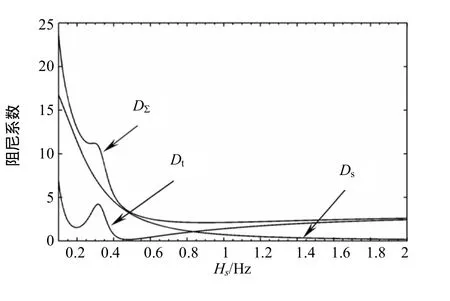
图5 阻尼系数随振荡频率的变化

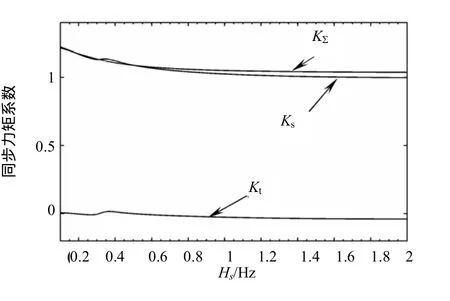
图6 同步力矩系数随振荡频率的变化

从图5和图6可以得出以下结论：

（1）当振荡频率较低时,即系统振荡周期大于控制器的调节周期时，控制器能进行有效的调节，其效果等效于存在较大的动态阻尼系数。例如振荡小于0.1Hz，即振荡周期大于 10s，调速器开始发挥调节作用，其等效的附加机械力矩系数Dt逐渐增大。同样，振荡小于 0.5Hz，即振荡周期大于 2s，励磁控制部分发挥作用，其等效的动态阻尼系数逐步增大。

（2）当振荡频率过大时，例如本例中振荡频率高于 2Hz，即振荡周期小于 0.5s，此时励磁和调速器均不能进行有效的调节，整个机组实际上被拖入强迫的跟随振荡。而此时，调速器部分仍能产生一定的动态阻尼，阻尼系数约为2.5。其原因在于：由于水轮机及其调速器的调节周期较长，当扰动的振荡周期较短的时候，调速器感受到的是非振荡的扰动，或者说是振荡的均值，因此，调速器按既定的方式进行调节，并产生相应的动态阻尼。

（3）同步力矩系数随系统振荡频率变化不大。水轮机及其调速系统产生的同步力矩系数相对较小，在4.2节中考虑的省略是恰当的。

5.3 机电振荡模式

（1）当系统发生机电振荡时，水轮机及其调速系统机械力矩的变化，以s=-0.4242+ 7.6151i 代入式(9)，整理有：

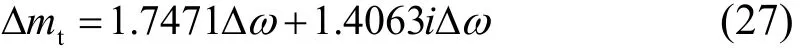
利用替换表达式(10)计算 i∆ω 并带入上式，整理得到:

即发生机电振荡时，水轮机及调速系统产生的附加机械力矩系数为 Dt=1.6687，同步力矩系数Kt=0.0045。与图5、图6对应频率下的力矩系数是一致的。

（2）当系统发生机电振荡时，发电机及其励磁系统力矩的变化，以s=-0.4242+ 7.6151i 代入式(12)有：

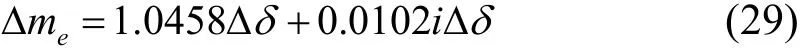
利用替换表达式(13)，整理得到：

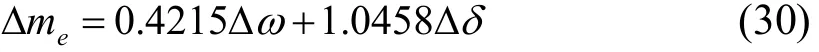
发生机电振荡时，发电机的同步力矩系数Ks=1.0458，阻尼系数Ds＝0.4215。与图5、图6对应频率下的力矩系数是一致的。

（3）从图6可知，由于同步力矩系数随系统振荡频率变化较小，因此，采用式(20)计算机组的自然振荡频率不会产生大的误差。

在机电振荡时，得到的Ks=1.0458, Kt=0.0045, 用(20)式计算，自然振荡角频率ωn=7.4735r/min，即频率为1.1895Hz。

若按机电振荡特征根近似计算，即按式(23)计算得机组自然振荡角频率 ωn=7.6269r/min。与采用式(20)计算的结果相近，两者的误差约为2%。

因此，采用机电振荡模式特征根近似计算机组本身的自然振荡角频率是可行的。

5.4 调速器参数的影响

随着系统振荡频率的增加，振荡周期缩短，尽管调速器不能在一个振荡周期内完成一次调节，但是调节的滞后作用，客观上增加了机组的阻尼，正如图 5所示的动态阻尼逐步增大，并趋于某一定值。为此，这一节通过仿真方法，分析调速器参数对动态阻尼系数的影响。

给定不同的PID参数，Dt随振荡频率的变化如图7所示。

图7中，实线束表示改变KP，虚线束表示改变KD，点划线束表示改变KI。

图7表明，当振荡频率低时，PID参数的变化对动态阻尼系数的变化影响较大。而在机电振荡频率(1.1895Hz)附近，提高PID的比例系数KP可以适当增加系统的阻尼系数Dt，增加微分系数KD会降低Dt。

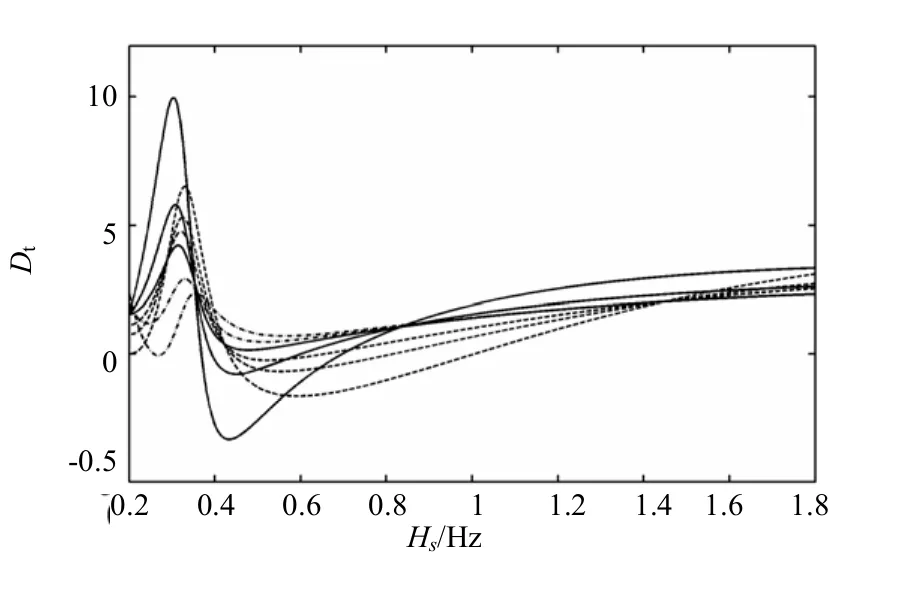
图7 PID参数对Dt的影响

基于这一仿真，从增加阻尼的角度出发，对调速器PID参数的设计有以下建议：

（1）由于机组进行调节时，其调节过程实际上是一种衰减振荡过程，振荡频率就是其固有的阻尼振荡频率，即近似为机电振荡频率。以机电振荡频率为参考，设计PID参数是恰当的。

（2）电力系统低频振荡是一种机电振荡，频率范围一般在0.2～2.5Hz之间。针对不同的振荡频率，采用变参数PID策略，可以利用调速器提高机组的阻尼，进而改善机组和电力系统的稳定性。

6 结论

本文重点讨论了水轮机及其调速器附加机械转矩系数的形成和计算问题，主要结论如下：

（1）附加的同步转矩系数可以忽略。

（2）水轮机及其调速系统的作用，可以近似采用附加阻尼项Dt∆ω来等效，其作用可以并入原运动方程的阻尼项之中，以扩展的阻尼系数来表示。

（3）在机电振荡频率附近，水轮机及其调速器的时滞可以产生附加的动态阻尼，而且该项阻尼可以通过调整调速器PID参数适当的改变。

（4）水轮机及其调速器系统附加机械阻尼与调速器的结构形式有关。

[1] 韩英铎, 王仲鸿, 陈淮金. 电力系统最优分散协调控制[M]. 北京：清华大学出版社, 1997.

[2] 王鑫, 刘宪林, 崔召辉. 扩展 c1～c12模型及 SVC阻尼特性再认识[J]. 电力系统自动化设备, 2008,28(8)：60-64.

[3] 李鹏, 余贻鑫, 贾宏杰, 等. 小扰动电压稳定的P-H 模型及振荡阻尼因子[J]. 中国电机工程学报,2003, 23(12)：19-22.

[4] Milanovic J V. Damping of the low-frequency oscillations of the generator: dynamic interactions and the effectiveness of the controllers[J]. IEE Proceedings: Generation, Transmission and Distribution, 2002, 149(6)：753-760.

[5] WANG H F, SWIFT F J. Application of the Phillips-Heffron model in the analysis of the damping torque contribution to power systems by SVC damping control[J]. Electrical Power and Energy System, 1996, 18(5)：307-313.

[6] SHALTOUT A A, Abu Al-FEILAT K A. Damping and synchronizing torque computation in multimachine power systems[J]. IEEE Transactions on Power Systems, 1992, 7(1)：280-286.

[7] 余耀南. 动态电力系统[M]. 北京：中国水利电力出版社, 1983.

[8] 沈祖诒. 水轮机调节系统分析[M]. 北京：中国水利水电出版社, 1991.

[9] DeMELLO F P, CONCORDIR C. Concepts of synchronous machine stability as affected by excitation control[J]. IEEE Transactions on Power Apparatus and Systems, 1969, 88(4)：316-329.

[10] KUNDUR P. 电力系统稳定与控制[M]. 北京：中国电力出版社, 2002.

[11] 李鹏, 余贻鑫. 电网低频振荡研究回顾及对阻尼概念的再认识[J]. 南方电网技术研究, 2005,1(3)：28-36.

[12] 刘宪林, 柳卓, 娄和恭. 基于直观线性化模型的同步发电机电磁力矩分析[J]. 电力自动化设备,2006, 26(10)：1-6.

[13] HASSAN G, CLAUDIO C. On-line damping torque estimation and oscillatory stability margin prediction[J]. IEEE Transactions on Power Systems,2007, 22(2)：667-674.

[14] 魏守平, 王雅军, 罗萍. 数字式电液调速器的功率调节[J]. 水电自动化与大坝监测, 2003, 27(4)：20-22.

[15] 曹荣章, 王力科, 曾继伦. 三峡电站调速系统对电力系统低频振荡的影响[J]. 电力系统自动化,1996, 20(12)：4-9.

审稿人：朴秀日

Analysis of Torque Coefficients on Hydroturbine Governing System

ZENG Yun1, ZHANG Lixiang1, Xu Tianmao2, GUO Yakun3
(1.Construction Engineering College, Kunming University of Science and Technology, Kunming 650051, China; 2.Computing Center, Kunming University of Science and Technology, Kunming 650051, China; 3. School of Engineering, University of Aberdeen, AB24 3UE, UK)

Hydroturbine governing system is composed by the object system of hydroturbine generating sets (HTGS) and governor, its damping characteristics in small disturbance transient is a mainly factor for HTGS stability, the forming mechanism and calculating of its additional mechanical damping and synchronous torque are studied in this paper. Taking a classic structure of governor as case, the linearization model frame of HTGS is composed including the object system and governor, the calculation methods of torque coefficients for the additional mechanical damping and synchronous torque of the hydroturbine and its governing system are proposed. The steady state and dynamics coefficients are defined by analyzing motion characteristics of HTGS and composing of damping coefficients, and then the natural frequency of vibration of HTGS can be calculated approximately by the eigenvalue of electromechanical oscillation mode. Simulation results show that proper adjustments PID parameters of governor can improve the dynamic damping coefficient, the proposed calculation method is effective.

governing system; torque coefficient; dynamic damping; electromechanical oscillation

TK730.4+1

A

1000-3983(2012)02-0058-07

国家自然科学基金资助项目(50839003, 50949037,51179079)

2011-07-12

曾云（1965-），1985年毕业于昆明理工大学水动专业，1994年获河海大学工学硕士学位，2008获博士学位，主要研究方向为水力机组稳定与控制，教授。