基于改进GM(1,1)和SVM的长期电量优化组合预测模型

宋晓华，祖丕娥，伊静，刘达

(华北电力大学 经济与管理学院，北京，102206)

电量的预测对电力建设规划和宏观经济发展至关重要，因此，如何提高预测精度一直是研究者关注的问题。目前，对长期电量进行预测时主要使用回归分析、时间系列、灰色系统理论和支持向量机等方法。考虑到时间序列仅适用于需求变化比较均匀的数据源，线性回归分析预测精度低，而非线性回归分析计算开销大，预测过程复杂，因此，选用灰色预测方法和支持向量机方法进行中长期电量组合预测。灰色GM(1,1)预测模型具有要求数据少、不考虑分布规律和变化趋势、运算方便等优点，然而，灰色预测模型过多的依赖电量历史值，在数据离散程度比较大时，预测精度不高[1]。为此，本文作者对原始数据进行平滑处理以改进灰色预测模型。支持向量机预测方法可以较好地解决小样本、非线性、高维数等实际问题，且具有结构简单、全局最优、泛化能力较好等优点，预测精度较高[2-3]。近年来，组合预测方法成为预测领域中一个重要研究方向，组合预测模型能较大限度地利用各种预测样本信息，有效地减少单个预测模型中环境随机因素的影响，提高预测精度[4]。但在组合预测模型中，各单一预测模型权重系数的确定至关重要。考虑到蛙跳算法具有较强的全局收敛能力、局部搜索细致和较强的鲁棒性[5]，且不需要借助问题的特征信息，因此，本文选取蛙跳寻优算法求得各组合预测模型的权重，以提高预测精度。

1 优化组合预测模型建模原理

组合预测[6-7]是指将几种预测方法所得的预测结果，选取适当的权重进行加权平均的一种预测方法。组合预测可以综合利用各单项预测方法提供的信息，集成不同信息来源的预测结果，从而能最有效地提高预测精度。本文选择改进GM(1,1)和支持向量机2种预测模型进行中长期电量预测，其基本原理如下。

设yi为第i年的实际电量(i=1, 2, …, n，n为预测电量的年数)，则由 n年电量观测值可得时间序列(yi)l×n。设fik为第k种方法第i年的电量预测值(k=1,2, …, K)， eik=yi-fik为第k种方法第i年电量预测值的预测误差，ωk为第k种方法权系数的估计值，yˆi为组合预测值，则有：

组合预测模型权重的基本原理是基于误差平方和最小的固定权系数组合预测模型，公式如下：

目前国内外对电量组合预测的研究较多，多采用等权平均组合预测法、方差-协方差优选组合预测法等，但等权平均组合预测法各模型权重相等，没有优选的概念，方差-协方差优选组合预测法得出的权值很不稳定。而蛙跳算法具有参数少、计算速度快、全局寻优能力强等优点，为此，选用蛙跳算法进行优化组合预测模型的权重，优化组合预测模型[8]。即采用蛙跳算法对组合预测模型式(2)进行优化，求出组合预测模型的最优权系数kω，然后，将权系数kω代入式(1)即可得到误差平方和最小的最优组合预测值。具体流程图见图1。

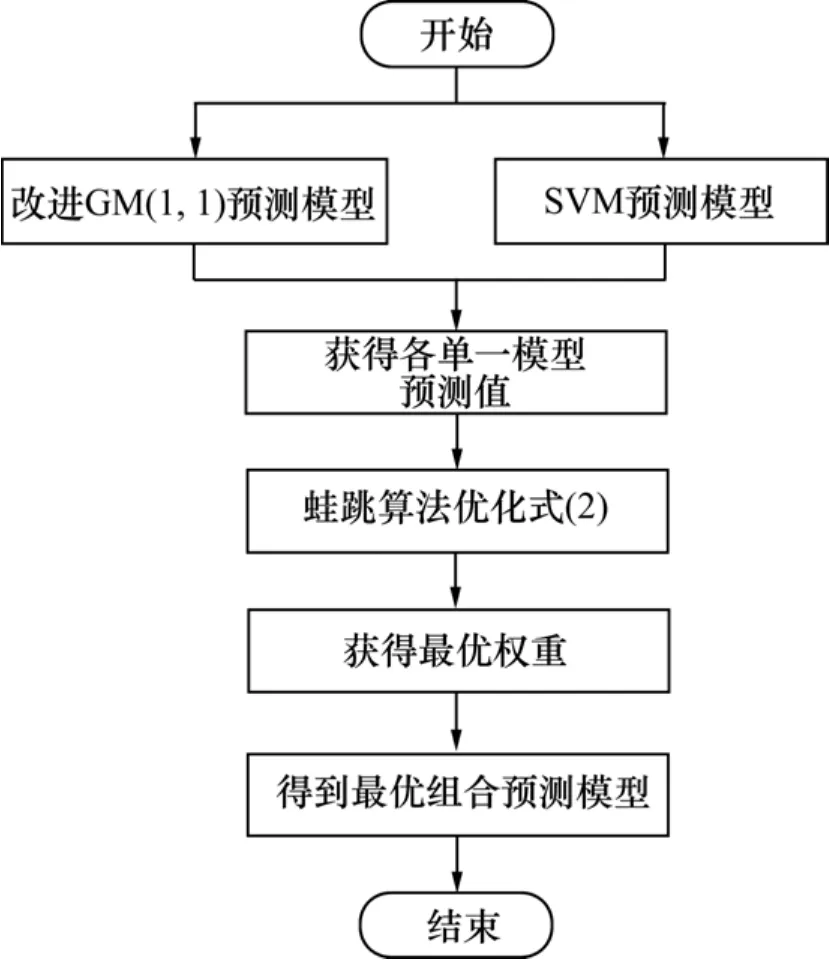
图1 优化组合预测模型流程图Fig.1 Flow chart of optimal combined forecasting model

2 优化组合预测模型建模过程

2.1 改进灰色预测模型

灰色模型是利用历史数据列建立微分方程模型。GM(1,1)模型是最常用的一种灰色模型，由1个只包含单变量的一阶微分方程构成。

灰色模型通过对原始数据作累加生成，使生成的数据列具有指数增长的规律。对生成后的数列建立微分方程模型，求得微分方程的时间响应函数，累减还原即可得到原始数列的灰色预测模型。原始数列的灰色预测模型为：

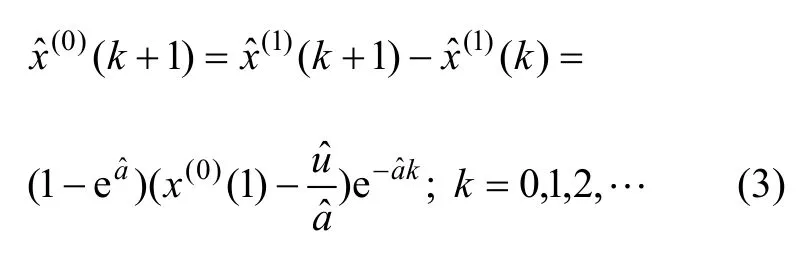
当灰色预测模型在数据离散程度较大时，精度较低，为此，有必要对灰色预测模型进行改进。灰色预测改进的途径一般有改造原始数列、选取初值、改进灰色模型、改进技术方法等。为了降低数据的不平滑度，强化原始数列的大致趋势，选取滑动平均法对数据进行平滑处理来改进灰色预测模型，以提高预测数据的拟合程度。记原始数列为{x0(t)}, t=1, 2, …, n，则滑动平均计算公式为：

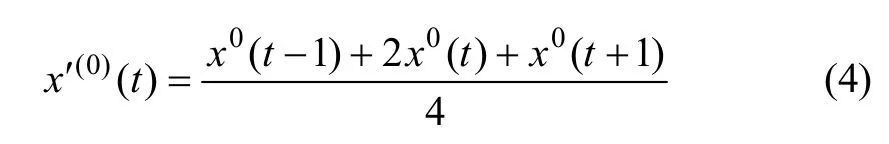
对于2个端点，可采用下式进行计算：

式中：x0为原始数列值； x′0为原始数列滑动平均后的值。原始数据经过滑动平均处理后既增加了当前数据的权重，又避免了数值过度波动，使预测数据拟合度效果更好。

2.2 支持向量机预测模型

支持向量机方法是近期提出的一种较新的智能算法[9]，是建立在统计学习理论即 VC维理论和结构风险最小化原理基础上的一种小样本学习方法，具有要求确定参数少、在理论上有全局最优的唯一解的特点。此外，由于支持向量机在小样本下具有良好的泛化能力，因此，更加适合中长期电量预测。支持向量机回归函数为：

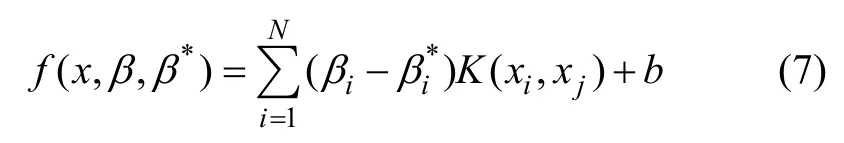
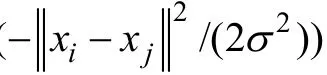
2.3 优化组合预测法

蛙跳算法是一种新兴的群体智能优化算法，多应用于函数优化、参数优化、组合优化等方面[10-11]。它的基本原理是：在D维搜索空间内，随机产生一个青蛙种群。设第i只青蛙(解)表示为 Xi= (xi1,xi2,… ,xiD)。计算种群中个体的适应度并进行降序排列，然后，将整个青蛙种群划分为M个子种群，即第1只青蛙进入第1个子群体，第2只青蛙进入第2个子群体，依此类推，直到第M只青蛙进入第M个子群体，再将第M+1只青蛙划进第1个子群体，一直将青蛙全都划分进入子群体为止[12-14]。然后，各子群体进行局部搜索。子群体迭代时，首先明确子群体内最差个体Xworst、最优个体 Xbest以及整个种群的最优个体 Xglobal，然后，仅对子群体Xworst进行更新，更新策略为：

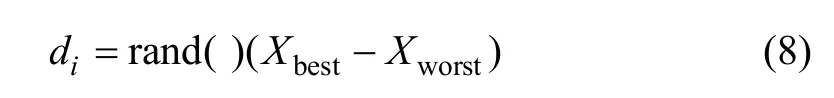
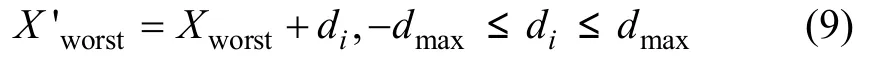
3 模型应用实例

3.1 样本选择

采用本文所提出的基于改进 GM(1,1)和 SVM 的优化组合预测模型，利用我国1991-2010年全国实际电量为样本进行实证分析。其中：1991-2005年电量用于训练学习，2006-2010年电量用于测试模型。本文实证研究的物理平台为：PC终端，WINDOWS732位操作系统，MATLAB7.1运行环境。

本文方法中的参数设置为：蛙跳算法的青蛙群体数N=150，子群数M=9，族内更新次数为10，混合迭代次数为 1 000。支持向量机模型中不敏感损失参数ε=0.01，惩罚因子C=150，核宽度σ=1.58。

3.2 实证结果分析

将所提出的基于改进 GM(1,1)和 SVM 的优化组合预测模型方法分别与等权组合预测、方差-协方差优选组合预测、改进 GM(1,1)和 GM(1,1)及支持向量机的预测结果进行比较，以验证本文研究方法的有效性。各模型电量预测结果如图2所示。从图2可见，采用蛙跳优化组合预测模型所得到的电量曲线与其他2种组合模型相比更逼近真实电量曲线，说明本文提出的蛙跳优化组合预测模型更适合中长期电量预测，获得的预测效果更好。

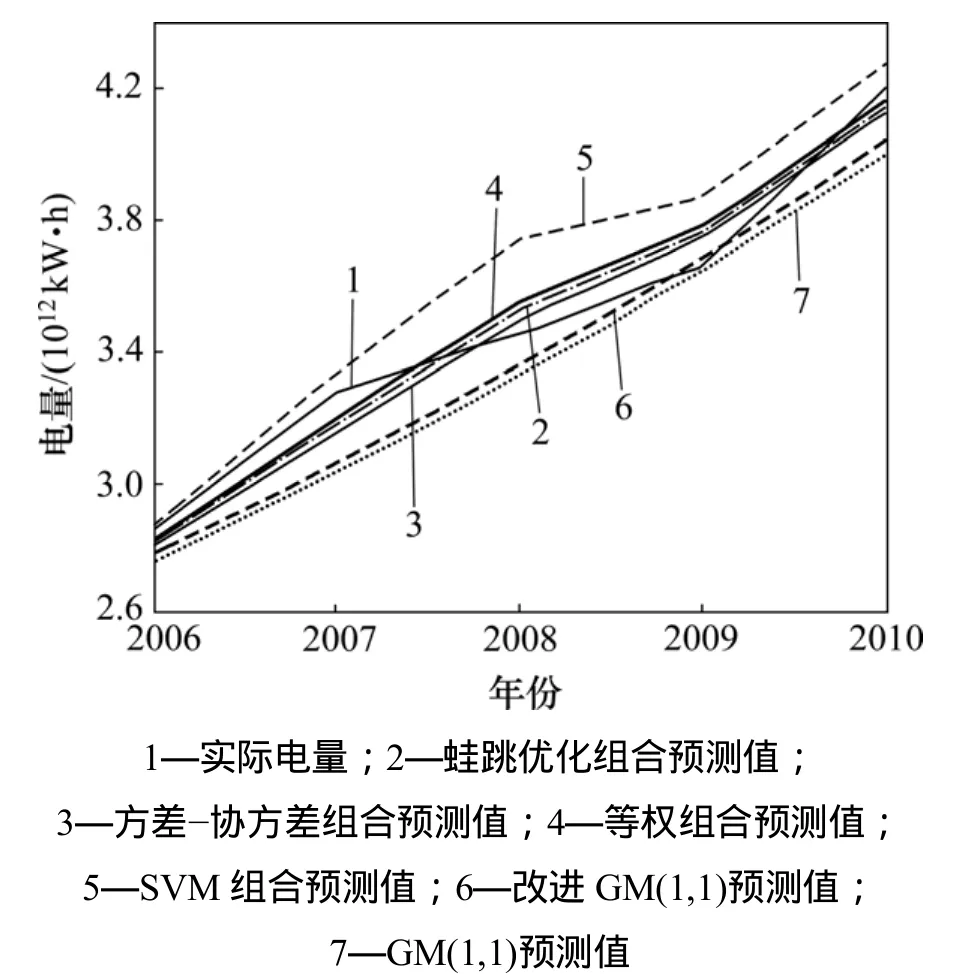
图2 不同预测模型的预测结果Fig.2 Comparison of predictions of different forecasting models

本文所提出的方法与等权组合预测模型、方差-协方差组合模型、改进GM(1,1)，GM(1,1)和SVM的预测误差及精度比较结果如表1所示。

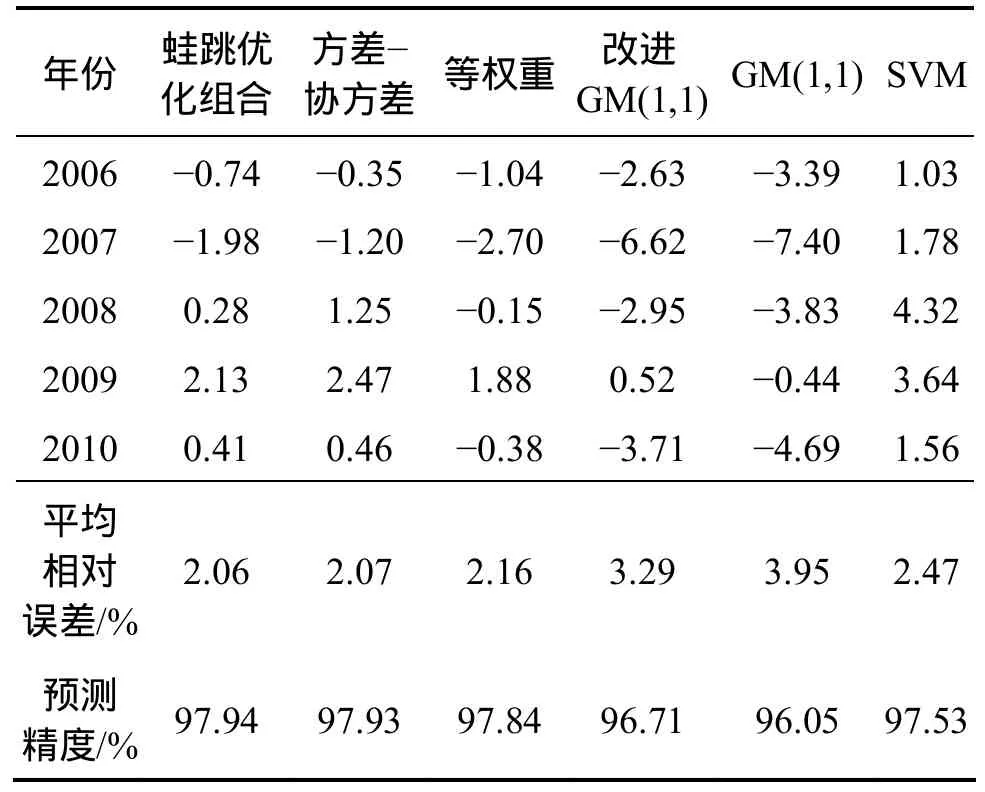
表1 预测误差分析表Table 1 Comparison of forecasting errors with different models

从表1可以看出：改进灰色预测模型的精度比传统灰色预测模型的精度高；而组合预测模型中，利用等权重组合预测方法求解组合预测模型的平均相对误差为2.16%；利用方差-协方差固定权方法求解组合预测模型的平均相对误差为 2.07%；利用基于蛙跳算法的最优组合预测方法的组合预测模型的最大相对误差为 2.13%，最小相对误差为 0.28%，平均相对误差为2.06%。可见：组合预测模型的预测精度比各个单独的数学模型预测精度高，相对误差小。组合预测模型中蛙跳优化组合预测模型的预测精度最高，平均误差仅为2.06%，预测精度达到97.94%。

4 结论

(1) 所提出的基于改进GM(1,1)和SVM长期电量优化组合预测模型，综合了改进GM(1,1)模型和SVM模型各自的优点，能够更好地处理中长期电量预测中周期性和随机性因素的影响，与单一预测方法相比精度更高，更适合中长期预测。

(2) 蛙跳寻优算法具有全局寻优能力强和局部搜索细致的特点。所提出的采用蛙跳寻优算法确定组合预测模型中各模型的权重，克服了组合预测模型中权重求解的局限性，能够更好地发挥组合预测的改进效果。

(3) 所提出的改进GM(1,1)和SVM模型对电力系统中长期电量预测具有较强的预测能力，预测精度比较高，为中长期电量预测提供了一种行之有效的预测方法。

[1] 牛东晓, 营树华, 赵磊, 等. 电力负荷预测技术及其应用[M].北京: 中国电力出版社, 2002: 15-29.NIU Dong-xiao, YING Shu-hua, ZHAO Lei, et al. Electric power load forecasting technology and its application[M].Beijing: China Electric Power Press, 2002: 15-29.

[2] 靳忠伟, 陈康民, 闫伟, 等. 基于支持向量机的中长期电力负荷预测研究与应用[J]. 上海理工大学学报, 2008(2): 130-131.JIN Zhong-wei, CHEN Kang-min, YAN Wei, et al. Study and application of support vector machine to forecast mid-long-term electric power load[J]. University of Shanghai for Science and Technology, 2008(2): 130-131.

[3] 孙翠娟. 基于K型核函数的支持向量机[J]. 淮海工学院学报:自然科学版, 2006, 15(4): 4-7.SUN Cui-juan. Support vector machine based K-type kernel function[J]. Journal of Huaihai Institute of Technology: Natural Sciences Edition, 2006, 15(4): 4-7.

[4] 李建伟, 赵法起, 刘凤玲. 中长期电力负荷的组合预法[J]. 电力系统及其自动化学报, 2011, 23(4): 133-134.LI Jian-wei, ZHAO Fa-qi, LIU Feng-ling. Forecast combining approach of mid-long term power load[J]. Proceedings of the CSU-EPSA, 2011, 23(4): 133-134.

[5] 熊伟平, 曾碧卿. 几种仿生优化算法的比较研究[J]. 计算机技术与发展, 2010, 10(3): 9-12.XIONG Wei-ping, ZENG Bi-qing. Studies on some bionic optimization algorithm[J]. Computer Technology and Development, 2010, 10(3): 9-12.

[6] LIU Shu-liang, HU Zhi-qiang, CHI Xiu-kai. The research of power load forecasting method on combination forecasting model[J]. Information Science and Engineering, 2010(26).

[7] 吴静敏, 左洪福, 陈勇. 基于免疫粒子群算法的组合预测方法[J]. 系统工程理论方法应用, 2006, 15(3): 229-233.WU Jing-min, ZUO Hong-fu, CHEN Yong. A combined forecasting method based on particle swarm optimization with immunity algorithms[J]. Systems Engineering-Theory Methodology Application, 2006, 15(3): 229-233.

[8] 赵鹏军, 刘三阳. 求解复杂函数优化问题的混合蛙跳算法[J].计算机应用研究, 2009, 26(7): 2435-2437.ZHAO Peng-jun, LIU San-yang. Shuffled frog leaping algorithm for solving complex functions[J]. Application Research of Computers, 2009, 26(7): 2435-2437.

[9] Hong W C. Electric load forecasting by support vector model[J].Applied Mathematical Modelling, 2009, 33(5): 2444-2454.

[10] 薛升翔, 贾振红, 杨杰, 等. 用蛙跳算法优化RBF神经网络参数的研究[J]. 计算机工程与应用, 2011, 47(28): 59-61.XUE Sheng-xiang, JIA Zhen-hong, YANG Jie, et al. Using shuffled frog leaping algorithm to optimize the parameters of radial basis function neural network[J]. Computer Engineering and Applications, 2011, 47(28): 59-61.

[11] Rahimi-Vahed A, Dang C M, Rafiei H. A novel hybrid multi-objective shuffled frog-leaping algorithm for a bi-criteria permutation flow shop scheduling problem[J]. International Journal of Advanced Manufacturing Technology, 2009, 41(11):1227-1239.

[12] 贺毅朝, 曲文龙, 许冀伟. 一种改进的混合蛙跳算法及其收敛性分析[J]. 计算机工程与应用, 2011, 47(2): 39-40.HE Yi-chao, QU Wen-long, XU Ji-wei. Improved shuffled frog-leaping algorithm and its convergent analysis[J]. Computer Engineering and Applications, 2011, 47(22): 37-40.

[13] ZHEN Zi-yang, WANG Dao-bo, LIU Yuan-yuan. Improved shuffled frog leaping algorithm for continuous optimization problem[C]//Proceedings of the Eleventh conference on Congress on Evolutionary Computation. Piscataway NJ: IEEE Press, 2009: 2992-2995.

[14] Rahimi-Vahed A, Dang C M, Rafiei H. A novel hybrid multiobjective shuffled frog-leaping algorithm for a bi-criteria permutation flow shop scheduling problem[J]. International Journal of Advanced Manufacturing Technology, 2009, 41(11):1227-1239.