变压器油中气体的多核核主元回归预测模型

唐勇波， 桂卫华， 彭涛

(1．中南大学信息科学与工程学院，湖南长沙 410083;2．宜春学院物理科学与工程技术学院，江西宜春 336000)

电力变压器是电力系统中最重要的设备之一，油中溶解气体分析(dissolved gas analysis，DGA)是电力系统诊断充油电气设备早期潜伏性故障的重要方法。油中气体浓度预测是对用气相色谱法定期检测气体浓度的十分重要且必要的补充，能够提供全面的、重要的、及时的DGA信息，应用这些信息可以保持变压器运行的可靠性［1－3］。

目前，变压器的油中气体浓度预测主要采用灰色模型(grey model，GM)及其改进形式［1－4］。GM在建模时只考虑某种气体的发展变化，缺乏对多种气体的统一考虑，进行预测时难以取得满意的拟合效果。灰色多变量模型(multivariable grey model，MGM)同时考虑了各特征气体的发展变化，取得较好的效果。然而，灰色模型的预测精度一般随数列自身规律的变化而变化，在数列有确定性趋势时预测效果较好，否则预测效果较差［5］。支持向量机(support vector machine，SVM)［6－7］对数据序列分布没有要求，克服了灰色模型的不足，它建立在统计学习理论和结构风险最小化原理基础上，通过结构风险最小化原理来提高泛化能力，不易发生过拟合现象，但SVM的训练需要求解二次规划问题，影响了计算速度。最小二乘支持向量机(least squares support vector machine，LSSVM)［8－9］利用最小二乘法的方法将SVM的学习转化为求解线性方程组问题，提高了学习速度。但是，LSSVM的建模精度过于依赖核函数及其参数的选择。在不同的应用场合，核函数的性能表现差别很大，且核函数的构造或选择至今没有完善的理论依据［10］。文献［11］提出了多核学习的思想，为解决核函数及其参数选择问题提供了可能。文献［12－13］将多核学习的思想应用于研究SVM的回归建模问题，提高了预测建模的精度。

核主元分析方法(kernel principal component analysis，KPCA)是一种非线性特征提取方法，它通过非线性函数将输人映射到高维特征空间，并在高维特征空间中计算主元成分，进行有效地特征提取［14－17］。核主元回归(kernel principal component regression，KPCR)是在核主元分析基础上实现的，通过KPCA方法进行降维处理，把获得的新变量作为多元回归的自变量，进行回归计算与分析［18－19］。到目前为止，尚未见核主元回归方法在变压器油中溶解气体预测中应用的相关文献。

因此，本文将核主元回归引入到变压器油中溶解气体预测中，提出了多核核主元回归(multiplekernel kernel principal component regression，MK －KPCR)的变压器油中溶解气体预测建模方法，通过不同类型核函数的线性加权组合构造新的等价核，采用窗式移动的学习方式，对变压器油中溶解气体进行预测建模，并与灰色多变量模型，主元回归［20］(principal component regression，PCR)及KPCR方法进行比较。

1 核主元回归

1.1 核主元分析

核主元分析的主要思想是通过引入非线性映射Φ将输入空间Xn×m(n为样本数，m为变量数)映射到一个高维特征空间F，然后在高维特征空间计算主元成分，在高维特征空间中得到的线性主元实质就是原始输入空间的非线性主元。设原始数据xi在特征空间F的像为Φ(xi)，则映射数据Φ(xi)的协方差矩阵可以表示为

解决在特征空间的特征值问题

由于特征值λ对应的特征向量v是由特征空间Φ(x1)，Φ(x2)，…，Φ(xn)中的向量所张成，所以存在系数 ai(i=1，2，…，n)满足

通过计算映射数据在特征矢量vr上的投影来计算主元，即

这里＜x，z＞表示x与z的点积，r为主元数。为避免直接计算非线性映射，在特征空间定义核函数矩阵

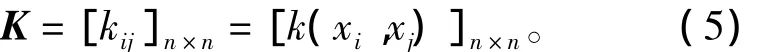
核主元分析的详细求解过程参见文献［15］。

对于核函数的选择，可选高斯径向基核函数

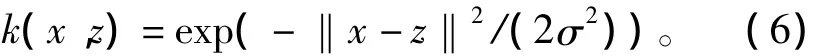
指数核函数

多项式核函数

式(6)～式(8)中，σ为高斯径向基核参数，c，d为多项式核参数。

1.2 核主元回归

核主元回归(KPCR)是在核主元分析基础上实现的，通过KPCA方法提取非线性主元，把获得的新变量作为多元自回归的自变量，进行回归计算与分析。核主元回归模型可表示为［18－19］

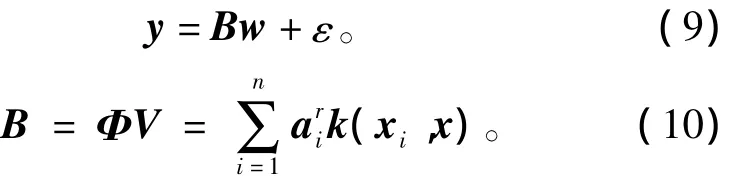
其中:ε为回归残差;w为回归系数矩阵;B为n×m维转换数据阵，转换数据阵B的详细推导求解参考文献［19］;V为m×m维特征向量矩阵，其第r列对应着特征向量vr。回归系数的最小二乘估计的计算式为

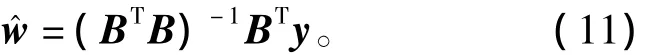
2 变压器油中气体预测MK-KPCR模型

本文提出的MK－KPCR方法是将多个不同类型的核函数进行线性加权组合，得到新的等价核，用于构建预测模型。在权衡建模精度与计算复杂度的基础上，选择两个核函数，以多项式核及高斯径向基核用于构建新的等价核。等价核函数可以表示为

其中:μj为权值，且μ1+μ2=1，0≤μj≤1，j=1，2。

为降低等价核对单个核函数参数的依赖性，提高预测建模精度，μj的选择以每个核函数预测建模的均方根误差(root mean squared error，RMSE)作为评测标准，依靠计算样本预测值和真实值之间的均方误差。对于多核问题，认为一个核函数，如果其产生小的均方误差，则它应更多地贡献合成核［10］。

RMSE定义为

权值μj的选择方法为

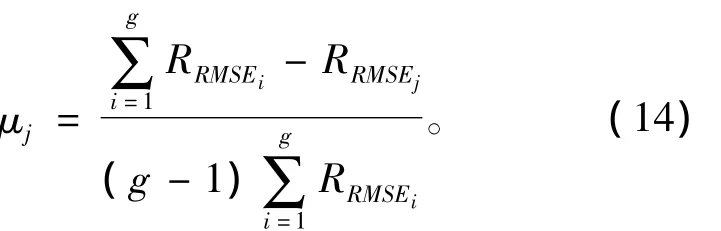
为了解决训练样本集大而出现的核矩阵计算问题，本文采用在线学习的方式，训练样本随采样时间的推移而窗式移动，即t+1时刻采集一个新样本的同时，剔除t时刻最早采集的一个旧样本，保持训练样本总数不变。选择窗口长度为n，训练样本集可以表示为

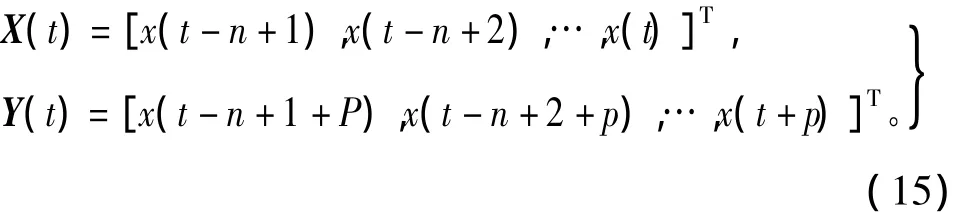
其中，x(t)=［x1(t)，x2(t)，x3(t)，x4(t)，x5(t)］为t时刻DGA 采样样本;xi(t)，i=1，2，…，5依次为氢气(H2)、甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、总烃在t时刻气体浓度采样值;p为预测步长。由于乙炔(C2H2)有时出现长连零现象，用总烃代替乙炔进行建模，总烃为甲烷，乙烷，乙烯，乙炔浓度之和。

基于MK－KPCR的建模和预测算法的步骤为

Step1:采用在线学习的方式训练采样样本，在一个新样本加入的同时，丢弃最早采集的样本，保证窗口长度n不变;

Step2:样本集Xn×m标准化处理，分别选择高斯径向基核函数和多项式核函数，按式(5)计算相应的核矩阵 K，并对核矩阵 K按式(16)作均值化处理;

式中，ln是元素为1/n的n×n常数矩阵;

Step3:解决nλa=Ka的特征值问题，并标准化ar，使λ＜ ar，ar＞ =1;

Step4:按式(10)计算转换矩阵 B，并利用式(11)计算回归系数矩阵;

Step5:利用式(17)计算训练样本的预测值;

Step6:按式(13)计算径向基核和多项式核训练样本集的均方根误差，按式(14)计算权值μj;

Step7:按式(12)构造新的等价核，按式(5)计算其相应的核矩阵K，并对核矩阵K按式(16)作均值化处理;

Step8:解决nλa=Ka的特征值问题，并标准化ar，使λ＜ ar，ar＞ =1;

Step9:按式(10)计算转换矩阵 B，并利用式(11)计算回归系数矩阵;至此，建模过程结束。

Step10:输入当前时刻检测的一个样本x(t)，标准化处理后得到的数据x(t)∈Rm，按式(18)计算对应的核矩阵kt，有

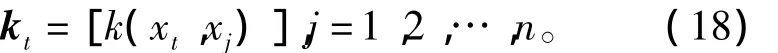
其中，xj为训练样本;

Step11:按式(19)对核矩阵kt作均值化处理;

其中，lt是元素为1/n的1×n常数矩阵;

Step12:利用式(20)计算检测样本的转换矩阵Bt;

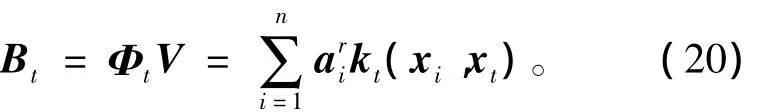
Step13:按式(21)计算当前检测样本的预测值;

Step14:令t=t+1，返回至Step1。

3 预测实例研究

本文分别采用 MGM［3］，PCR［20］，KPCR［19］和MK－KPCR算法对变压器油中溶解气体DGA样本进行一步预测和多步预测研究，即以氢气(H2)、甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、总烃这5种特征气体建模，并同时预测这5种特征气体。选取初始训练样本数50，测试10个样本的预测值。为了验证核参数的变化对KPCR和MK－KPCR建模精度的影响，KPCR中的高斯径向基核参数先后取为σ=1，σ=5和σ=10。MK－KPCR中的高斯径向基核参数与KPCR保持一致，多项式核中，核参数d=2，c在［50，100］区间内随机取值。实验数据来自2011年某变压器检测数据。

3.1 一步预测实验(p=1)

表1为MGM，PCR，KPCR和MK－KPCR模型对10个测试样本的一步预测结果，限于篇幅，表1仅给出σ=5时，KPCR和MK－KPCR模型的预测结果;一步预测误差对比结果如表2和图1所示，表2给出了测试样本集的均方根误差和各变量的均方根误差，图1给出了各样本的均方根误差。

表1 变压器油中气体浓度预测结果Table 1 Prediction of dissolved gases in transformer oil

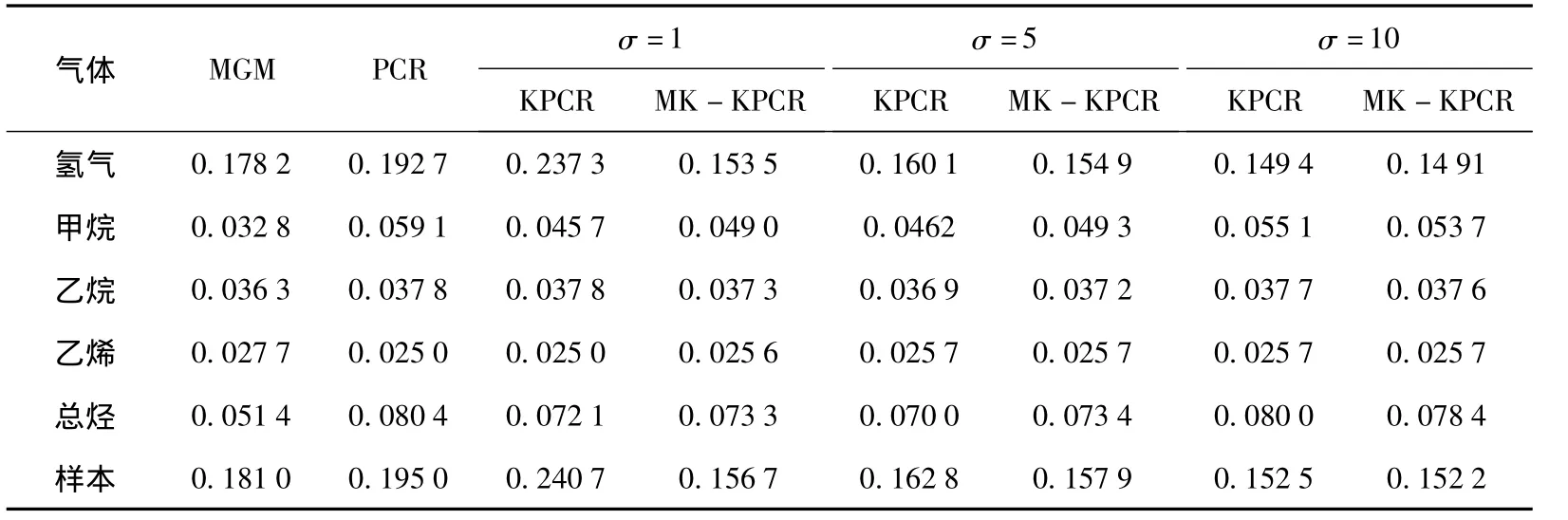
表2 变压器油中气体浓度一步预测均方根误差对比Table 2 One step prediction RMSE of dissolved gases in transformer oil

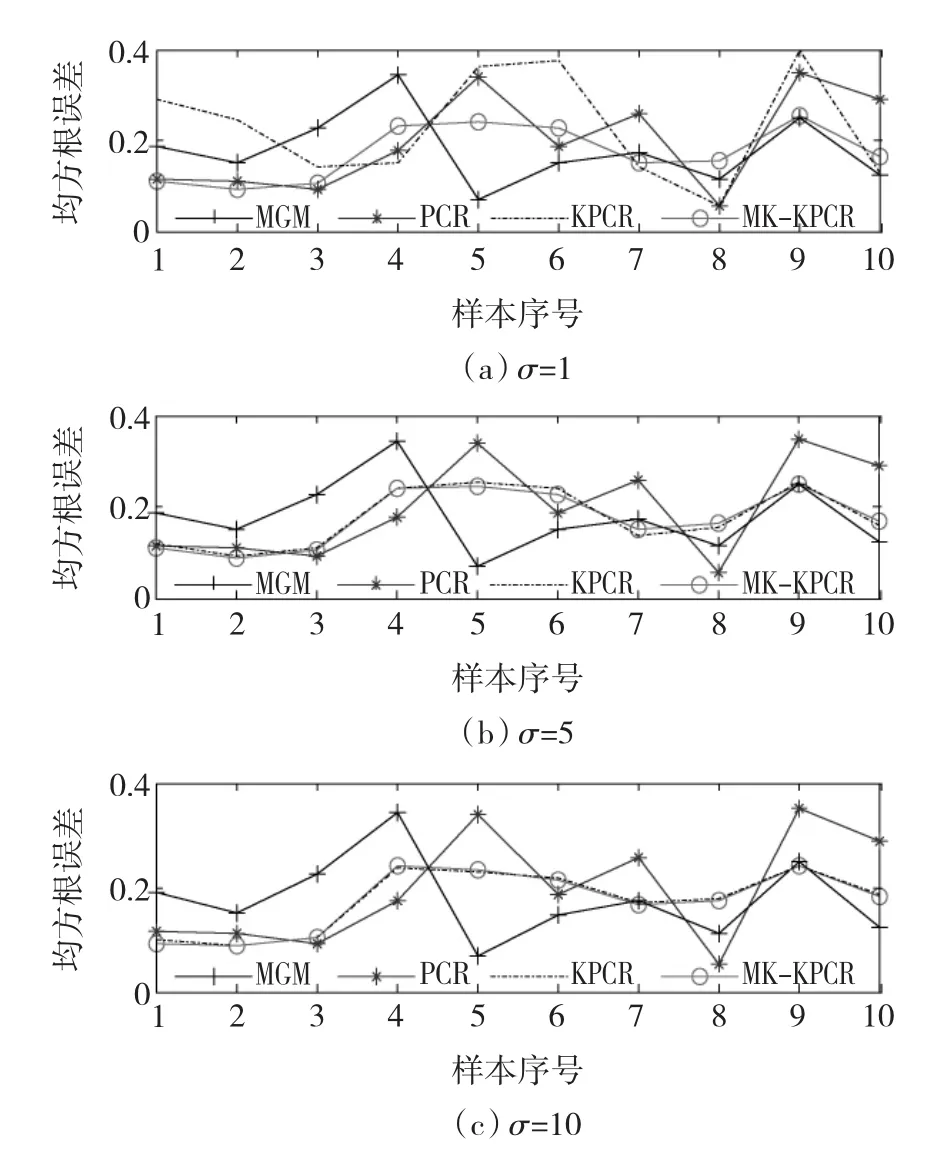
图1 各样本的一步预测误差对比Fig．1 One step prediction RMSE of samples

由表2可见，当高斯径向基核参数选择不恰当时，例如σ=1，KPCR对测试样本集的预测误差最大，为0.240 7，大于MGM和PCR;而核参数选择比较合适，如σ=5或σ=10，KPCR对样本集的预测误差分别为0.162 8和0.152 5，均优于 MGM和PCR，稍高于MK－KPCR;对于各样本的均方根误差，见图1，高斯径向基核参数选择不恰当时，如σ=1，KPCR模型的预测误差起伏较大，且样本有最大预测误差;而核参数选择比较合适，如σ=5或σ=10，KPCR模型的预测误差总体稍差于MKKPCR而优于MGM和PCR;无论σ=1，σ=5或σ=10，MK－KPCR模型的预测误差变化不大，比较稳定;由此可见，KPCR模型的预测结果依赖于核函数及参数的选择。而对比KPCR和MK－KPCR，当σ依次选为 1，5，10时，KPCR的预测误差分别为0.240 7，0.162 8，0.152 5，MK － KPCR 的预测误差分别为0.156 7，0.157 9，0.152 2，可见，高斯径向基核参数发生变化时，对KPCR算法的建模精度有较大的影响，而高斯径向基核参数的变化对MKKPCR的建模精度影响较小;无论σ=1，σ=5或σ=10，MK－KPCR方法对测试样本集的一步预测精度均优于KPCR方法，也均优于MGM和PCR。

对于样本中各变量的均方根误差，见表2，当σ=1时，KPCR对氢气的预测误差为0.237 3，远高于MGM，PCR和MK－KPCR，进而导致样本的均方误差也变差;当高斯径向基核参数选择较为恰当时，KPCR相比于PCR，对各变量的预测效果较好;对比KPCR和MK－KPCR，高斯径向基核参数发生变化时，KPCR算法对氢气的预测误差有较大的变化，而MK－KPCR对各变量的预测误差变化均较小，说明高斯径向基核参数σ对MK－KPCR的预测效果影响不大;相比于PCR，KPCR和MK－KPCR灰色预测MGM模型对乙烷的预测效果和其它方法相差不大，对甲烷和总烃的预测效果较好，对氢气和乙烯的预测效果较差，主要因为氢气和乙烯的变化趋势起伏不定，甲烷和总烃总体上呈现上升增长的趋势(见表1)，这也验证了文献［5］指出的，灰色模型的预测精度一般随数列自身规律的变化而变化，在数列有确定性趋势时预测效果较好，否则预测效果较差。

3.2 多步预测实验(p=5)

提出的MK－KPCR方法对DGA样本进行多步预测(p=5)，表3给出了10个测试样本进行多步预测(p=5)样本的均方根误差和各变量的均方根误差，图2为各样本的均方根误差。

由图2和表3可以看出，当σ=1时，KPCR对样本的预测误差为0.260 6，明显高于MGM，PCR和MK－KPCR;当高斯径向基核参数选择恰当，如σ=5或σ=10，KPCR的预测误差分别为0.161 6和0.157 4，低于MGM的0.182 3预测误差和PCR的0.1950预测误差;当σ依次选为1，5，10时，MKKPCR 的预测误差分别为0.164 9，0.159 3，0.156 7，均优于相应KPCR的预测误差，也优于 MGM和PCR;与KPCR相比，σ参数的变化对MK－KPCR的多步预测精度影响较小，采用MK－KPCR，对各样本的预测误差较为平稳，起伏不大。

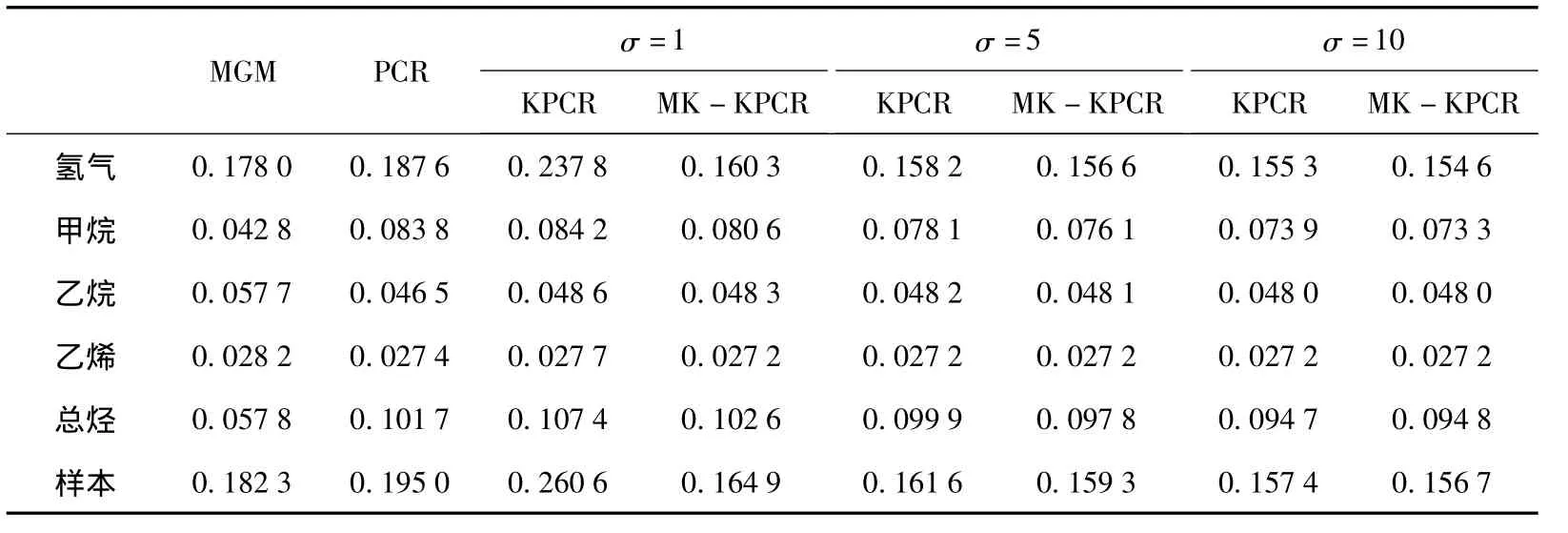
表3 变压器油中气体浓度多步预测均方根误差对比Table 3 Multiple steps prediction RMSE of dissolved gases in transformer oil

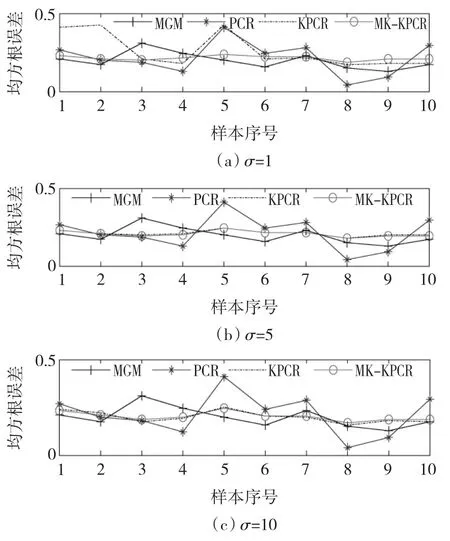
图2 各样本的多步预测误差对比Fig．2 Multiple steps prediction RMSE of samples

4 结语

提出了基于多核核主元回归MK－KPCR的变压器油中溶解气体的预测方法。采用多核学习方法，将径向基核函数和多项式核函数进行线性加权构造新的等价核，并利用窗式移动的学习方式，同时对变压器油中溶解气体进行了一步和多步预测。该方法可以看作是KPCR在多核空间中的推广。预测实验结果表明，与KPCR相比，MK－KPCR对单一核函数及其参数的依赖性较小;与灰色多变量预测模型MGM，主元回归PCR及核主元回归KPCR相比，MK－KPCR具有较高的建模精度和泛化能力。

［1］罗运柏，于萍，宋斌，等．用灰色模型预测变压器油中溶解气体的含量［J］．中国电机工程学报，2001，21(3):65 －69．

LUO Yunbai，YU Ping，SONG Bin，et al．Prediction of the gas dissolved in power transformer oil by the grey model［J］．Proceedings of the CSEE，2001，21(3):65 －69．

［2］WANG M H．Grey-extension method for incipient fault forecasting of oil-immersed power transformer［J］．Electric Power Components and Systems，2004，32(10):959 －975．

［3］肖燕彩，朱衡君，陈秀海．用灰色多变量模型预测变压器油中溶解的气体浓度［J］．电力系统自动化，2006，30(13):64 －67．

XIAO Yancai，ZHU Henjun，CHEN Xiuhai．Concentration prediction of dissolved gas－in－oil of a power transformer with the multivariable grey model［J］．Automation of Electric Power Systems，2006，30(13):64 －67．

［4］肖燕彩，朱衡君，陈秀海．用改进的灰色多变量模型预测变压器油中溶解气体的浓度［J］．电网技术，2006，30(10):86 －89．

XIAO Yancai，ZHU Henjun，CHEN Xiuhai．Prediction of gas dissolved in power transformer oil by improved multivariable grey model［J］．Power System Technology，2006，30(10):86 －89．

［5］刘思峰，郭天榜，党耀国．灰色系统理论及其应用［M］．2版．北京:科学出版社，1999．

［6］费胜巍，孙宇．用SVRM预测变压器油中溶解气体量［J］．高电压技术，2007，33(8):81 －84．

FEI Shengwei，SUN Yu．Prediction of dissolved gases content in power transformer oil by support vector regression machine ［J］．High Voltage Engineering，2007，33(8):81－84．

［7］赵石磊，张迎春．SVM回归估计方法在卫星故障诊断中的应用［J］．电机与控制学报，2008，12(4):483 －486．

ZHAO Shilei，ZHANG Yingchun．Application of SVM regression to fault diagnosis for satellite［J］．Electric Machines and Control，2008，12(4):483 －486．

［8］肖燕彩，陈秀海，朱衡君．基于最小二乘支持向量机的变压器油中气体浓度预测［J］．电网技术，2006，30(11):91－94．

XIAO Yancai，CHEN Xiuhai，ZHU Henjun．Forecasting of gas concentration in power transformer oil based on least square support vector machine［J］．Power System Technology，2006，30(11):91－94．

［9］冯磊华，桂卫华，杨锋．改进LS－SVM的直吹式制粉出力软测量建模［J］．电机与控制学报，2011，15(11):79－83．

FENG Leihua，GUI Weihua，YANG Feng．Soft sensor modeling for mill output of direct fired system based on improved least squares support vector machines［J］．Electric Machines and Control，2011，15(11):79 －83．

［10］汪洪桥，蔡艳宁，孙富春，等．多尺度核方法的自适应序列学习及应用［J］．模式识别与人工智能，2011，24(1):72－81．

WANG Hongqiao，CAI Yanning，SUN Fuchu，et al．Adaptive sequence learning and applications for multi－scale kernel method［J］．PR ＆ AI，2011，24(1):72 －81．

［11］ZIEN A，ONG C S．Multiclass multiple kernel learning［C］//Proceedings of the 24th International Conference on Machine Learning．June 20 － 24，2007，New York，USA．2007:1191－1198．

［12］张军峰，胡寿松．多重核学习非线性时间序列故障预报［J］．控制理论与应用，2008，25(6):1142 －1144．

ZHANG Junfeng，HU Shousong．Nonlinear time series fault prediction by multiple kernel－learning［J］．Control Theory＆ Applications，2008，25(6):1142 －1144．

［13］陈强，任雪梅．基于多核最小二乘支持向量机的永磁同步电机混沌建模及其实时在线预测［J］．物理学报，2010，59(4):2310－2318．

CHEN Qiang，REN Xuemei．Chaos modeling and real－ time online prediction of permanent magnet synchronous motor based on multiple kernel least squares support vector machine［J］．Acta Physica Sinica，2010，59(4):2310－2318．

［14］许洁，胡寿松．基于KPCA和MKL－SVM的非线性过程监控与故障诊断［J］．仪器仪表学报，2010，31(11):2428 －2433．

XU Jie，HU Shouson．Nonlinear process monitoring and fault diagnosis based on KPCA and MKL － SVM［J］．Chinese Journal of Scientific Instrument，2010，31(11):2428 －2433．

［15］LEE J M，YOO C，CHOI S W，et al．Non－linear process monitoring using kernel principal component analysis［J］．Chemical Engineering Science，2004，59(1):223 －234．

［16］齐咏生，王普，高学金，等．改进MKPCA方法及其在发酵过程监控中的应用［J］．仪器仪表学报，2009，30(12):2530－2538．

QI Yongsheng，WANG Pu，GAO Xuejin，et al．Application of an improved multi－way kernel principal component analysis method in fermentation process monitoring［J］．Chinese Journal of Scientific Instrument，2009，30(12):2530 －2538．

［17］CHOI S W，LEE C，LEE J M，et al．Fault detection and identification of nonlinear processes based on kernel PCA［J］．Chemometrics and Intelligent Laboratory Systems，2005，75(1):55－67．

［18］张曦，陈世和，朱亚清，等．基于KPCR的发电机组参数预测与估计［J］．电力自动化设备，2010，30(10):54 －57．

ZHANG Xi，CHEN Shihe，ZHU Yaqing，et al．Parameter prediction and estimation for turbine generator based on KPCR［J］．Electric Power Automation Equipment，2010，30(10):54 －57．

［19］ZHANG Xi，MA Sile，YAN Weiwu，et al．A novel systematic method of quality monitoring and prediction based on FDA and kernel regression［J］．Chinese Journal of Chemical Engineering，2009，17(3):427 －436．

［20］贺湘宇，何清华，郭勇，等．基于主元回归模型的挖掘机液压系统故障诊断［J］．江苏大学学报:自然科学版，2008，29(2):106－109．

HE Xiangyu，HE Qinghua，GUO Yong，et al．Fault diagnosis for excavator’s hydraulic system based on principal component regression mode［J］．Journal of Jiangsu University:Natural Science Edition，2010，30(10):54－57．