针对Swarm 模型突现行为的新的动力学指标研究

王 利

(重庆邮电大学计算机学院，重庆 400065)

0 引言

突现又称“涌现”(emergence)是多Agent系统的一个基本特征，概括地讲就是系统内的若干个体，按照某种方式发挥系统作用的同时，会产生出整体具有而各个体不具有的新的特性［1］。美国生物学家摩尔根在1923年出版的《突现的演化》一书中指出:“宇宙在进化的每一阶段上都有新的性质、新的事物突然地、神秘般地被创造出来［2］。”系统功能之所以往往表现为整体大于部分之和，就是因为系统突现了新质的缘故。

自然界中迁徙的鸟、成群的鱼、群居的蚂蚁和蜜蜂都是Swarm的典型例子，Swarm模型中的个体被称为agent，每个agent遵守简单的规则进行运动，从而产生出新的特性或特质，而很多学者认为这种突现行为在一定程度上是可以被认知的。从相关Swarm模型突现行为研究文献可知，吴渝［3］等学者从该角度提出基于动力学参数等属性的定量分析方法，也借鉴了复杂网络学中的聚类指标、信息论中的信息熵以及系统动力学中内部能量等指标来对Swarm模型中的突现行为进行定量分析和研究［4］。这些方法一是计算相对复杂，二是对突现行为的分析和研究并不直观。

所以，本文直接从Swarm模型中个体的运动状态出发，借鉴物理学中的伊辛模型，选取简单直观的2个动力学指标，对Swarm模型产生的突现行为进行解释、观测和分析，从而更好地了解其运动规律及参数的意义。

1 Swarm突现计算模型

L.Spector和J.Klein根据Craig Reynolds提出的“Boids”模型理论［5］，给出了相关行为的具体计算方法［6］，Swarm模型中Agent的瞬时加速度向量的计算公式如下:

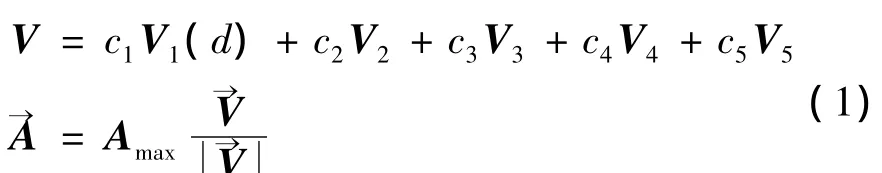
(1)式中:常量c1－c5为向量V1到V5的权值;d是某一智能体与它周围的智能体应保持的距离值;V1是某一智能体指向远离其自身范围d内的所有智能体的均向量;V2是指向模拟世界中心的向量，由模拟世界的中心决定;V3是某一智能体周围所有智能体的平均速度向量;V4是某一智能体指向其周围所有智能体所构成的中心的向量;V5是一个随机单位长度向量;→V是所有向量的加权和向量;→A是在每一个模拟时间段中所产生的智能体瞬时加速度向量(＜Amax);Amax和Vmax分别是智能体可达到的最大加速度和最大速度。

在前期工作中，我们在 Matlab7.1环境下对Swarm模型进行仿真实验，通过给c1－c5，Vmax，Amax和d这几个模型参数设置不同的值，我们得到的形状分别有:零散型、群聚型、圆圈型和直线型。其中，零散型为无突现行为，而其他3种形状都为突现行为，Matlab平台下的仿真结果截图如图1所示。

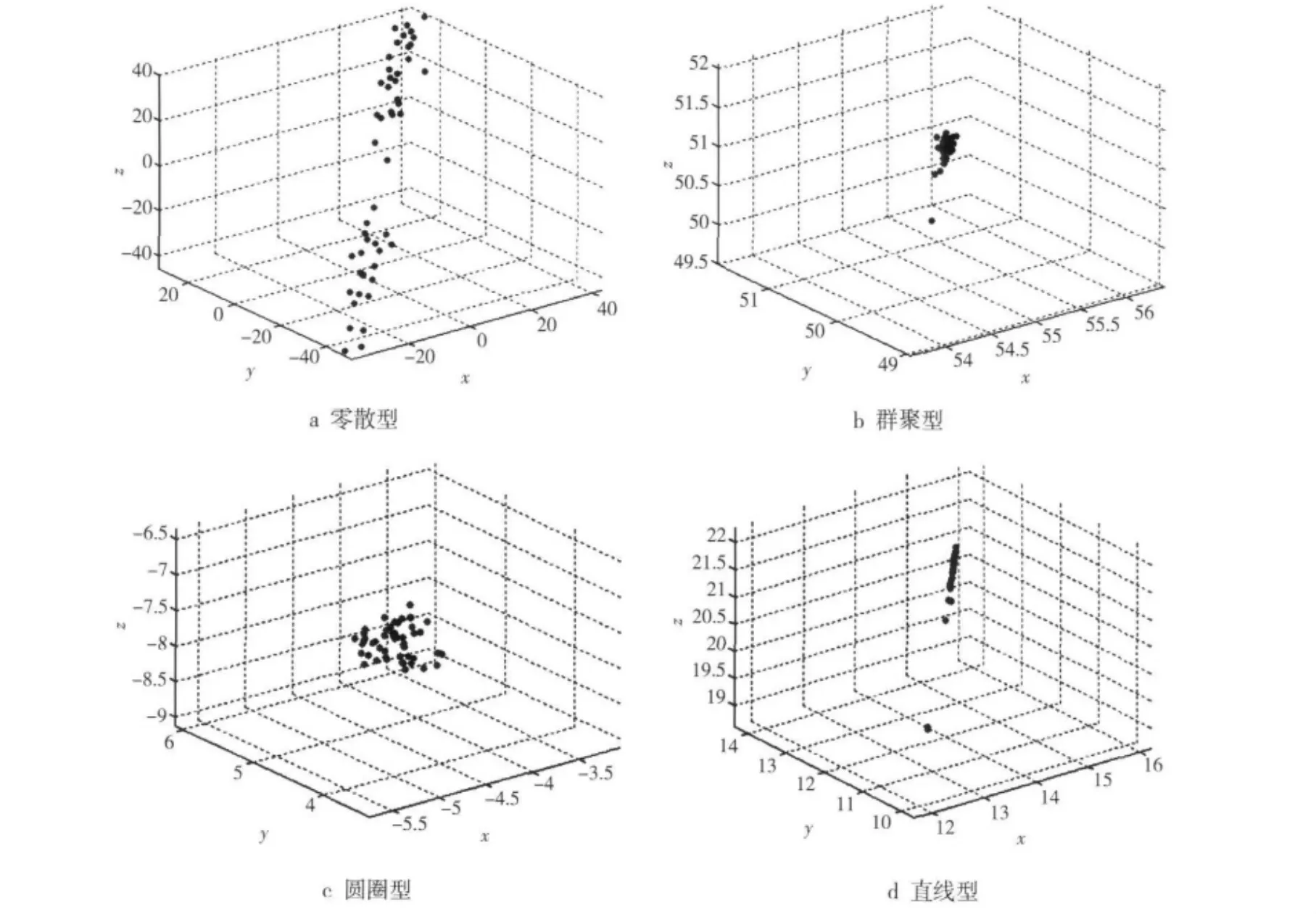
图1 不同形状的仿真结果Fig.1 Simulation results of different shapes

2 动力学指标选取依据

2.1 平均速度Vt

伊辛模型是物理学家恩斯特·伊辛［7］于1925年提出的，伊辛模型是一个非常简单的模型，在一维、二维或三维的每个格点上占据一个自旋，每个自旋在空间有2个量子化的方向，在绝对零度时，所有自旋的取向完全一致，有2个可能，都是向上或都是向下，一旦选定了向上，就大家一起向上，非常有序，单个自旋的微小磁场加到一起，便会形成一个很强的磁场，铁块就成了磁体［8］。Swarm模型中每个agent的运动类似于磁铁中的每个自旋，只是agent运动的方向不在局限于上下2个方向，当agent运动的方向大多数一致时，大多数个体处于有序状态，所有agent的运动速度之和就会比较大，Swarm模型产生突现行为;当agent的运动方向比较纷乱时，大多数个体处于无序状态，所有agent的运动速度相互抵消，运动速度之和会相对较小，模型产生无突现行为。在这里agent的运动速度之和就好比磁铁的磁化强度，当运动速度之和比较大时，表明大多个体运动是有方向性的、一致的，当运动速度之和小时，表明大多个体运动是无序的。在本文中讨论的所有agent速度之和是三维的、有方向的，无法判断其大小，所以，选择每个时刻所有个体的平均速度来对Swarm模型产生的突现行为进行分析，在Swarm模型中平均速度的计算公式如(2)式:

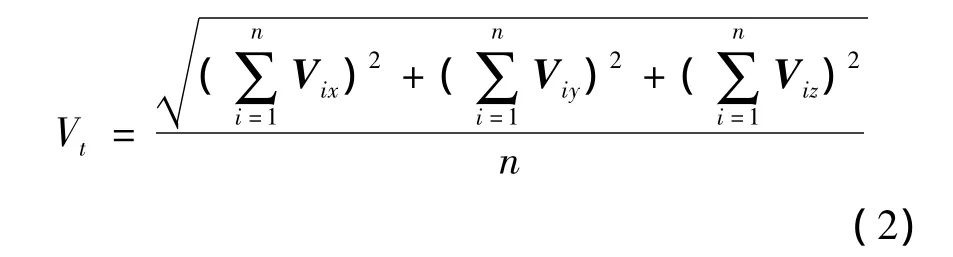
(2)式中:Vt为t时刻的平均速度;n为个体总个数;Vix，Viy和Viz分别为个体i在t时刻的x轴、y轴和z轴方向的速度。

2.2 随机速度c5V5

在伊辛模型中当温度足够热时，温度将会对有序的状态进行扰动，某一个自旋可能会挣脱其他自旋对它的相互作用的束缚，而改变自旋方向，这个调皮的自旋可能又会影响其他自旋的取向，从而将它们自旋的有序方向搅乱，弄得它们的指向无规律起来，各个原子的微小磁场彼此抵消掉，铁块就成了非磁体［8］。在Swarm模型中V1－V4描述的都是个体周围邻居及模拟中心对个体的影响，V5描述的是随机单位长度，c5V5构成了随机速度，随机速度是外界对Swarm模型的影响，类似于温度对铁块的影响，当随机速度比较大时，Swarm模型产生无突现行为，在本文中通过实验验证了这个结论的正确性。

下面通过实验来对这2个指标进行分析和验证。

3 实验设置及分析

3.1 实验设置

下面的实验中所选取的模型参数根据表1中的参数范围设定(表1中的数据来自文献［3］)，分别针对群聚型、零散型、圆圈型和直线型4种情况进行实验，每种情况各50组参数，每次实验使30个个体运行3 000 s。

表1 对应群体行为中各参数取值关系表Tab.1 Rules of parameter values in different behaviors

3.2 实验结果及分析

1)平均速度:用公式(2)计算每个时刻的平均速度。图2给出了平均速度随时间变化曲线。

a)实验结果。在图2中，横坐标表示时间t，单位为s，纵坐标表示平均速度v，平均速度的单位和Swarm模型参数初始值的单位设置息息相关，在这里单位可以认为是步长数/s，在不同的应用环境中步长数可以是m，cm或mm等为单位，图2中圆圈处表明突现产生的时刻。

b)实验分析。由于零散型中个体运动的方向是不一致的、纷乱的，所以图2a中平均速度的变化是无规律的。对于群聚型、圆圈型和直线型，当突现产生后大多数个体都紧密聚在一起，运动方向非常一致，从图2b－d中可以看出，刚开始平均速度曲线处于无规律波动阶段，Swarm模型处于无突现状态;随着突现时刻的来临，曲线逐渐上升并稳定在某一个范围内，这个范围值和Swarm模型参数的初始值设置息息相关;最后曲线保持近似直线或上下波动某一固定形状变化，这时Swarm模型保持稳定的突现状态。图2c中，由于模型在突现产生一段时间后按圆圈型运动，所以，平均速度曲线上下波动。上面的实验结果和Swarm模型的实际运动轨迹一致，说明用平均速度可以很好地反映出Swarm模型的运动规律以及突现产生的时刻。

图2 平均速度随时间变化图Fig.2 Changes of the average velocity with time

2)随机速度c5V5:在测试随机速度c5V5对Swarm模型的影响实验中，使c1～c4，Vmax，Amax和d的值保持不变，由于V5是随机单位长度，所以只需使c5的值不断变化。

a)实验示例。当 c1～ c4，Vmax，Amax和d的值分别设置为 4.0，10.0，8.0，7.0，9.0，40.0，0.01，c5的值为1～8.0时，实验结果为群聚型如图3a所示;c5值为9.0～15.0时，实验结果为轻度零散型如图3b所示;c5为16以上时，实验结果为零散型如图3c所示。

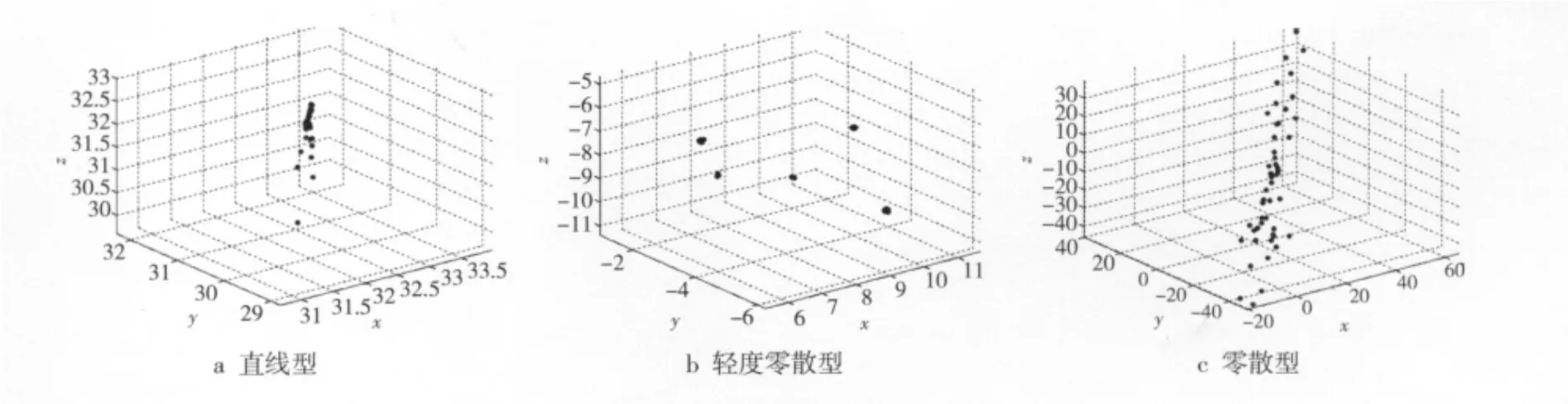
图3 实验运行结果Fig.3 Experiment results

b)在此实验中我们只讨论了模型参数值大于0的情况，通过群聚型、直线型、圆圈型和零散型每种情况各50组实验，可以得出表2所示的结论。和d取表1中的任意值，而c5的值在16±以上时，模型运动结果都为零散型，而当模型参数c1～c4，Vmax，Amax和d不取表1中的值，则c5不符合表2的结论，由此可以看到，表2的结论和模型参数的初始值密切相关。可以肯定地说，当c5的值足够大时，模型运动结果肯定为零散型(无突现)，和伊辛模型中温度类似(随着温度的升高，铁块的磁性消失)。当采用Swarm模型对实际问题进行模拟仿真时，我们可以根据需要来合理地设置c5的值。

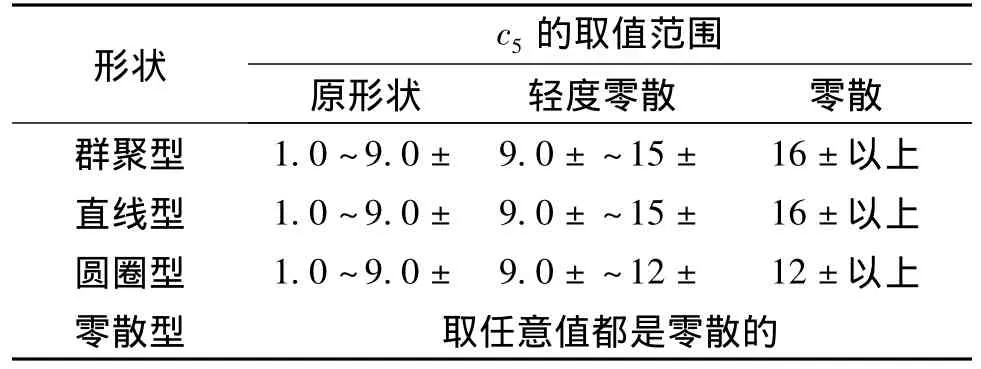
表2 c5取值范围与运动型状的关系表Tab.2 Values of c5parameter in different behaviors

4 总结

可以得出结论:当模型参数 c1～c4，Vmax，Amax突现是一种常见的自然现象，在生物学、物理学、经济学等社会学科中都存在着大量的突现现象。由于Swarm模型的简单实用，已经有很多学者采用Swarm模型对股票市场、疾病传播、虚拟社区的形成、网络舆论等突现现象进行模拟及预测。本文用平均速度和随机速度对Swarm模型进行分析及研究，从而更加深入地了解Swarm模型的运动规律及参数属性，能更好地在实际中应用。

［1］李润珍，武杰，程守华.突现、分层与对称性破缺［J］.系统科学学报，2008，16(2):9-13.LI Run-zhen，WU Jie，CHENG Shou-hua.Emergence，hierarchy and symmetry breaking［J］.Journal of Systems Science，2008，16(2):9-13.

［2］SPERRY R W.Neurology and the Mind-Brain Problem［M］.American:American Science，1952:295-295.

［3］WU Yu，ZHOU Kai，SU Jie，et al.Kinetic parameter mining of swarm behavior based on rough set［J］.Communications of SIWN，2008，4(1):64-69.

［4］吴渝，周凯，李银国.Swarm突现行为的定量评估指标［J］.控制理论与应用，2010，27(8):1086-1092.WU Yu，ZHOU Kai，LI Yin-guo.The Evaluation Metrics for Swarm Emergent Behaviors［J］.Control Theory and Applications，2010，27(8):1086-1092.

［5］REYNOLDS C.Flocks，Herds，and Schools:A Distributed Behavioral Model［J］.Computer Graphics，1987，21(1):25-34.

［6］SPECTOR L，KLEIN J.Evolutionary Dynamics Discovered via Visualization in the Breve Simulation Environment［C］//Proceedings of 8th International Conference on the Simulation and Synthesis of Living Systems，Artificial Life VIII.Boston:MIT press，2002:163-170.

［7］ISING E.Eeitrag zur theorie des ferromagnetismus［J］.Z Phys，1925，31:253-258.

［8］张志东.伊辛模型的研究进展简介［J］.自然杂志，2008，30(2):94-98.ZHANG Zhi-dong.Advances on the Ising Model［J］.Nature magazine，2008，30(2):94-98.