一种用于MEMS 动态测量的最优盒计数分形维数算法

罗 元，蒋秋照，张 毅

(重庆邮电大学光纤通信技术重点实验室，重庆 400065)

0 引言

微机电系统(micro electromechanical system，MEMS)的动态特性决定了MEMS器件的基本性能，其测试得到了国内外的高度重视，在众多方法中基于微视觉的技术因能实现高速高精度测量而备受关注，分形因具有自相似这一重要特征在充分利用图像相关性方面独具潜力。但分形理论在MEMS测试中目前基本都用于表面形貌的分析，获得的是MEMS表面形貌特征和分形维数之间的关系［1-2］，很少有人将分形理论用于MEMS动态测量中。研究面内位移前后采集的数字散斑图像的分形性质，通过分形相关法、分形插值法实现位移的测量;分形图像边缘和分形特性曲线之间有互映射关系，通过提取MEMS位移或旋转时动态图像序列的边缘，对图像边缘的分形性质与旋转角度［3］的关系进行研究，实现基于分形的角度定位;再对离面位移与角度的关系进行研究，完成基于分形理论的离面位移测量。所以有效的分形维数算法是实现采用分形维数描述分形特征的一个前提条件。而计盒维数法由于其计算简单易懂，得到了广泛的应用。在计盒维数法中差分盒计算(difference box counting，DBC)法又是目前计算维数的最常用的方法。本文通过对差分盒计数法存在“空盒子”的缺陷的分析，从而在最小盒计数法［4］的基础上提出了一种对“空盒子”不予计数的最优盒计数分形维数算法。并用实验验证了该算法的有效性，以便于MEMS动态测量的后续研究。

1 差分盒计数法

1.1 分形维数的一般形式

分形维数［5］是分形几何描述分形特征的基本参数，计算分形维数的方法有很多，如点像素覆盖法［6］、毯子法［7］、计盒维数法［7］等。计算分形维数的一般形式［5］为

(1)式中:ε是小立方体一边的长度;N(ε)是覆盖被测形体所需小立方体的总数。计盒维数是一种被广泛应用的分形维数，在分形理论应用研究中提出的许多维数的概念都是计盒维数的变形。

1.2 差分盒计数法

差分盒计数法［7-8］是计盒维数方法中较优的方法，也是目前广泛运用的维数计算法。它将图像(见图1)想象成三维空间中的曲面［9］z=f(x，y)，其中x，y表示平面位置，z轴表示该位置对应于图像像素的灰度值。设图像大小为M×K，灰度级为H，xy平面被分割成许多大小为r×r的网格，每个网格对应于三维空间中的一叠r×r×r大小的盒子;设在第(i，j)个网格中，图像灰度的最大值位于第l个盒子内，最小值位于第m个盒子内，则

(2)式中，nr是覆盖第(i，j)网格中的图像所需的盒子数，而覆盖整个图像的盒子数Nr为

不同的r，Nr也不同，对得到的序列(lnr，lnNr)，在双对数坐标中对数据点 (lnr，lnNr)进行直线拟合［6-7］，所得直线斜率的绝对值即分形维数D。

图1 DBC法示意图Fig.1 Schematic diagram of DBC

按照盒维数估计的定义，不同尺度r下的Nr为覆盖分形的最少盒子数，表明的含义［9］是:①完全覆盖分形的盒子总数为Nr;②Nr在数量上最少。③所有的盒子都是非空的。然而，差分盒计数法在估计图像的分形维数时，只能保证Nr个盒子完全覆盖分形，并不能确保盒子数Nr是最少的，如果灰度曲面发生了剧烈变化(见图2)，第2、第3或第4个盒子都可能是“空盒子”(盒子中没有包含灰度曲面上的点)。由于“空盒子”出现在2个点的中间位置，这时按差分盒计数法得到的覆盖灰度曲面的nr(i，j)盒子中，必然包括“空盒子”。如果图像灰度曲面变化较剧烈，盒子较小，就很容易出现“空盒子”，因此按差分盒计数法估计覆盖图像灰度曲面的盒子数是不准确的，导致维数偏大。为了克服差分盒计数法的缺点，本文在最小盒计数的基础上提出了一种能更好估算图像分形维数的算法，最优盒计数法(optimal box counting method，OBC)。

图2 DBC法中出现“空盒子”示意图Fig.2 A diagram of DBC which exists empty boxes

2 最优盒计数法

最优盒计数法对平面网格的划分仍采用差分盒计数法的划分方式，只是对那些覆盖图像灰度曲面的“空盒子”不予计数，以便能准确求取覆盖分形曲面的最少盒子数。具体实现过程如下。

在图2中，设图像大小为M ×N，将x－y图像平面分成大小为r×r的网格，每个网格对应于三维空间中的一叠r×r×r的正方体盒子，考虑第(i，j)个平面网格，第(i，j)个格子共对应图像灰度曲面上K=(r+1)2个点，设这些点组成的集合为Zij={f1，f2，f3，…，fK}。对集合 Zij中的每个元素 fi(i=1，2，…，K)，若

(4)式中，fix()是一个函数，它对一个实数执行舍弃小数部分取整数部分的操作，并返回该实数的整数部分，则可以确定点fi位于第S个盒子中，从而得到集合S，即

(5)式中，集合S为覆盖点集Zij的所有盒子的编号集合。对集合S，凡是在集合S中只出现1次的元素，全部保留;凡是在集合S中只出现2次或2次以上的元素，只保留1个。这样就得到一个新的盒子编号集合S'，即

设Q为集合S'中的元素个数，则意味着在第(i，j)个网格中，覆盖图像曲面的盒子数为

对得到的序列(lnr，lnNr)，用最小二乘法计算(lnr，lnNr)的斜率，则斜率的绝对值就是图像的分形维数。

3 实验结果及分析

本文用Sierpinski三角毯(见图3)和Sierpinski正方毯(见图4)图形进行实验。首先将图像进行预处理，二值化得到M×N的数据矩阵，将矩阵划分为边长为r(最小为一个像素)的盒子，用DBC和OBC两种方法计算整个矩阵中所占据的盒子数Nr，然后改变盒子的边长r2，r3，…，计算出相应的盒子总数Nr，并绘制在坐标系中;利用最小二乘法对这些点进行线性拟合，所得的直线斜率的绝对值就是图像的分形维数，2种方法的程序流程如图5所示。

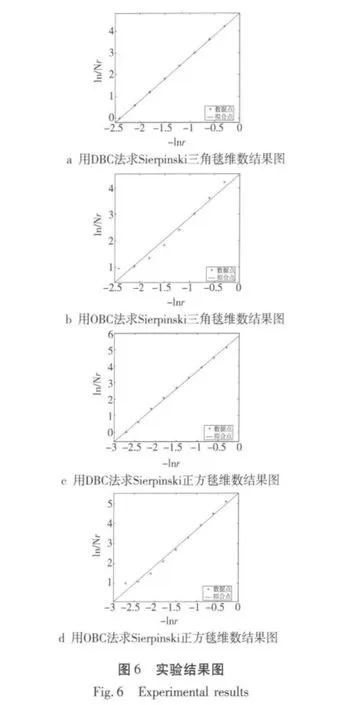
根据MATLAB图像处理功能和两种维数计算的方法对Sierpinski三角毯和正方毯进行维数计算，然后编写程序得到仿真图，如图6所示，横坐标是不同尺度r的负对数，纵坐标表示对应尺度r下的覆盖分形曲面的总盒子数的对数值，用最小二乘法拟合后，直线的斜率就是分形的维数。

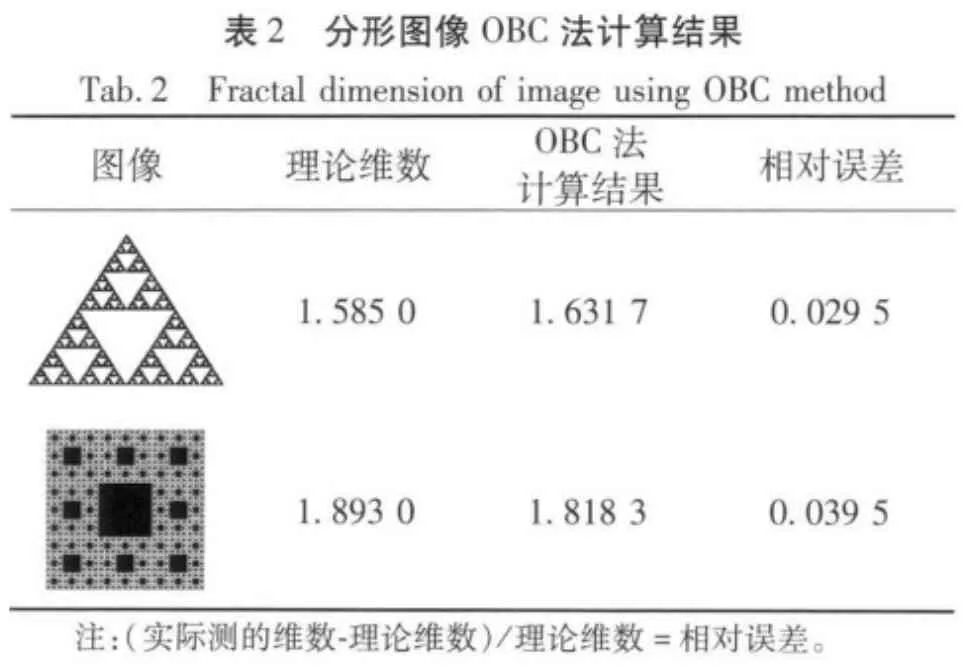
实验所得的维数和与理论维数的相对误差见表1和表2，表1是DBC法和像素点覆盖法的维数计算结果，表2是OBC法的维数计算结果。

?

图6a和图6c图是DBC法的实验结果图，直线的斜率表示分形维数，因为没考虑“空盒子”，所以直线拟合的较好，对应尺度下的数据点和拟合点相差不大。图6b和图6d是采用OBC法的仿真结果图，它去除了“空盒子”，并且在不同的尺度下出现“空盒子”数不同，尺度越小出现“空盒子”越有可能且越多，得到的数据点就比较没规律，有的偏离拟合点会比较远，所以直线拟合得不是很好，但直线的斜率更能准确地反映图像的分形维数。而表1和表2计算的维数值和相对误差也证明了OBC法比较优越。对分形图像分维数的计算具有普适性。因而将其应用在基于分形理论的MEMS动态测量中会使得测量更加准确。

4 结束语

本文提出了一种基于最小盒计数法的最优盒计数分形维数算法。从理论出发分析了该算法的优点:克服了差分盒计数法在计算盒子数时存在“空盒子”的缺陷。并通过用MATLAB软件进行仿真验证，结果表明该算法是有效的。以便将该算法运用在MEMS的动态测量中，实现基于分形的位移测试和角度定位。

［1］LUO Yuan，ZHANG Yi，XU Xiao-dong.Topography of micromirror for metal MEMS optical switch based on fractal theory［C］//Proceedings-Spie the International Society for Optical Engineering.USA:International Society for Optical Engineering ，2007(6724):672-675.

［2］XIONG Xiang，ZHOU Yan，ZHU Jian-xin.Fractal Analysis of the wear in Micro-electro-mechanical Systems(MEMS)［J］.Lubrication Engineering.2008，33(6):675-679.

［3］胡晓东，李晓俊.微结构平面旋转运动角度测量的研究［D］.天津:天津大学，2007:49-67.HU Xiao-dong，LI Xiao-jun.Study on Angle Measurement about In-plane Rotation Motion in MEMS［D］.Tianjin:Tianjin Universy，2007:49-67.

［4］WEI Gang，TANG Ju.Study of Minimum Box Counting Method for image fractal dimension estimation［C］//Proc of IEEE International conference on Electricity Distribution.［s.l.］:IEEE Press，2008:1-5.

［5］KHOURY Marc，WENGE Rephael.On the Fractal Dimension of Isosurfaces［J］.IEEE Transactions on Visualization and Computer Graphics，2010，16(6):1198-1205.

［6］林道云.掺用沸石岩矿粉建筑砂浆的力学性能及其抗压断面的分形定量表征［D］.广州:华南理工大学，2010.LIN Dao-yun.Rock and Mineral Powder Mixed with Zeolite Building Mortar and Compressive Mechanical Properties of Cross-section of the Quantitative Characteriz-ation of the Fractal［D］.Guangzhou:South China University of Technology，2010.

［7］赵玲.基于图像的多孔材料特征分析与物性测量研究［D］.武汉:武汉理工大学，2010.ZHAO Ling.Image-based Porous Materials Characterization and Measurement of Physical Properties［D］.Wuhan:Wuhan University of Technology，2010.

［8］IVANOVICI Mihai，RICHARD Noël.Fractal Dimension of Color Fractal Images［J］.IEEE Transactions on image processing.2011，20(1):227-235.

［9］尹贤龙.基于图像分形维数估计的最小盒计数法的研究［J］.电气应用，2006，25(9):93-97 YIN Xian-long.The Study on the Minimum Box Counting Algorithm Based on Fractal Dimension［J］.Electrotechnical Application，2006，25(9):93-97.