一类欠驱动系统的频域反步法设计

何朕， 王广雄， 杨文哲

(哈尔滨工业大学控制科学与工程系，黑龙江哈尔滨 150001)

0 引言

欠驱动系统是指系统的控制输入的个数m少于自由度数目n，即m＜n。在生产和科研活动中有不少的机械系统和运动系统都是欠驱动系统。对于用运动学模型来描述的欠驱动系统，例如轮式机器人，系统的主要问题是具有不可积分的运动学(或速率)约束，称为非完整控制［1］，非完整系统的镇定需要用不连续或不光滑的反馈控制律。对于具有动能T的动力学系统，其运动问题可通过Lagrange方程来进行描述，欠驱动动力学系统也可能存在类似的约束，即不可积分的动力学(或加速度)约束［2-3］，也是不能用光滑的控制律来进行镇定的。不过有相当一部分的欠驱动动力学系统并不存在不可积分的约束，这些系统就可以用光滑的控制器。即使是具有不可积分约束的欠驱动系统，如果只研究其跟踪控制问题，也可以采用连续控制律［4-7］。对于这些可以采用连续控制律的系统来说，常规的控制设计方法原则上都是可以用的，较为系统性的有Ortega的对互联结构与阻尼进行配置的无源性控制(interconnection and damping assignment-passivity based control，IDA-PBC)［8-9］。不过这种无源性IDA-PBC的偏微分方程一般是很难处理的，而且IDA-PBC法一般只谈稳定性，并不包含控制系统设计中的性能(performance)内容。与IDA-PBC法平行的各种非线性(状态空间)方法原则上也都可以用来对欠驱动系统进行设计，例如输入输出精确线性化方法［10］，Kokotovi c＇的反步法 (backstepping)［11-12］和 H∞扰动抑制控制［13-15］等方法，其中反步法设计也是一种系统性的设计方法，并且得到广泛的认同。

对于欠驱动动力学系统来说，根据其广义坐标之间的相互关系还可分为有动态联系和无动态联系的系统。有动态联系的系统又称为有耦合的系统，例如对垂直起降飞机来说，滚动力矩和横向加速度之间是有耦合的［5］。对于有耦合的系统来说，如果采用反步法来设计，就需要通过坐标变换和输入变换，先将其解耦并变换成严格反馈系统，再采用反步法［3-5］。不过这种有耦合的系统的设计一般还是比较容易处理的。因为在这种系统中，即使是被动的自由度，也还可以通过耦合项与控制输入建立联系。相比之下，无动态联系的欠驱动系统的控制设计就有一定的难度。因为无动态联系的欠驱动系统只能通过广义坐标建立起联系，如果系统处于稳定状态，广义坐标等于零，这时系统中的被动自由度与控制输入的联系就中断了。所以从控制的角度来说，无动态联系的欠驱动系统的控制设计的难度就会更大一些。本文以无动态联系的欠驱动动力学系统作为欠驱动系统的代表来进行研究，这样更能反映出本文所提出的设计方法的特点。

从反步法来说，标准的反步法是一种状态空间方法［12］，是先从一个可镇定的子系统(一般是一个一阶的子系统)开始，设计一反馈控制律。由于该子系统的实际输入量并不是设计时用的这个虚拟输入，二者是有误差的，所以要再在该子系统前加一积分环节来消除误差，这样逐级递推设计直到所要加的虚拟输入是真正的控制输入 u［4，11，16］。这样逐级递推可得到Lyapunov函数的一个递推公式，根据该Lyapunov函数的导数要小于零的条件，算得所要求的控制律u。不过这种状态空间反步法也存在着一些问题。第一个问题是控制律中的求导运算。因为反步法处理的系统一般都包含不确定性，有的是非线性与未知参数相乘而形成的参数不确定性，有些非线性项则仅知其摄动的界，而设计要求系统的Lyapunov函数的导数要小于零，即V·＜0。根据这个不等式来求解的控制律中就会出现导数项，包括对一些非线性函数的求导。反步法中一步接一步的递推运算，会使求导运算的项目迅速增加，大量的求导运算成为反步法应用时的一个累赘［3，17-18］。常规反步法的第二个问题是设计实现时往往是一个单回路系统［11，18］。由于是单回路系统，鲁棒性差，容易受到参数摄动和各种扰动的影响，所以反步法设计常还要另外附加一些鲁棒性和自适应的设计考虑［11-12］。另外，反步法中还要求这些摄动能用有界算子来描述，如果有相乘的非线性项，例如x1x24，就满足不了这一要求［11-12］。针对上述反步法中的问题，本文提出一种新的反步法设计思路，可以避免或至少可以改善上述的这些问题，这就是频域反步法。

1 频域反步法设计

本文的反步法设计不是一个积分环节一个积分环节的往前推进，而是根据可测到的物理变量，一个回路一个回路的往前推进。具体来说是，先从一个可镇定的子系统开始，设计一输出反馈(虚拟的)。再根据对象本身的构成往前推，设计第二个反馈回路来消除实际变量与这个虚拟输入变量之间的误差。这样逐级递推直到所要求的控制量是真正的控制输入u。由于是一个回路一个回路的递推进行，一般系统也就只有2、3个回路，所以系统的实现比较简单。这里设所讨论的系统的非线性状态方程中的各函数向量都是光滑的，即系统在平衡点是可线性化的，所以可以先按线性化系统来设计，再分析其吸引域或稳定区域。这种反步法从第二步开始，系统的复杂度就增加了。因此作为一种系统性的方法来说，宜采用H∞控制来进行设计，即设计每一步的输出反馈下的H∞控制律。这个H∞优化求解与常规的反步法中递推求解Lyapunov函数所起到的作用是相同的，是为了求得保证稳定的最终的控制律。H∞控制理论是一种频域设计(指设计指标和设计考虑都是从频域上来提出的)和状态空间计算相结合的控制系统的设计理论［19］。因此，相对于状态空间反步法来说，本文的反步法可称为频域反步法。由于H∞设计中可包含鲁棒性要求，而且所设计的系统是由多重反馈回路所构成的，所以频域反步法比单回路的状态空间反步法具有更强的鲁棒性。不必要像状态空间反步法那样，每一步都要另外附加自适应或鲁棒性的考虑。

现结合一球-杆系统来进行说明。图1为球-杆系统的示意图［8，11，20］。图中 τ为施加在杆上的力矩，α为杆的转角，x为球在杆上的位置。这个球的位置x不是直接可控的，x是通过杆的转动来控制的。之所以举球-杆系统为例，是因为球-杆系统是这类无动态联系的欠驱动动力学系统的典型系统。其非线性微分方程中就含有前面所说的变量相乘的非线性项+。这里+号表示正反馈，x1为小球的位置，x4为杆转动的速率。从物理概念上来说，就是当偏差较大时，转动中所产生的离心力会将杆上的小球甩出去。这种非线性项不能用有界算子来描述，所以球-杆系统包含了这类系统的设计难点，也经常是一些新的系统设计方法在提出时的研究对象［8，10，11］。

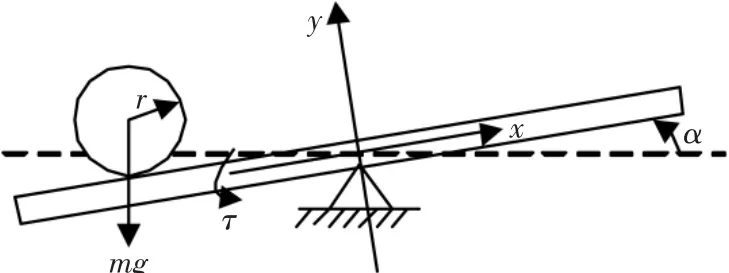
图1 球－杆系统Fig．1 The ball and beam system

本例的背景是德国Amira公司生产的BW500球-杆系统，球的转动惯量Ib=4.32×10-5kg·m2，球的质量m=0.27 kg，球的半径r=0.02 m，杆的转动惯量Iq=0.140 2 kg·m2。

这个系统的动能为

理论上杆的转动 α对小球移动的动能是有影响的，但现已忽略，所以式(1)中并未出现xα项，即忽略了这两个坐标之间的动态联系。

该系统的势能为

式中，g为重力加速度。

根据Lagrange方程式从式(1)和式(2)可得此球-杆系统的运动方程［20］为

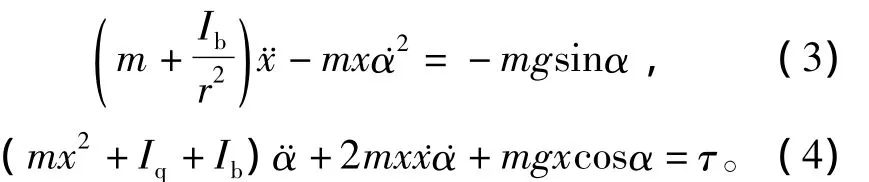
现在用频域反步法来进行设计。对球-杆系统的平衡点x=0来说，可以忽略式(3)和式(4)中的离心力项和哥氏加速度项，并令α→0°，得平衡点x=0处的线性化方程为

代入具体参数后为

式中:x的量纲为m;α的量纲为rad;u的量纲为V。

频域反步法设计是先从低维的子系统开始的，对该子系统设计一个虚拟的控制输入。结合式(7)来说，这第一步的子系统为

式中，uα为代替α的虚拟控制。式(9)的系统比较简单，可采用一般的PD控制，即

取此系统的一对极点为-2、-2，可得比例项和微分项的系数分别为

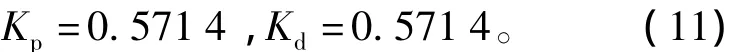
但是实际上α才是式(7)系统的真正输入，设α与uα的误差为Z1=α-uα，所以反步法的第二步是设计式(8)中的控制律u(即输入力矩)来减少这个Z1，即使α收敛于这个虚拟的控制量uα。

图2为用上述思路进行反步法设计的框图，图中虚线右侧就是与式(7)和式(8)对应的球-杆系统。图中的Kα(s)为这第2步要设计的控制器。图中从u到误差信号-Z1之间整个系统的传递函数关系是第2步设计中的对象特性，设用G(s)来表示。由于现在的传递函数关系比较复杂，故第2步宜采用H∞设计，而这个G(s)就是H∞设计中的广义对象。这一步设计中系统的高频段和低频段要求是比较容易确定的，而对象的正反馈回路中又存在虚轴上的特征值，故这一步宜采用H∞回路成形设计［21］。H∞回路成形设计中控制器由两部分构成，即

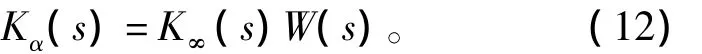
式中:K∞(s)为要通过回路成形来设计的H∞控制器;W(s)为权函数，是用来反映所要求的系统的高低频特性。设W(s)中的增益为K1，则由图2可知，这个α回路的低频特性可近似看成是3.495K1/s2，这个低频段特性以-40 dB/dec的斜率在ωc1=处穿越0 dB线，这个ωc1反映了角度α回路的带宽大小。故设计中取K1=50，使α回路的带宽约为20 rad/s。另外，Kα(s)的高频段应该有较快的衰减以削弱高频噪声的影响，保证系统的鲁棒性以及降低对u值的瞬间要求，故最终取W(s)为

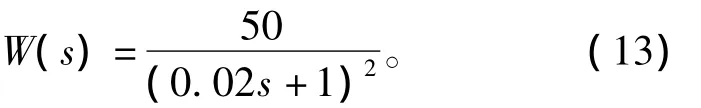
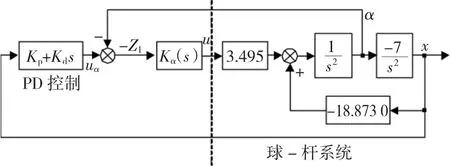
图2 控制系统的构成Fig．2 Formation of the control system

H∞成形设计时这个W(s)与对象G(s)构成成形对象Gs(s)=G(s)W(s)。将Gs(s)组成如图3所示的标准H∞成形设计框图，其中w= [w2]T和z= [z1z2]T分别为回路成形法中的输入和输出。利用MATLAB的hinfsyn函数，求解从w到z系统Tzw的H∞优化问题，得系统的H∞范数为

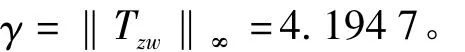
满足回路成形法γ＜5的鲁棒性设计要求［21］。所得的H∞控制器为

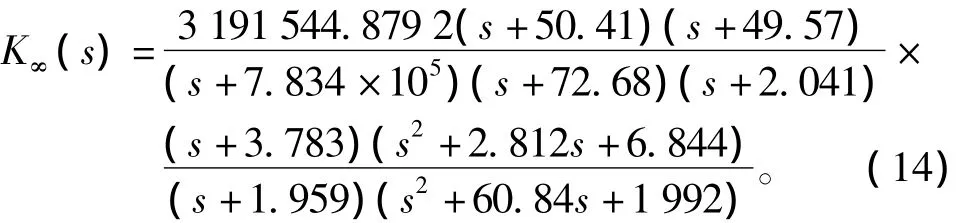
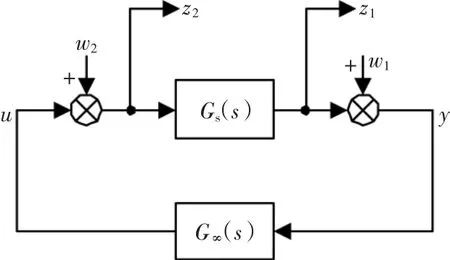
图3 回路成形的设计框图Fig．3 Block diagram for the loop shaping design

根据式(12)得最终的球-杆系统的α回路的控制器为

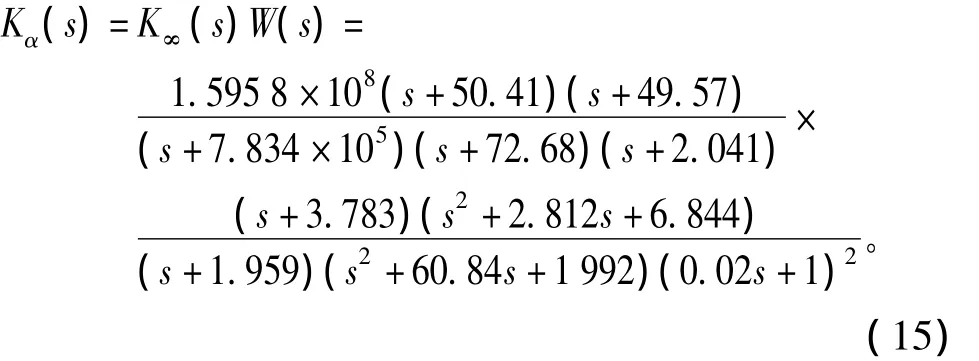
图4为控制器的Bode图，由图4可知，Kα(s)的幅频特性在高频段有较大的衰减，满足设计要求。图5以及图6中的曲线a为所设计系统在α回路和x回路分别断开时的Nyquist图线，即在Kα前断开和在PD前断开得到的图线。由图5和图6可见，无论从哪个回路看，系统都具有相当大的稳定裕度，因而也具有足够的鲁棒性。图5中曲线的开裂点对应于图2中正反馈回路虚轴上谐振模态的∞半径。

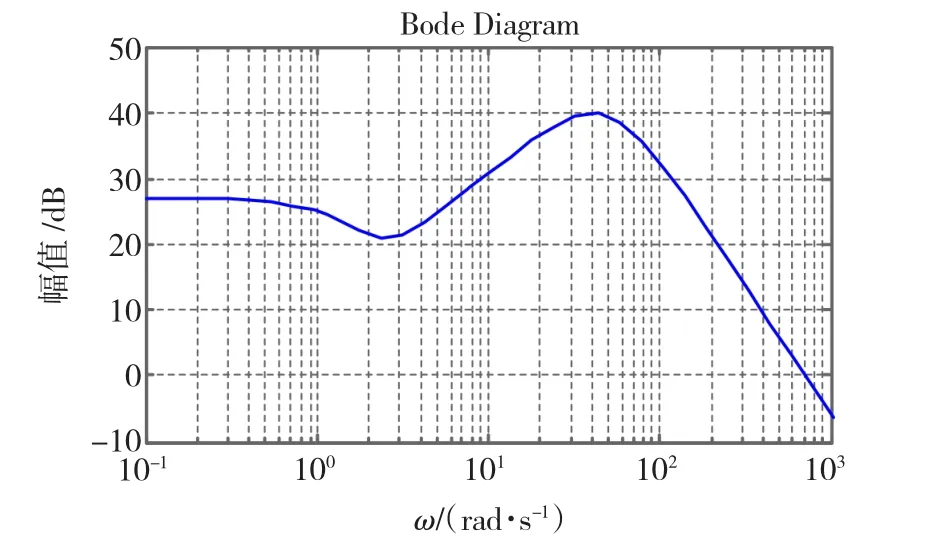
图4 控制器Kα(s)的Bode图Fig．4 Bode plot of the controller Kα(s)

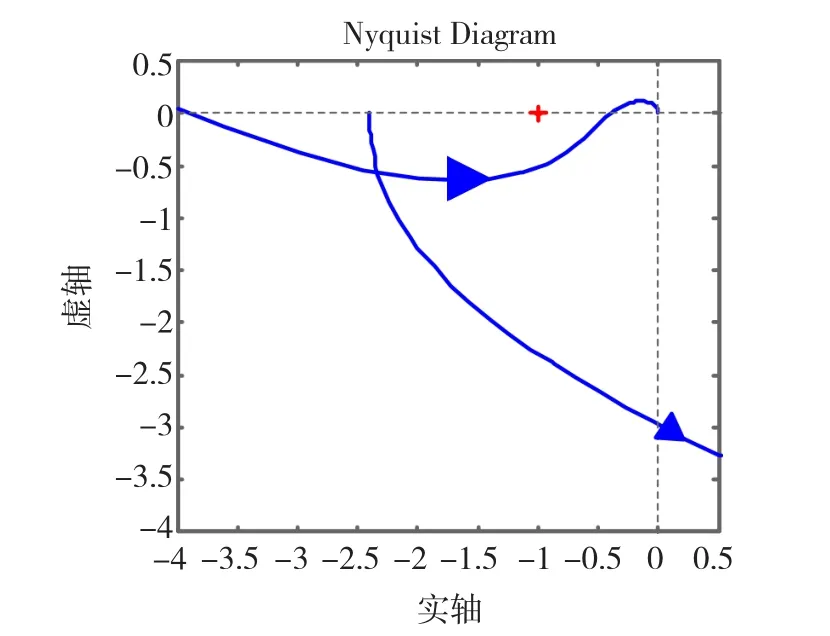
图5 角度α回路的Nyquist图Fig．5 Nyquist plot of the angle loop

图6中也绘出了反步法第一步对x采用虚拟控制uα时的Nyquist图线b。虚拟控制下的对象是双积分环节，而现在的对象则是开环不稳定的，虽然是完全不同的对象特性，但是在反步法设计后，在-1点附近的区域，仍然逼近虚拟控制时所指定的特性，即具有非常相似的稳定裕度。这也就是本文的反步法设计的特点和优越性，即系统的主回路(外回路)特性可以采用简单的PD设计来给定，再用反步法设计来给于保证。

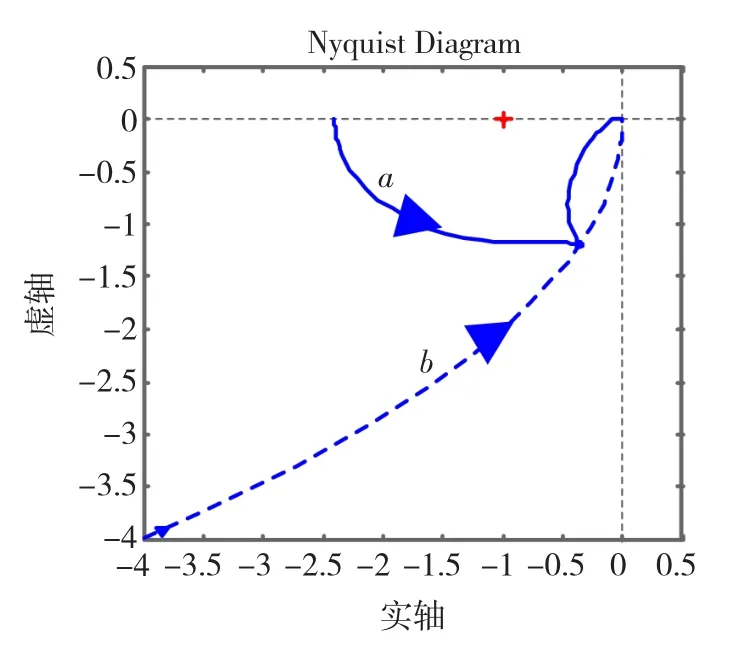
图6 球位置x回路的Nyquist图Fig．6 Nyquist plot of the position loop

这里要说明的是，上面的设计只是工作点附近的线性化系统的设计。当偏差增大时，非线性系统的特性就显现出来了。图7为所设计的控制器在不同初始条件下的调节过程，仿真中用的对象模型为式(3)和式(4)的非线性方程组。由图7可知，当偏差增大时，x(t)的初始的反向超调和α(t)曲线上的反向峰值急剧增大，所要求的功放级的控制电压u(t)出现很高的尖峰。

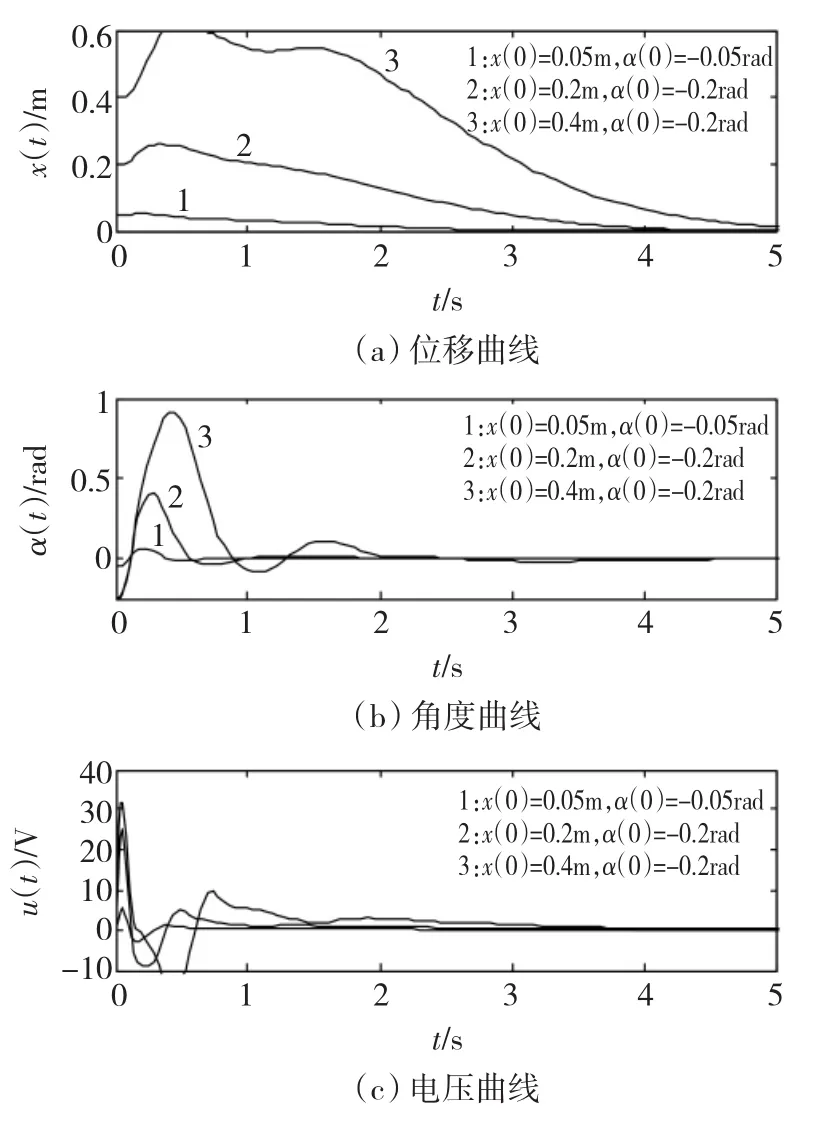
图7 不同初始条件下的调节过程Fig．7 Transient responses under various initial conditions

图7中的尖峰现象是非线性系统所特有的非线性现象，是由线性化时所忽略的未建模非线性引起的。具体来说，是由式(3)中的离心力xα2项所引起的，这一项随 α的平方而增长，很快会超过式(3)中对系统起镇定作用的sinα项，而形成一个很强的正反馈作用，又助长 α的增长，最终可导致不稳定。这里虽然是结合球-杆系统来说的，但尖峰(peaking)现象却是一种典型的非线性现象［11］。Kokotovic在文献［11］中将这个现象称为 BB综合症(ball beam-syndrome)。对于这种非线性尖峰现象，一般可以用饱和特性来抑制尖峰项的增长［11，22］。结合本例来说，Amira公司的球 -杆系统功放级的限幅值为±10 V。图8为利用此限幅特性来抑制尖峰现象的仿真结果，由图8可见，各变量均已进入正常范围，不再有尖峰出现。图8在仿真时还考虑了小球的行程限制。该球-杆系统的行程为±0.4 m，两端有止档。如图8所示的仿真情况对应于杆的初始角为-0.5 rad时，球停靠在一端的初始状态，代表了该球-杆系统正常工作时的最大工作范围(杆的转动也有止档限制，约±30°)。由上面的分析可知，虽然线性化设计忽略了系统的非线性特性，而且后者还可能引起严重的尖峰现象，但是只要适当运用反馈回路中的饱和特性，所设计的球-杆系统在实际的工作范围内都是能够稳定工作的。利用饱和特性来抑制非线性项的增长以保证稳定性，也是当前非线性系统设计的一个新的动向［23］。

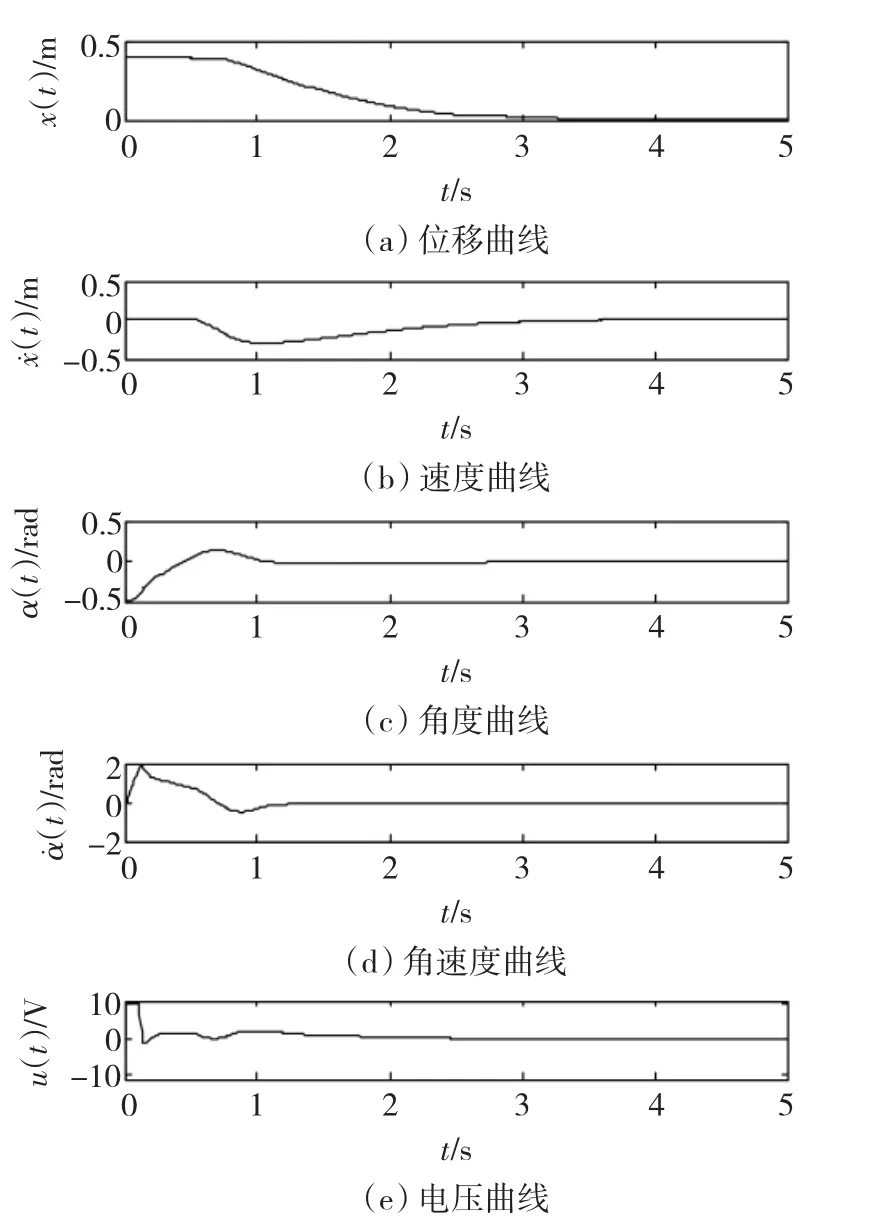
图8 功放级带饱和时的调节过程Fig．8 Transient responses under saturation

2 结语

本文结合欠驱动系统所提出的频域反步法，不同于状态空间反步法，是逐个回路递推进行的H∞设计。这种反步法的设计思路清楚，设计后的系统特性基本上可复现第一步虚拟控制回路的特性。而且由于是逐个回路的递推进行，一个回路设计一个控制器，所以系统实现是比较简单的。又因为采用了多重回路的结构，系统的鲁棒性也较好。虽然这是一种基于线性化的H∞设计，将系统的非线性归入未建模非线性，而且有可能出现尖峰，但是只要在反馈回路中适当引入饱和特性，就可避免尖峰现象，保证系统的稳定。除欠驱动系统外，频域反步法也可应用于其他各类系统的设计。

［1］KOLMANOVSKY I，MCCLAMROCH N H.Developments in nonholonomic control problems［J］.IEEE Control Systems Magazine，1995，15(6):20-36.

［2］REYHANOGLU M，VAN DER SCHAFT A，MCCLAMROCH N H，et al.Dynamics and control of a class of underactuated mechanical systems［J］.IEEE Transactions on Automatic Control，1999，44(9):1663-1671.

［3］刘盛平，吴立成，陆震.PPR型平面欠驱动机械臂的点位控制［J］.控制理论与应用，2007，24(3):435-439.

LIU Shengping，WU Licheng，LU Zhen.Point-to-point control of a planar prismatic-prismatic-revolute(PPR)under-actuated manipulator［J］.Control Theory and Applications，2007，24(3):435-439.

［4］JIANG Z P，NIJMEIJER H.Tracking control of mobile robots:a case study in backstepping［J］.Automatica，1997，33(7):1393-1399.

［5］刘盛平，陆震，吴立成.垂直起降飞机的全局轨迹跟踪控制［J］.控制与决策，2007，22(8):899-902.

LIU Shengping，LU Zhen，WU Licheng.Global trajectory tracking control of VTOL aircraft［J］.Control and Decision，2007，22(8):899～902.

［6］岳李勇，谢巍.含有驱动器模型的移动机器人自适应跟踪控制［J］.控制理论与应用，2008，25(6):1001-1006.

YUE Liyong，XIE Wei.Adaptive tracking control of non-holonomic wheeled mobile robot including actuator dynamics［J］.Control Theory and Applications，2008，25(6):1001-1006.

［7］董国华，祝晓才，刘振，等.不确定曲面上轮式移动机器人鲁棒轨迹跟踪［J］.南京理工大学学报:自然科学版，2008，32(1):18-27.

DONG Guohua，ZHU Xiaocai，LIU Zhen，et al.Robust trajectory tracking of wheeled mobile robots moving on uncertain uneven surface［J］.Journal of Nanjing University of Science and Technology:Natural Science，2008，32(1):18-27.

［8］ORTEGA R，SPONG M W，GOMEZ-ESTERN F，et al.Stabilization of a class of underactuated mechanical systems via interconnection and damping assignment［J］.IEEE Transactions on Automatic Control，2002，47(8):1218-1233.

［9］NORDKVIST N，BULLO F.Control algorithms along relative equilibria of underactuated Lagrangian systems on Lie groups［J］.IEEE Transactions on Automatic Control，2008，53(11):2651-2658.

［10］HAUSER J，SASTRY S，KOKOTOVIC P.Nonlinear control via approximate input-output linearization:the ball and beam example［J］.IEEE Transactions on Automatic Control，1992，37(3):392-398.

［11］KOKOTOVIC P V.The joy of feedback:nonlinear and adaptive［J］.IEEE Control Systems Magazine，1992，12(3):7-17.

［12］KOKOTOVIC P V，ARCAK M.Constructive nonlinear control:a historical perspective［J］.Automatica，2001，37(5):637-662.

［13］周绍生，费树岷，冯纯伯.多输入非线性串级系统的H∞控制［J］.自动化学报，2001，27(2):214-218.

ZHOU Shaosheng，FEI Shumin，FENG Chunbo.H∞control of multi-input cascade nonlinear systems［J］.Acta Automatica Sinica，2001，27(2):214-218.

［14］HE Yuqing，HAN Jianda.Acceleration feedback enhanced H∞disturbance attenuation control［C］//The 33rd Annual Conference of the IEEE Industrial Electronics Society(IFCON)，November 5-8，2007，Taipei，China.2007:839-844.

［15］VAN DER SCHAFT A.非线性控制中的L2增益和无源化方法:2版［M］.北京:清华大学出版社，2002:125-134.

［16］KRISHNAMURTHY P，LU W，KHORRAMI F，et al.Robust force control of an SRM-based electromechanical brake and experimental results［J］.IEEE Transactions on Control Systems Technology，2009，17(6):1306-1317.

［17］SWAROOP D，HEDRICK J K，YIP P P，et al.Dynamic surface control for a class of nonlinear systems［J］.IEEE Transactions on Automatic Control，2000，45(10):1893-1899.

［18］SHIEH H J，HSU C H.An integrator-backstepping-based dynamic surface control method for a two-axis piezoelectric micropositioning stage［J］.IEEE Transactions on Control Systems Technology，2007，15(5):916-926.

［19］王广雄，何朕.应用H∞控制［M］.哈尔滨:哈尔滨工业大学出版社，2010:123-128.

［20］何朕，王毅，周长浩，等.球-杆系统的非线性问题［J］.自动化学报，2007，33(5):550-553.

HE Zhen，WANG Yi，ZHOU Changhao，et al.Nonlinear roblems of the ball-and-beam system［J］.Acta Automatica Sinica，2007，33(5):550-553.

［21］何朕，孟范伟，刘伟，等.H∞回路成形法的鲁棒性［J］.自动化学报，2010，36(6):890-893.

HE Zhen，MENG Fanwei，LIU Wei，et al.Robustness of H∞loop shaping design［J］.Acta Automatica Sinica，2010，36(6):890-893.

［22］KHALIL H K.非线性系统:3版［M］.北京:电子工业出版社，2005:454-461.

［23］SU Y，MÜller P C，ZHENG C.Global asymptotic saturated PID control for robot manipulators［J］.IEEE Transactions on Control Systems Technology，2010，18(6):1280-1288.