无刷直流电动机转子退磁故障的检测方法

赵向阳， 葛文韬

(北京航空航天大学自动化科学与电气工程学院，北京 100191)

0 引言

随着稀土永磁材料、电力电子、新型控制理论及电机理论的进步，无刷直流电机的技术发展十分迅速，由于无刷直流电动机采用高磁能积稀土永磁材料，具有结构简单、运行可靠、体积小、质量轻、损耗小、效率高、运行特性优良等优点，广泛用于数控机床、伺服系统、机器人以及航空航天、航海等领域。特别是在一些军工领域，电机的电磁负荷较高，去磁磁场大，电机内温度较高，且运行环境恶劣。一旦电机发生故障，将会对系统造成较大的影响，故有必要对电机的健康状态进行在线监测，以便早期发现故障，及时处理，并采取措施进一步提高电机的可靠性。

本文主要针对退磁故障进行研究。转子退磁故障主要是由于腐蚀、磁缺损、裂纹、过载或者绕组短路等原因产生的高温，造成永磁体的部分或整体磁性能下降。对于此类故障如果不加以监测，会产生较为严重的后果。如钕铁硼永磁体生产时可能会有一些细微的裂纹，在电机的高速运行过程中，这些裂纹就会分解，从而产生碎片，进入到电机的气隙中，进而使摩擦增加，定子绝缘损坏，最终导致电机的损坏。特别是当电机内的温度超过居里温度时，将造成不可逆退磁［1－3］，对电机造成永久性的影响。

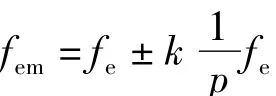
1 无刷直流电动机系统的模型

1.1 无刷直流电动机本体模型

假设磁路不饱和，并不计涡流和磁滞损耗，且三相绕组对称，则无刷直流电机的电压平衡方程［9］可以表示为

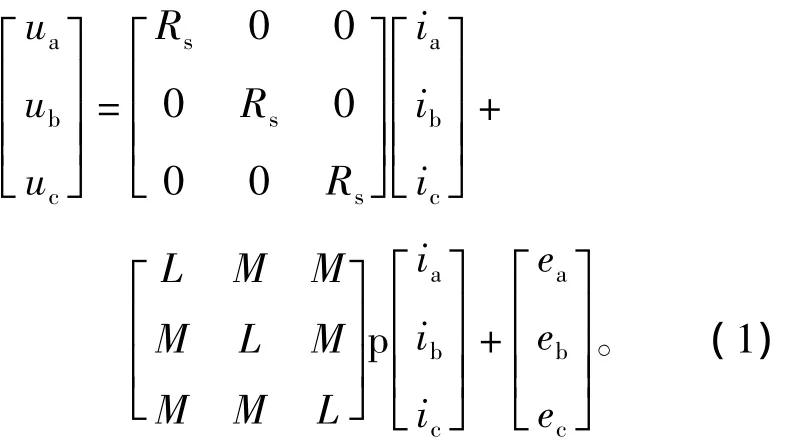
由于定子三相绕组采用Y型连接，因此有ia+ib+ic=0，从而得到

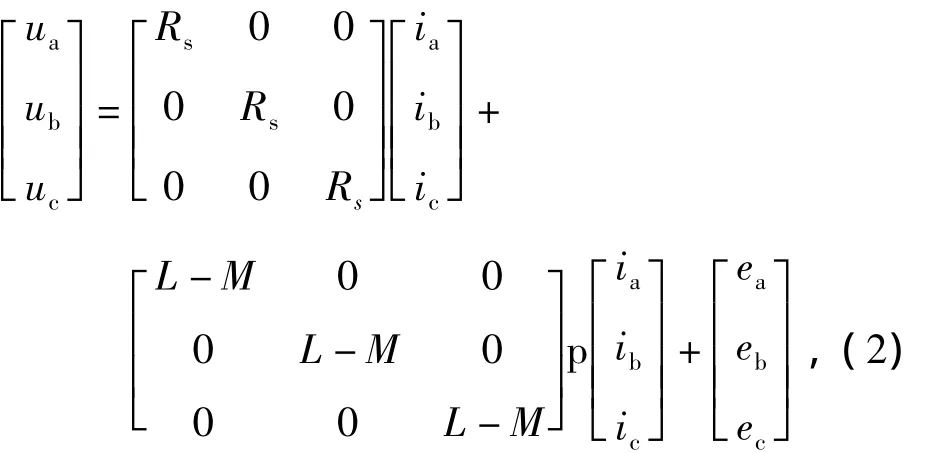
其中:Rs为定子每相绕组的电阻(Ω);L为定子每相绕组的自感(H);M为定子任意两相绕组间的互感(H);p为微分算子;ua，ub，uc表示三相定子电压(V);ia，ib，ic表示三相定子电流(A);ea，eb，ec表示三相反电动势(V)。

电动机的电磁转矩方程为

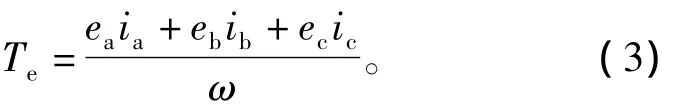
运动方程为

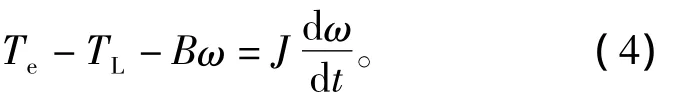
其中:Te表示电磁转矩;TL表示负载转矩;B表示阻尼系数;ω表示电机机械转速;J表示电机的转动惯量。

根据无刷直流电动机的数学模型，即可在Simplorer平台下搭建无刷直流电动机的仿真模型。如图1所示，左侧框图表示电机的电压平衡方程，右上角框图表示电机的转矩和运动方程，右下角的框图表示三相的反电势。

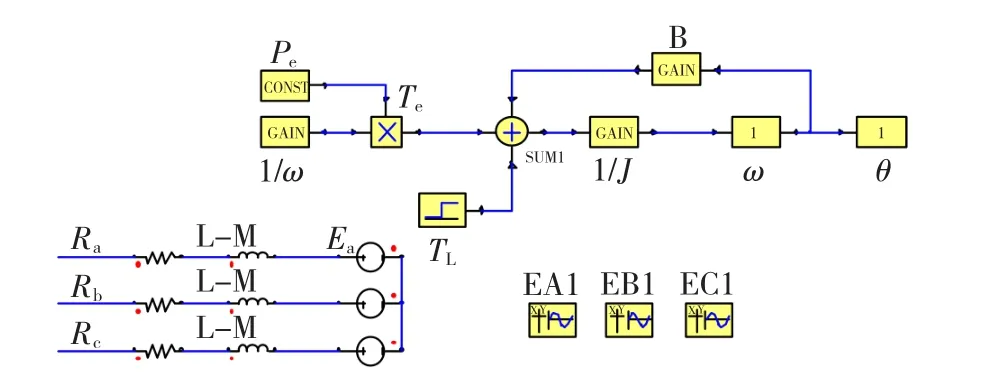
图1 无刷直流电动机的仿真模型Fig．1 Simulated model of BLDC

1.2 反电动势的求解

反电动势的求解一直是无刷直流电动机建模时较难解决的问题，反电动势波形不理想会造成转矩脉动增大，相电流波形不理想等问题，严重时甚至会导致换相失败，电机失控。因此，准确求解反电动势波形是无刷直流电动机仿真建模的关键问题之一。反电动势的波形与永磁体性质、形状，齿槽结构以及绕组方式有关［10］。目前求取反电动势较常用的方法有三种［11］:(1)有限元法。应用有限元法求得的反电动势脉动小、精度高。但方法复杂，专业性强。(2)傅里叶变换法。傅里叶变换法应用简单，但需要进行大量三角函数值的计算，对仿真速度影响较大。(3)分段线性化法。分段线性化法应用简单，计算量小，但只适用于反电动势波形比较规则的情况。

电机转子发生故障后，特别是局部磁缺损故障，其反电动势不再是理想的梯形波，需要进行特殊处理。因此，如何准确计算电机故障状态下的反电动势，是建立故障模型的关键。

图2所示为通过瞬态电磁场有限元计算求得的电机A相绕组反电动势波形。可以看出，在反电动势波的120°范围内，即使在健康状态下，反电动势波形也不是理想的平顶波。这是因为本文电机采用整数槽集中绕组，故定子齿槽对磁场分布的影响较大［12］。在故障状态下，由于磁缺损的影响，使电机的反电动势产生大幅度下凹，不再是理想的梯形波。本文仿真的电机为3对极，故转子旋转一周，反电动势变化3个周期。

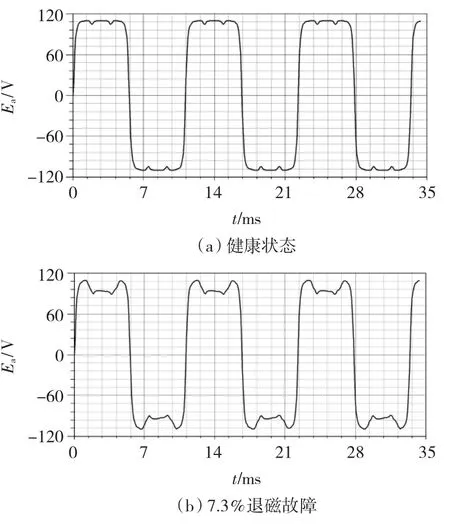
图2 无刷直流电动机的反电动势波形Fig．2 Back EMF waveform of BLDC

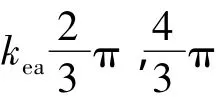
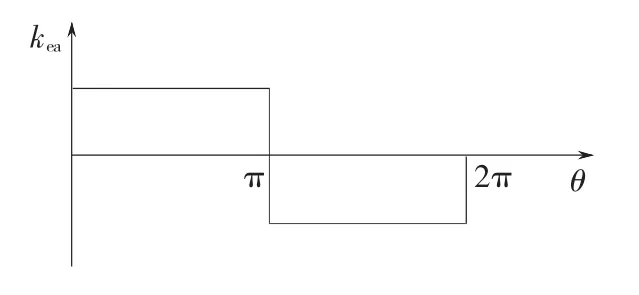
图3 反电动势常数与转子位置的关系Fig．3 Back EMF constant versus rotor position

具体做法如下:

1)首先在Ansoft/Maxwell 2D软件平台下，在空载状态下令电机恒速运行一周，即可求得空载条件下的电机三相反电动势。

2)将所求反电动势除以角速度ω，即可算出电机反电动势常数KE与转子转角位置的关系。

3)将其储存为一个表格，仿真时通过查询表格即可得到反电动势常数的数值。如图1中右下角框图所示。

这种方法应用简单，精度高，特别适合反电动势波形不规则的情况。

2 基于定子电流特征频率的转子退磁故障仿真

2.1 理论基础

无刷直流电动机转子产生退磁故障，使永磁体的磁性能受到影响，进而使气隙磁通发生畸变，最终使故障体现在定子电流中。因此，通过监测电机的定子电流，即可以对退磁故障进行探测。

如图2(b)所示为电机局部磁缺损故障的反电动势波形图。电机的转子旋转一周，反电动势变化3个周期。因此，退磁故障的特征频率为电机旋转频率的3倍。如果电机有p对极，则定子电流的频率为旋转频率的p倍。即局部磁缺损故障的特征频率与定子电流的频率相同。

若电机发生整体退磁故障，则反电动势波形与健康状态下的反电动势波形相同，只是在相同的转速下，幅值发生变化，故也不会产生新的特征频率。故无法区分整体退磁故障与局部退磁故障。

2.2 故障设置

本文针对转子的退磁故障进行仿真研究。主要包括局部磁缺损故障和整体退磁故障。具体设置方法如下:

1)磁缺损故障:在Ansoft/Maxwell软件平台上，将电机永磁体的磁性材料切割掉一部分，即可模拟局部磁缺损故障。

2)整体退磁故障:在Ansoft/Maxwell软件平台上，通过修改转子永磁体的B－H曲线，即可模拟整体退磁故障。

2.3 仿真研究

本文针对一台6极，2 kW，表贴式转子的无刷直流电动机进行仿真研究。采用转速、电流双闭环的控制方式。转速给定为1500 r/min，负载转矩为3 N·m。

无刷直流电动机定子电流的频率为电动机正常运行时逆变器开关状态的频率，可以表示为

其中:s表示一个电气周转内开关状态的变化次数;p表示电机的极对数;n表示电机的转速。

图4所示为无刷直流电动机在健康状态下和20%退磁故障下，电机在稳态运行时A相绕组电流的频谱图。

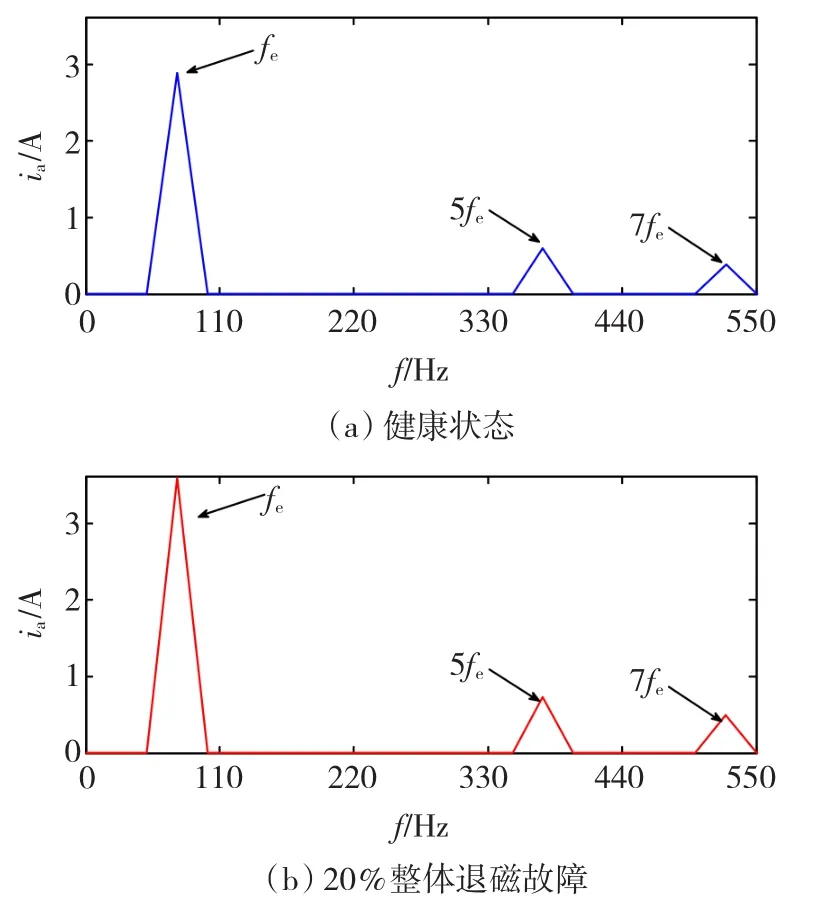
图4 无刷直流电动机定子A相电流频谱图Fig．4 Spectrum of stator current

与健康状态下的电机相比，电机发生退磁故障后，定子电流随之增加。由于5次和7次谐波与转子作用产生的平均转矩是零，因此，可以将基波频率fe作为转子退磁故障的特征频率。通过监测基波频率fe的幅值即可以对电机的退磁故障进行探测。

在实际运行中，电机可能工作在某一转速范围内，为了能更清晰的判别故障，表1为在1 000～1 500 r/min范围内，负载转矩为3 N·m，以健康状态下的电机定子电流fe的幅值为基准，归一化后的定子电流频谱值。归一化的方法如下:

1)在某一恒定转速下，将健康状态下的基波频率fe的幅值分别作为基准值。

2)将故障状态下的fe的幅值分别与其健康状态下的幅值作比值。

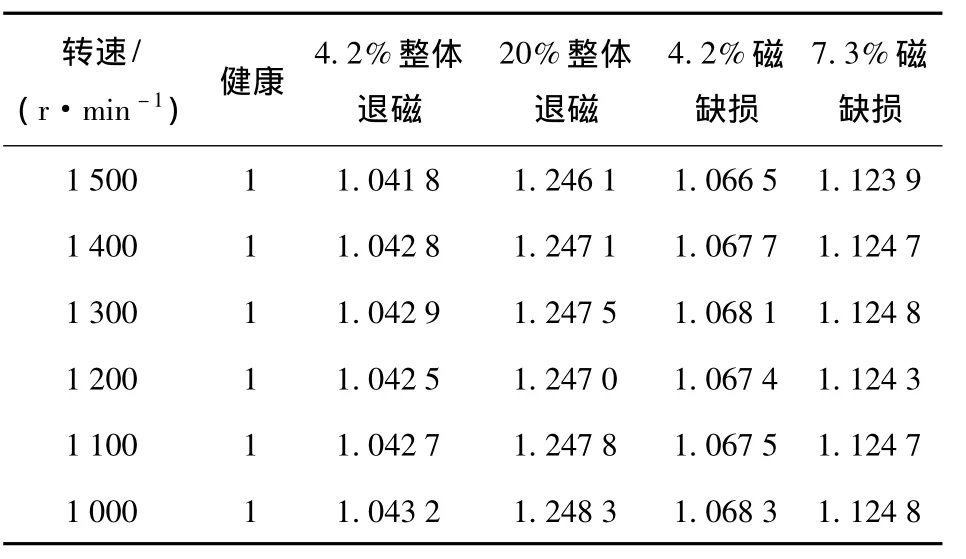
表1 基于定子电流法的退磁故障仿真结果Table 1 Simulation results based on MCSA

通过对比，可以看出:

1)故障程度加大，定子电流基波频率的幅值随之增加，采用定子电流法能有效地监测无刷直流电动机转子的退磁故障及故障程度。

2)仿真表明，与由于温度等原因造成的退磁故障相比，同等程度的磁性材料的缺损对电机性能会造成更大的影响。这是因为磁性材料缺损，不仅造成永磁体磁性能下降，另一方面也会使气隙长度增加。如在1 500 r/min的情况下，4.2%整体退磁故障和4.2%磁缺损故障对应的定子电流分别为1.041 8和1.066 5。20%整体退磁故障和20%磁缺损故障对应的定子电流分别为1.246 1和1.428 5。

3 基于转矩常数估计法的故障探测

3.1 探测原理

随着退磁程度的加大，定子电流也随之增加。这是因为转子发生退磁故障后，造成永磁体的磁性能下降，相应的转矩常数也随之减小。因此，为了产生恒定的转矩，将会使得定子电流进一步增加。对此，通过监测转矩常数的变化，同样可以对转子的退磁故障进行探测。

然而，在实际测量时，由于转矩常数较难直接测得，因此可以通过转矩常数估计值的变化探测退磁故障［10］。

假定在0～60°电角度之间，此时A相和B相导通，电流从A相流入，B相流出，C相关断，则可将式(1)简化为

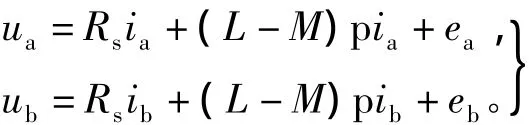
由于ia=idc=－ib，所以将上式中的A相与B相电压相减后可得

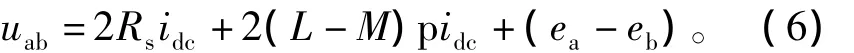
在稳态情况下，逆变器的电流在平均值附近线性的增加或者减少，因此通过取平均值可以近似的认为pidc=0。上式中的(ea－eb)是A相绕组反电动势和B相绕组反电动势的和，将其记为，并取每60°导通期间的电流平均值Idc和电压平均值V，则式(6)简化为:V≈2RsIdc+，即

将式(7)除以电机的角速度ω，即可得到用于探测无刷直流电动机转子退磁故障的转矩常数估计值［8］为

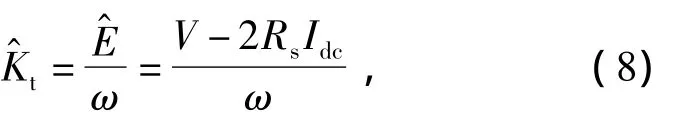
本文在推导式(8)的过程中，认为电机的电感在充放电过程中，电流上升时的斜率等于电流下降时的斜率，因而近似的认为pidc=0。但实际情况并非如此，特别是当电机的转速较低时，电流上升时的斜率远大于下降时的斜率，因此，转矩常数的估计值与转速有关。

3.2 仿真研究

表2给出了在1 000～1 500 r/min范围内，以健康状态下的电机转矩常数估计值为基准，归一化后的转矩常数的估计值。归一化的方法与3.3节中电流归一化的方法相同。

表2表明:

1)转子退磁程度增加，转矩常数随之减小，采用转矩常数估计法可以对转子的退磁故障进行探测。

2)与由于温度等原因造成的退磁故障相比，同等程度的磁缺损故障对应的转矩常数的估计估计值更小。如在1 500 r/min的情况下，4.2%整体退磁故障和4.2%磁缺损故障对应的转矩常数估计值分别为0.960 0和0.939 3，20%整体退磁故障和20%磁缺损故障对应的转矩常数分别为0.815 9和0.721 1。原因如表1中第2点结论中所述。

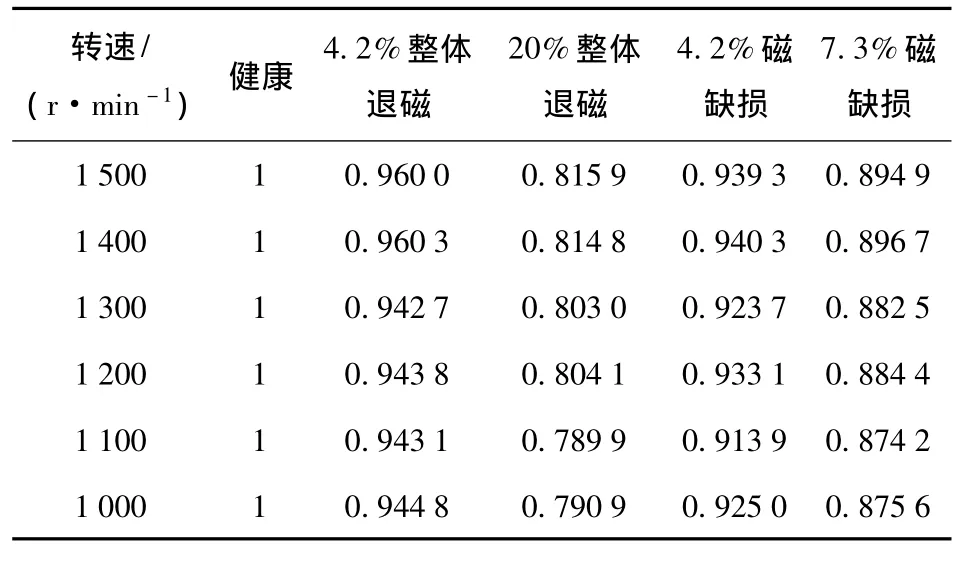
表2 基于转矩常数估计的退磁故障仿真结果Table 2 Simulation results based on the estimation of torque constant

4 结论

1)本文针对无刷直流电动机转子磁故障进行仿真研究，主要包括局部磁缺损故障和整体退磁故障。基于Ansoft/Maxwell软件平台设置退磁故障，基于Ansoft/Simplorer软件平台搭建了无刷直流电动机系统的仿真模型。结果表明，在稳态运行条件下，电机发生退磁故障，相应的特征频率幅值和转矩常数估计值有明显变化。退磁程度加大，特征频率的幅值随之增加，转矩常数估计值随之减小。采用定子电流分析法和转矩常数估计法可以对转子退磁故障进行探测。

2)在转速波动较小时，采用定子电流法的效果更好。当转速波动较大时，由于FFT是基于稳态信号处理的方法，故定子电流法失效。可以采用转矩常数估计法。

3)若电机绕组采用不对称结构，发生局部磁缺损故障时，会在定子电流中产生与偏心故障相同的特征频率，此时定子电流法失效，可通过转矩常数估计法对转子的退磁故障进行探测。

4)由于本文仿真的电机采用的是集中整距绕组结构，因此并不能有效的区分转子的局部磁缺损故障与整体退磁故障。

［1］FAROOQ J A，DJERDIR A，MIRAOUI A．Analytical modeling approach to detect magnet defects in permanent-magnet brushless motors［J］．IEEE Transactions on Machines，2008，44(12):4599－4604．

［2］ESPINOSA A G，ROSERO J A，CUSIDO J，et al．Fault detection by means of Hilbert-Huang transform of the stator current in a PMSM with demagnetization［J］．IEEE Transactions on Energy Conversion，2010，25(2):312 －318．

［3］ROSERO J A，CUSIDO J，GARCIAL A．et al．Study on the permanent magnet demagnetization fault in permanent magnet synchronous machines［C］//32nd Annual Conference on IEEE Industrial Electronics，November 6 －10，2006，Paris，France．2006:879－884．

［4］LE ROUX W，HARLEY R G，HABETLER T G．Detecting rotor faults in low power permanent magnet synchronous machines［J］．IEEE Transactions on Power Electronics，2007，22(1):322－328．

［5］KIM Kichan，KIM Kwangsoo，KIM Heejun，et al．Demagnetization analysis of permanent magnets according to rotor types of interior permanent magnet synchronous motor［J］．IEEE Transactions on Machines，2009，45(6):2799－2802．

［6］CASADEI D，FILIPPETTI F，ROSSI C，et al．Magnets faults characterization for permanent magnet synchronous motors［C］//2009 IEEE International Symposium on Diagnostics for Electric Machines，Power Electronics and Drives，August 31 － September 3，2009，Cargese，France．2009:1 －6．

［7］RAJAGOPALAN S，LE ROUX W，HABETLER T G，et al．Dynamic eccentricity and demagnetized rotor magnet detection in trapezoidal flux(brushless DC)motors operating under different load conditions［J］．IEEE Transactions on Power Eelectronics，2007，22(5):2061 －2069．

［8］RAJAGOPALAN S，LE ROUX W，HABETLER T G，et al．Diagnosis of potential rotor faults in brushless DC machines［C］//Second International Conference on on Power Eelectronics，Machines and Drives，March 31－April 2，2004，Edinburgh，UK．2004，2:668－673．

［9］纪志成，薛花，沈艳霞．无刷直流电机调速系统模糊神经网络控制新方法［J］．电机与控制学报，2004，8(1):5 －9．

JI Zhicheng，XUE Hua，SHEN Yanxia．A novel fuzzy neural network control strategy of BLDCM speed servo system［J］．Electric Machines and Control，2004，8(1):5 －9．

［10］方卫中，贺益康．无刷直流电机反电势的人工神经元网络预测［J］．微电机，1998，31(2):7 －11．

FANG Weizhong，HE Yikang．Back electromotive force prediction using artificial neural network for brushless DC motor［J］．Micromotors Servo Technique，1998，31(2):7 －11．

［11］纪志成，沈艳霞，姜建国．一种新型的无刷直流电机调速系统的模糊PI智能控制［J］．电机与控制学报，2003，7(3):248－254．

JI Zhicheng，SHEN Yanxia，JIANG Jianguo．A novel fuzzy PI intelligent control method of BLDCM speed servo system［J］．E-lectric Machines and Control，2003，7(3):248 －254．

［12］孙宁，陈丽香，唐任远．无刷直流电动机的参数选择［J］．电气技术，2009(4):21－23．

SUN Ning，CHEN Lixiang，TANG Renyuan．Parameter selection in brushless DC motor［J］．Electrical Engineering，2009(4):21－23．