同步辐射用高频腔的性能研究实验

周 航，徐 杨，张新夷

（复旦大学物理学系，上海200433）

同步辐射用高频腔的性能研究实验

周 航，徐 杨，张新夷

（复旦大学物理学系，上海200433）

基于合肥光源提供的铜制有源高频腔和上海光源提供的铌制超导无源高频腔，设计了可以测量高频腔性能参量的实验装置.以探针将微波信号馈入高频腔体中，通过网络分析仪接收到的信号分析微波在腔体中的谐振情况，从而测量腔体的特性.利用该实验装置测量了2个高频腔的谐振频率、品质因数和腔体中心轴线上的电场分布.

高频腔；谐振频率；品质因数；电场分布

1 引 言

同步辐射（Synchrotron radiation）是指相对论性带电粒子在磁场中受洛伦兹力作用，沿弯转轨道行进时所发出的电磁辐射.同步辐射因具有高亮度、高准直、连续而宽广的频谱、偏振性及脉冲时间结构等优良特性而在基础科学、应用科学和工艺生产等领域有着广泛的应用［1－2］.

由于同步辐射在现代科学中的重要地位，有必要让高年级本科生对同步辐射相关技术有所了解；其次，通过本实验可以让学生应用电动力学中已学过的谐振腔的相关知识解决实际问题，如根据腔体尺寸计算腔体的谐振频率等；另外，在实验技术方面，也可使学生对网络分析仪的使用和微波技术等有所了解［3－4］.因此同步辐射实验是综合性、设计性和研究性都很强的近代物理实验.

2 实验原理

2.1 高频腔模式

实验所用的高频腔有2个，分别为合肥光源提供的铜制有源高频腔和上海光源提供的铌制超导无源高频腔.这2个高频腔均只用到TM010模式，在该模式下中心轴上磁场强度为零，电场沿轴方向（取为x轴，并且取中心轴线中点为零点）.若存在多个谐振模式，高频腔将会给储存环附加不稳定性，因此高频腔必须设计为单一模式起主要作用，而抑制其他模式.上海光源的无源超导铌腔（以下简称无源腔）由于其材料及结构的特殊性，抑制了其他高次模式，其中间凸起部分为高频腔区域，两端属于束流管道，为腔外电磁场截止区（见图1）.合肥光源的铜制有源腔（以下简称有源腔）为扁圆柱形高频腔，两端也有一段束流管道，最外层由金属包裹，外形如图2（a）所示.当高频腔置于储存环中时，束流管道（电子束轨道）应处于水平位置.由于在1个波导腔内，低频率的波容易被截止，这使得只有最低频率的基础模式在中间腔内谐振，高次模都从束流管道上传输出去耦合消除.

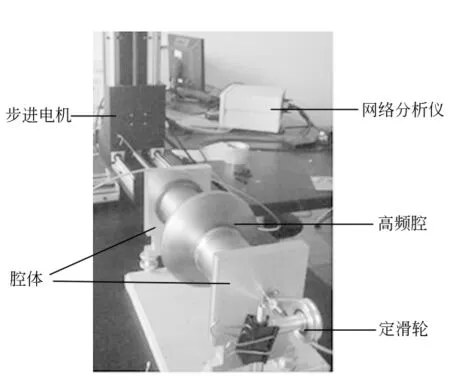
图1 无源腔实验装置

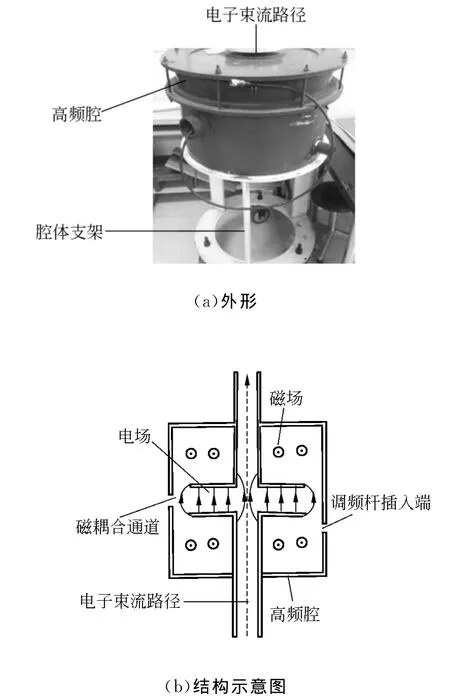
图2 有源腔实验装置

2.2 网络分析仪

网络分析仪是实验的主要设备，其上配置了信号发生器，可以对微波频段进行频率扫描测量.它有2个信号端口，都可以输出或输入信号.单端口测量状态下，将激励信号加在端口上，通过测量反射信号的幅度和相位，可以测量反射参量.双端口测量状态下，则可以测量阻抗等传输参量.网络分析仪设置模式及被测的物理量和相应的参量符号见表1.

表1 网络分析仪测量参量及模式

本实验中，可以将两端口分别连接探针置于高频腔的两端，通过测量1个频段下信号在两端口间的传输强度S21；或封闭高频腔的一端，只在其中一端连接探针，测量发射信号传输到封闭端再反射回来的强度S11，可以测量高频腔的谐振频率f；通过测量在加入不同微扰块后的谐振频率f，可以测量高频腔中的电场分布.

2.3 测量原理

2.3.1 谐振频率f

对于无源腔，其腔壁是封闭不开口的，在其两端口处分别连接一探针，固定于谐振腔的两端.将网络分析仪定标之后，测量1个频率范围内两端口间的传输信号强度S21与频率的关系曲线，高频腔的高次模式虽然都不在中间腔区域内谐振，但在束流管的两端可以产生共振，造成两探针间传输信号强度的吸收峰.实验中基频即为谐振频率，其他谐振峰为高次模的谐振.

对于有源腔这样的标准圆柱形谐振腔，一般可以采用磁耦合而非上述在腔两端加探针的电耦合的方式来测量谐振频率.磁耦合指在腔侧壁上接入一耦合天线金属环［参见图2（b）］，金属环的大小需根据腔内信号的强弱来调整.网络分析仪的信号传入金属环，金属环将其转化为在谐振腔内与腔中心轴垂直的磁信号，该磁信号就能激励出沿中心轴方向来回反射的电磁波信号，同样用网络分析仪测量信号强度与频率关系曲线，从而可测其谐振频率.有源腔侧壁有4个管道，其中1个为天线耦合通道，但天线部分已经破损不能使用.重新制作耦合天线需要拆开腔体，实验室不具备相应条件，因此未采用磁耦合方法，而是采用与无源腔相同的电耦合方法.

2.3.2 品质因数Q

品质因数Q表征储能器件（如电感线圈、电容等）或谐振电路所储能量同每周期损耗能量之比的质量指标，是元件的稳态参量.元件的Q值愈大，用该元件组成的电路或网络的选择性愈佳.电抗元件的Q值等于它的电抗同等效串联电阻的比值.谐振腔的品质因数有2种情况：一种是固有品质因数Q0，这是相对于孤立的腔体而言的；另一种是有载品质因数QL，顾名思义为腔体通过孔或缝、环或探针等耦合机构与外界（负载）发生能量耦合时的情况.为了测量Q0，可用如下Q0与QL的关系式得到：

其中Qc为耦合（或称外部）品质因数.为了说明腔体与外界负载之间的耦合程度，可以用耦合系数β来衡量，定义为β＝Q0／Qc，因此

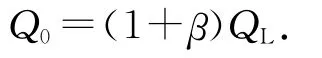
品质因数的测量采取将待测腔接在网络分析仪的测量端口，在其谐振点附近测出反射系数Γ（反射电压与入射电压之比）随频率f变化的曲线，有载品质因数QL＝f0／Δf，其中Δf＝f2－f1，即腔体吸收功率的半功率带宽.由文献［5］，半功率带宽为

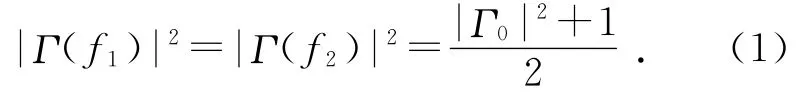
其中Γ0为谐振时的反射系数.由耦合系数方程

可得到β的具体数值.

由文献［6］，被测端口驻波比（波腹电压与波节电压之比，简写为SWR）的倒数即为其耦合系数.由于实验是双端口测量，两端口的耦合系数分别为β1和β2，因此原Q0与QL的关系式变为

由此可得到谐振腔的固有品质因数.

2.3.3 基模的电场分布测量

根据Slater微扰法理论，微扰体引起的频率偏移由当地的电场和磁场的强度决定，即：

其中K1～K4是常量.通过选择不同性质的微扰体，使其只对所关心的模式的某个分量起作用，这样频率偏移量就能反映场分量的幅值.测量频率偏移量，就能得到电场相对强度的分布E（z）∝

3 实验装置设计与搭建

3.1 探针形式与安装位置

探针的设计主要考虑：需要探测到足够大的信号强度，以增大信噪比；尽可能避免对高频腔的干扰，以免影响微扰方法的测量.在谐振模式下，与中心轴线垂直的截面上，电场在中心轴线上最强，故探针应尽可能置于靠近中心轴的位置.由于中心轴上有支撑微扰体的细线穿过，因此探针固定的实际位置需偏离中轴一定距离.实验时，将探针插入高频腔两端的束流管道内，以获得可行的信号强度；并且使两端探针相对，都平行于中轴.无源腔探针长度为65mm，直径为5mm，其固定的实际位置距离中轴约为12mm.有源腔两端束流管道长分别为25.5cm与21.5cm，因腔体为扁平的圆柱，在腔外衰减很快，因此两探针长度分别选择为25cm与21cm.

探针材料为紫铜.探针用于测量时，需要屏蔽探头以外的部分，以达到固定位置的测量效果.由里到外依次用绝缘胶布、铝箔、绝缘胶布3层材料包裹探针，达到屏蔽非探头部分的效果.

3.2 微扰装置

微扰体的材料选择常见的金属铜，作为良导体，其对电磁场的扰动显著.由于中心轴上电场沿轴方向，将微扰体外形设计为圆柱状，其长度大于直径，使得对电磁场的扰动集中于沿轴方向.频率扰动的大小正比于体积，但作为微扰条件，扰动不能太大，而为得到较好的测量精度，微扰量又需要一定的值.我们从直径确定的铜管上截不同长短的小铜柱进行对比实验，因此在微扰体材料直径已确定的前提下，考虑其长度与高频腔谐振区域长度大致的比例关系，有源腔选择微扰体铜柱的长度为14mm，直径为10mm；无源腔的微扰体铜柱长度为9mm，直径为4mm.

微扰体的支撑介质位于中心轴上，贯穿整个腔体，因此支撑材料本身对腔内电磁场的影响应尽量小.初步分析支撑材料应该不导电且体积与整个腔体体积相比可忽略.根据参考文献［3］的对比测量结果，细线产生的影响较小，故仍用细线支撑微扰体.用于无源腔测量的小铜块直径很小，实验时将细线穿过微扰小铜块并在小铜块两端各打一结以固定铜块，细线从腔两端穿出后一端接在步进电机上，另一端绕过定滑轮连上配重以拉直细线.用于有源腔的微扰铜块直径较大，因此在铜块两端各放置一小片塑胶片使铜块固定在细线上，连着小铜块的细线竖直穿过腔体，一端绕过放置在腔体上面的定滑轮后成水平方向连接到步进电机上，另一端直接连接配重.

4 实验结果与讨论

4.1 谐振频率

如表2设置网络分析仪参量，在对数增益模式下测量S21，以第一个峰值处频率为谐振频率.先粗测以确定细测范围，细测读出谐振频率f，结果见图3.对有源腔和无源腔，频率f分别读到0.01MHz和0.000 1GHz，并在测量范围内等间距读数，取数据点为800，其不确定度uf分别取为扫频范围10.0MHz和0.100GHz与测试数据点数800的比值.测量得到有源腔的谐振频率为（204.94±0.01）MHz；无源腔的谐振频率为（1.584 3±0.000 1）GHz.

表2 测量谐振频率时网络分析仪的参量设置

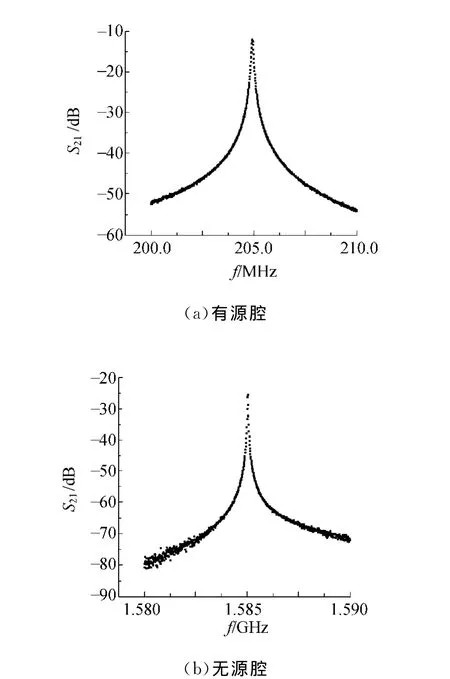
图3 谐振频率测量图

4.2 品质因数

首先测量有载品质因数QL.在对数增益模式下测量S11.对于QL的图像，从最低点横轴可以得到谐振频率f0，该频率应与之前测出的谐振频率一致，而最低点纵轴Γ0为谐振时的反射系数，由式（1）可得Γ（f1）和Γ（f2）及其对应的频率f1和f2，算出半功率带宽Δf，并可得到QL.

再测量耦合系数β1和β2.在端口驻波比模式下，测参量在测β1时选S11，测β2时选S22，波谷处的纵坐标值取倒数即得该端口耦合系数β.

网络分析仪参量设置见表3，这里接收机分析带宽设为1kHz是为了使仪器扫描变慢变稳定，便于读出更精确的值.

表3 测量品质因数时网络分析仪的参量设置

4.2.1 有源腔测量结果

图4是对数增益模式下S11随频率变化曲线，读取数据得到波谷处f0＝204.943MHz.结合式（1）并在图中找到对应f1和f2，得到半功率带宽Δf＝0.075MHz，从而得到有载品质因数QL＝f0／Δf＝2 732.573，不确定度uQL＝515.

图4 有源腔在对数增益模式下S11随频率变化曲线

在驻波比模式下测S11和S22，曲线见图5.由图5（a）可得，波谷处驻波比为4.902 7，因此β1＝0.204 0；由图5（b）得，波谷处驻波比为3.639 5，

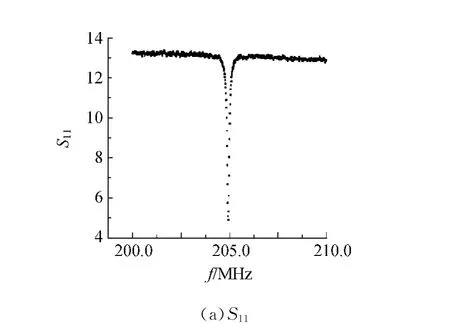
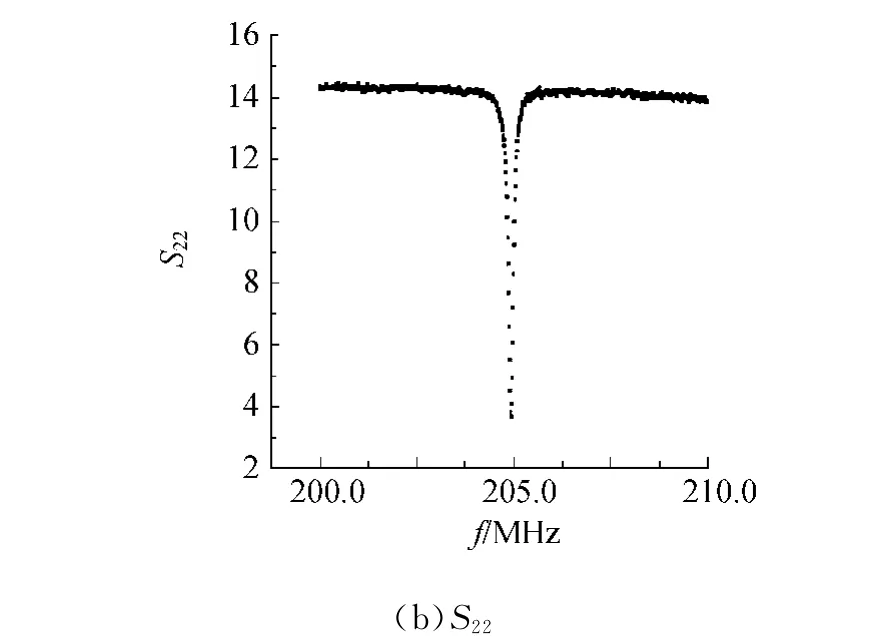
图5 有源腔驻波比模式下S11和S22随频率变化曲线

因此β2＝0.274 8.有源腔的固有品质因数为：

4.2.2 无源腔测量结果

在对数增益模式下测S11，数据导出到Origin作图如图6所示.

图6 无源腔在对数增益模式下S11随频率变化曲线

读取数据得到波谷处f0＝1.584GHz.结合式（1）并在图中找到对应f1和f2，得到半功率带宽Δf＝0.000 29GHz，从而得到有载品质因数：QL＝f0／Δf＝5 462.069，不确定度uQL＝232.

在驻波比模式下测S11和S22，曲线见图7.由图7（a）可得，波谷处驻波比为2.998 2，因此β1＝0.333 5.由图7（b）可得，波谷处驻波比为4.860 5，

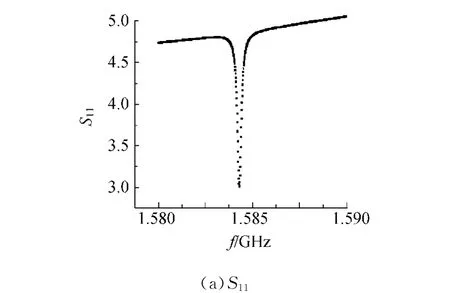
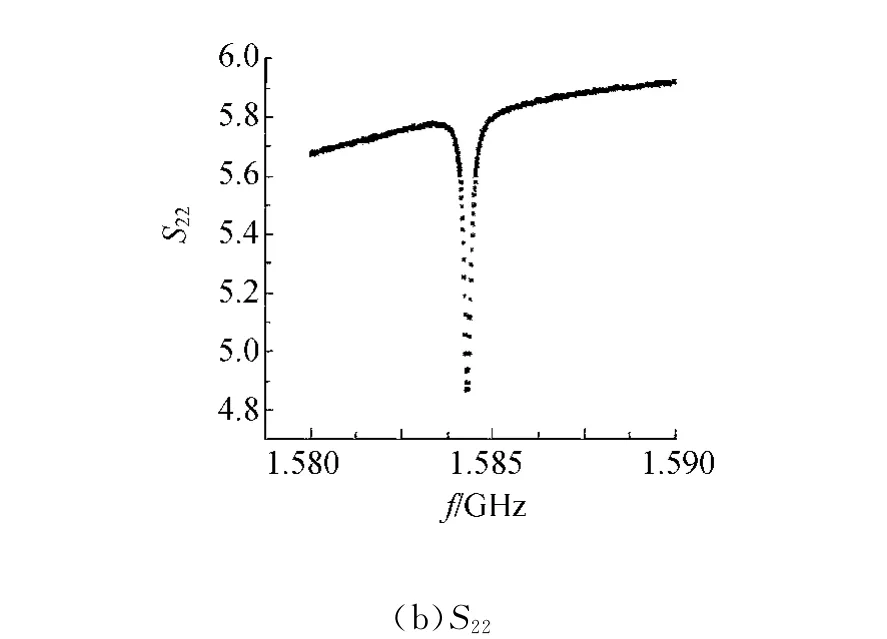
图7 无源腔驻波比模式下S11和S22随频率变化曲线

因此β2＝0.205 7.无源腔的固有品质因数为：

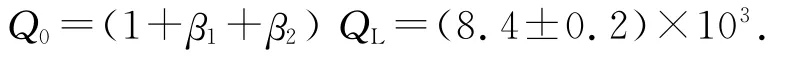
4.3 电场分布

将固定好微扰块的细线穿过高频腔，一端绕过定滑轮接在步进电机上，另一端连接配重.步进电机带动细线及微扰块在高频腔中轴线上移动.网络分析仪参量设置同表2.每隔5mm记录1次当前频率值，步进总长度为300mm.

谐振频率与微扰体位置变化曲线见图8.

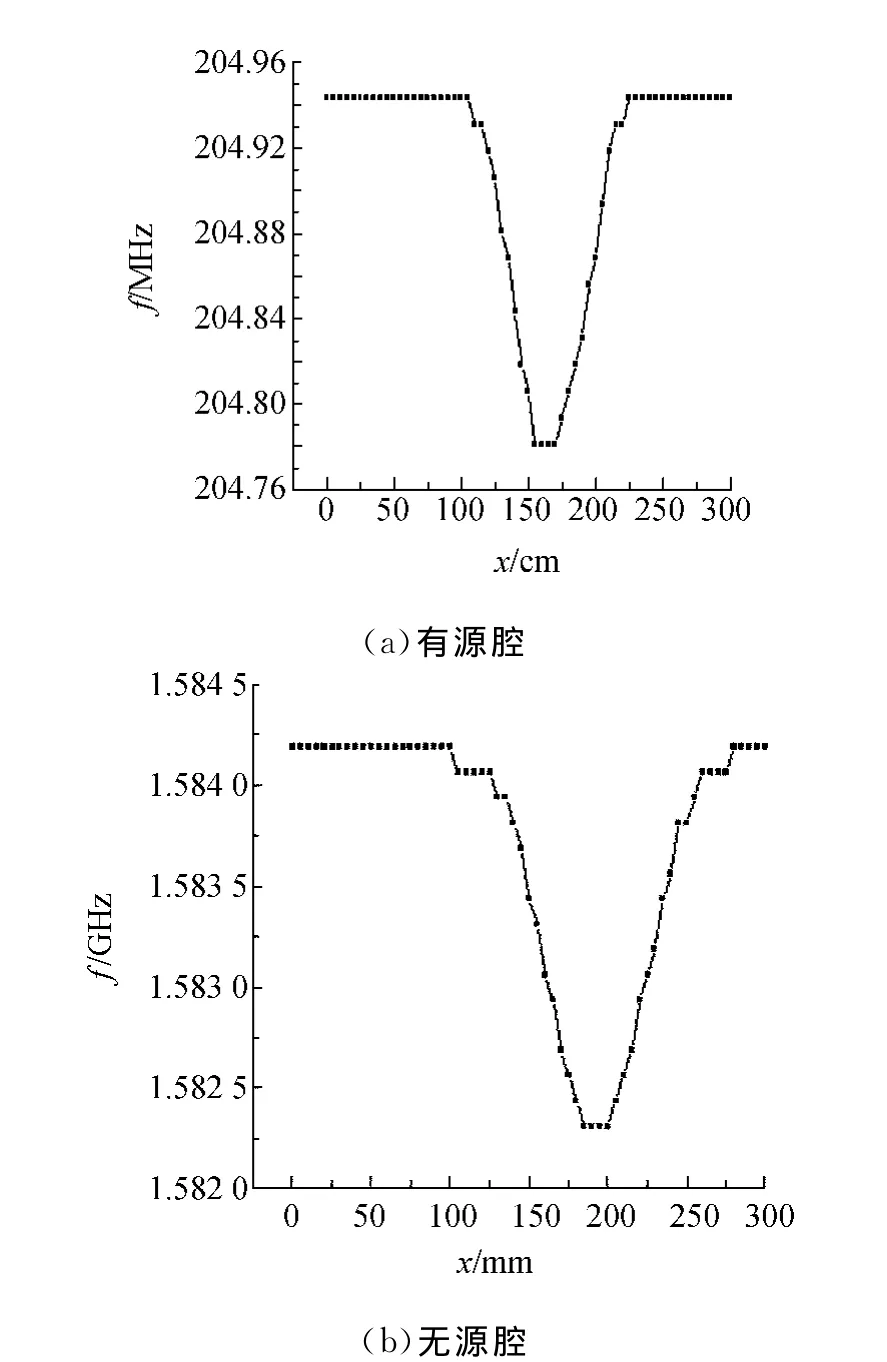
图8 谐振频率随微扰体位置变化曲线

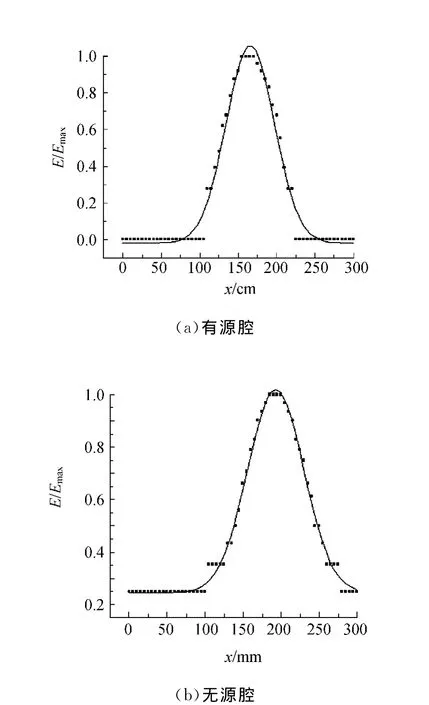
图9 腔内电场的相对分布曲线

我们搭建的装置与选用的测量参量仍存在一些可以改善之处.主要有以下几点：

1）品质因数的不确定度较大，例如有源腔的相对不确定度甚至达到了12.7%.应该进一步研究品质因数的测量方法及相应的不确定度的计算方法.

2）目前尚缺乏对有源腔的内部构造的了解，例如，腔体的内部很可能存在“鼻锥”结构，因此使用的探针长度具有一定不合理之处，从而对有源腔的谐振频率以及电场分布的测量可能造成一定影响.

3）尚不清楚对圆柱形谐振腔采用电耦合是否会带来误差.

5 结 论

搭建了测量同步辐射用无源和有源高频腔性能的实验平台，并且测量了谐振频率、品质因数以及中心轴线电场分布.测得有源腔谐振频率为（204.94±0.01）MHz，品质因数为（4.0±0.5）× 103；无源腔谐振频率为（1.584 3±0.000 1）GHz，品质因数为（8.4±0.2）×103；2个高频腔的电场在中心轴线上大致为高斯分布.在实验设计中，考虑了探针位置、微扰体大小及放置位置等因素对高频腔谐振频率、品质因素和腔内电场分布的影响.测量结果表明本文的实验设计及测量工作是合理的.

致谢：感谢复旦大学的乐永康、孙午炯、何琼、李爱萍，上海应用物理研究所的刘建飞、侯洪涛，以及合肥国家同步辐射实验室的董赛、李为民、黄贵荣等人的帮助和支持.感谢上海应用物理研究所和国家同步辐射实验室提供实验用高频腔以及复旦大学物理教学实验中心的优越实验条件.

张新夷教授的推荐：此工作利用上海光源和合肥光源2个同步辐射装置上的高频腔开展新物理实验的设计、搭建和测试，取得了成功，也拉近了本科生与大科学装置的距离，特此推荐此文.在此工作中，周航和徐杨作出相同的贡献.

［1］ 徐彭寿，潘国强.同步辐射应用基础［M］.合肥：中国科学技术大学出版社，2010：43－70.

［2］ 刘祖平.同步辐射光源物理引论［M］.合肥：中国科学技术大学出版社，2009：1－7，143－160.

［3］ 林芸，何正良.同步辐射用谐振腔性能测试平台设计与搭建实验报告［EB／OL］.http：／／phylab.fudan.edu.cn／doku.php？id＝exp：highfrequency.

［4］ 徐天昊.高频腔相关参数测量与分析－同步辐射光源相关装置研究［EB／OL］.http：／／phylab.fudan.edu.cn／doku.php？id＝exp：highfrequency.

［5］ 张磊，韦高，冯萍丽.一种测量微波高Q谐振腔品质因数的新方法［J］.测控技术，2006，25（12）：20－25.

［6］ Agilent Technologies Co.，Ltd..Technical specifications：Agilent Technologies PNA series network snalyzers E8361A／C［Z］.

Experiment to measure the performance parameters of radio－frequency cavities used in synchrotron radiation

ZHOU Hang，XU Yang，ZHANG Xin－yi
（Department of Physics，Fudan University，Shanghai 200433，China）

A platform for the measurement of the performance parameters of two radio－frequency cavities，provided by National Synchrotron Radiation Laboratory（NSRL）and Shanghai Synchrotron Radiation Facility（SSRF），was set up，respectively，among which one was a coppery active cavity，and the other was a superconductive passive cavity.Both cavities were put under measurement，and their resonance frequencies，quality factors and distributions of electric fields were measured.

radio－frequency cavity；resonance frequency；quality factor；distribution of electric field

O441.5

A

1005－4642（2012）11－0001－06

［责任编辑：任德香］

“第2届全国高等学校近代物理实验教学研讨会”论文

2012－05－07；修改日期：2012－09－04

周 航（1990－），男，福建永安人，复旦大学物理学系2009级本科生.

徐 杨（1991－），男，河南漯河人，复旦大学物理学系2009级本科生.

指导教师：张新夷（1942－），男，上海人，复旦大学物理学系教授，博士，主要研究方向为凝聚态物理和同步辐射应用.