基于UKF的光纤惯导误差在线估计*
王新国,李爱华,刘洁瑜,单 斌
(第二炮兵工程大学,西安 710025)
0 引言
星光/惯性复合制导是一种自主性制导方法,不易受干扰,隐蔽性好,得到了广泛的研究和应用。目前国内这种制导体制已有很多方案。在SINS误差分离中,不论是单星、双星还是星图匹配方案都存在着不足,即只能分离初始对准误差和陀螺常值漂移,不能分离惯导系统的安装误差和标度因数误差。文献[1]和文献[2]虽然给出了一种分离这些误差的方法,但由于一次转弹过程中存在的稳态误差和随机误差使得分离结果误差较大。针对此缺点,利用转弹思想,文中提出一种基于旋转弹体的误差分离最优估计技术,并根据国内星敏感器的动态性能,设计了导弹弹体的旋转方案,并在星敏感器不同的动态精度条件下进行了多次仿真验证。
1 基于星光观测的SINS误差分离与估计方法
1.1 光纤陀螺组合模型
光纤陀螺捷联惯导中,其主要漂移包括标度因数误差、零偏误差和安装误差,测试表明,即使温度不变时,零偏误差仍会发生缓慢变化,可采用一次模型来描述其变化:D0i(t)=ait+d0i,ai和d0i为零偏模型的一次项系数和零次项(i=x,y,z);由于在弹道导弹中,惯导工作时间较短,在线分离其误差时,可令ai=0,即认为零偏与时间无关,看作一个常值。
光纤陀螺组合补偿模型取如下形式:

将(1)式改写为:
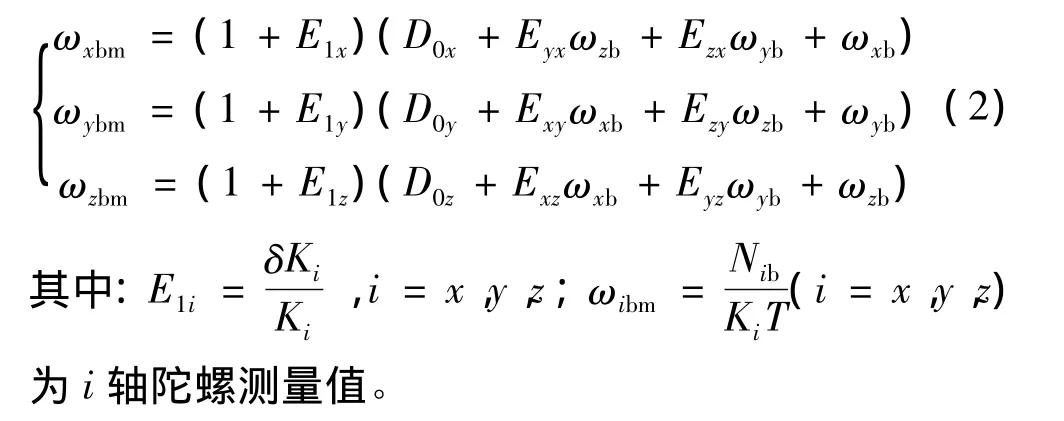
则由式(2),解得:
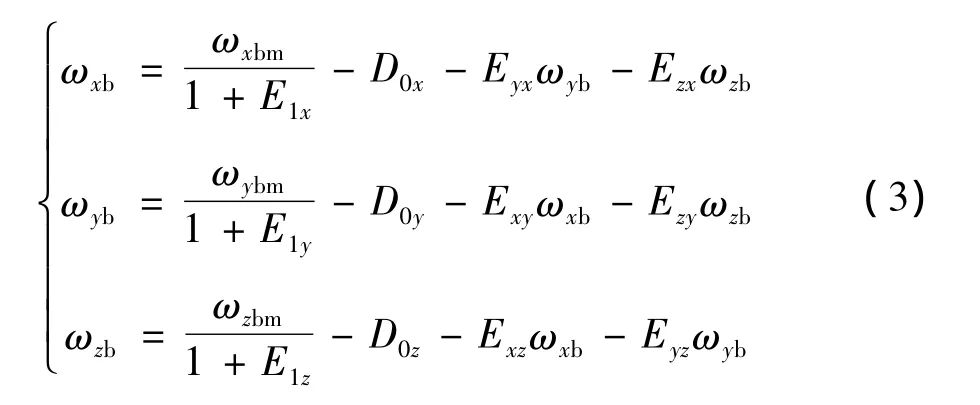
由于式(3)中各误差量均较小,采用近似解法,即忽略2阶小量,可直接采用测量值ωibm代替ωib得到:
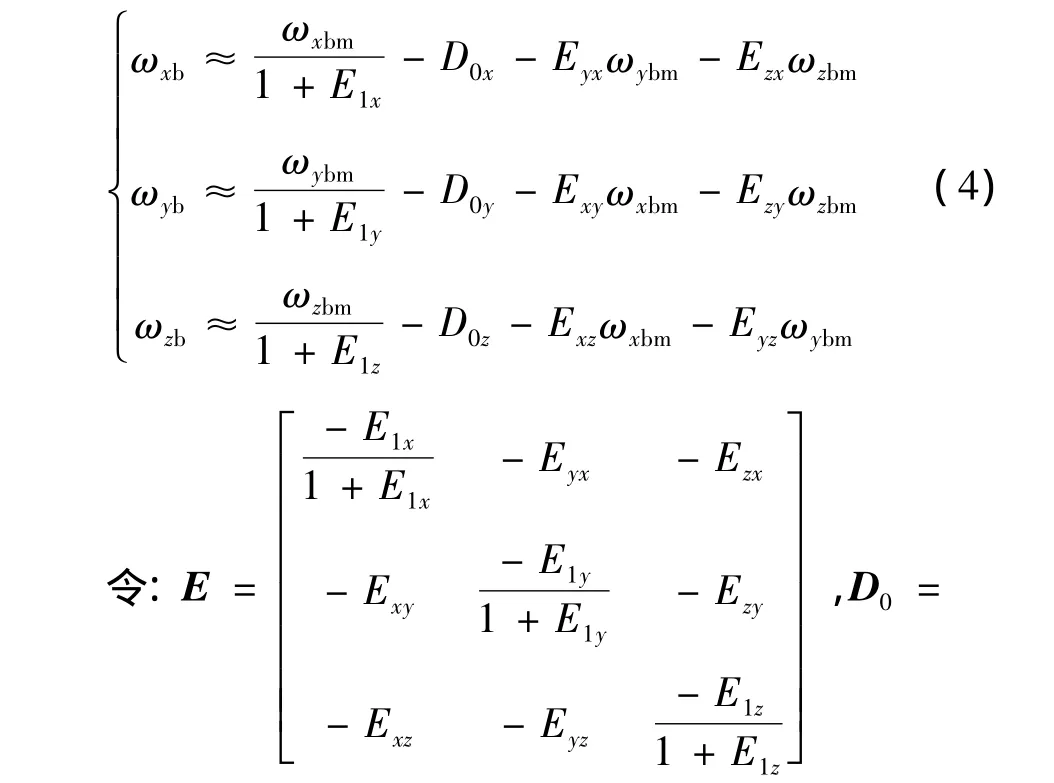
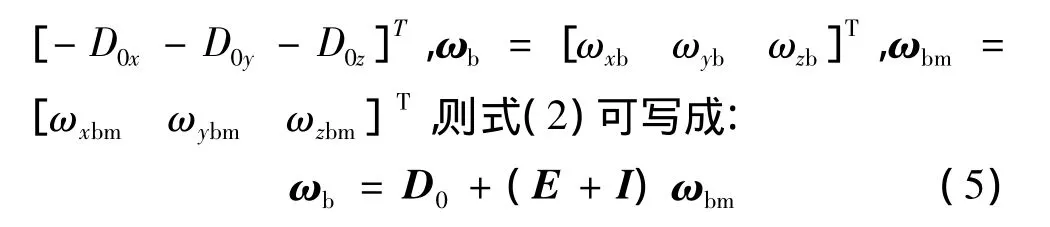
则陀螺误差表述为:
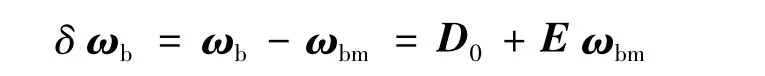
1.2 状态方程和测量方程设计
采用 Rodrigues参数[3]描述姿态运动,定义Rodrigues参数:R=[R1R2R3]T=tan(θ/2)e,式中的e和θ分别代表旋转轴和旋转角,R各分量独立,其取值范围是(-∞,+∞)。假设导弹的角运动是刚体角运动,可得其运动学方程为:
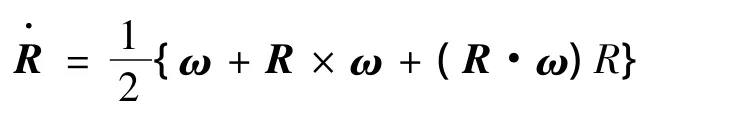
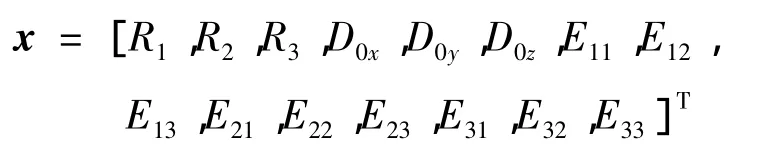
取系统状态向量为15维状态:设光纤陀螺常值漂移、标度因数误差和安装误差在陀螺启动之后均为常值,则系统状态方程为:
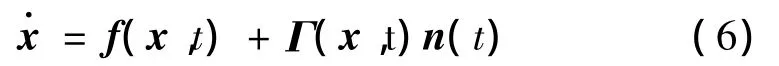
设n的统计特性如下:E[n(t)]=0,E[n(t)nT(t- τ)]=Q'(t)δ(t- τ),Q'(t)= σ2gI3×3。由此可知整个系统的过程噪声的均值为015×1,方差阵为:Q(t)= Γ(t)Q'(t)ΓT(t)。
根据星敏感器测得的星光向量,采用QUEST算法[4]进行处理,得到Rodrigues参数R的估值作为测量值,即可建立线性的测量方程:

1.3 不可观测状态的可观测化处理
上述系统不完全可观测,只能分离出初始对准误差和陀螺随机常值漂移。文献[1]和文献[2]证明了通过转弹激励,可以分段的分离出标度因数误差和安装误差等上述误差项,即此时系统每个状态虽然不是时时可观测的,但在整个转弹过程中所有状态都可观测。因此,上述估计算法若要估计出标度因数误差和安装误差,就需要进行转弹。
为避免Rodrigues参数出现奇异且保持一定的精度,设计转弹时,原则是无论俯仰、偏航还是滚动的角度都在现有姿态的±50°之内。转弹时,首先使导弹滚动,然后使之做俯仰运动,最后进行偏航运动。在导弹进行偏航和俯仰转动时,导弹会产生横向和法向运动,在转动时不启动横法向导引,在转动激励完成后,一次补偿前启动横法向导引控制。文中不再讨论转弹的姿态控制算法问题,下面的仿真假设转弹没有误差。实际上,转弹的姿态控制误差对系统没有太大影响,因为是利用星光观测来确定其姿态,转弹只是提供一个导弹姿态的机动,使系统变为可观测的。
转弹过程中,星敏感器动态性能是影响其姿态测量精度的主要因素[5-6]。目前国外星敏感器动态性能约为3°/s,最大可达10°/s,国内约为 3°/s。虽然提高星敏感器动态性能的方法不是文中探讨的内容,但为使文中研究更加符合动态环境,这里针对不同环境设置了不同的星敏感器姿态确定的精度,具体方案见下节仿真。
2 误差分离的UKF设计及仿真
该系统中,状态方程为非线性方程,因此最优估计应采用非线性滤波算法,最为常用的非线性滤波算法有 EKF、UKF、PF 等[7-9],由于 EKF 存在线性化误差,在非线性严重或噪声统计不准时容易发散,PF虽然没有EKF的上述缺点,但其算法运算速度慢,无法满足导航和制导要求,折中考虑,采用UKF算法[8],UKF过程如下:
1)设定缩放系数α(常取10-4<α<1),描述状态变量先验分布的系数b(高斯分布时,b=2),二阶缩放系数k1(取作0或3-n,对于高斯分布取3-n最优),在k时刻选取的sigma点和权值为:

2)计算状态一步预测的sigma点:
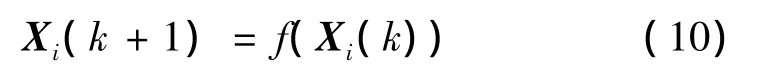
3)计算一步预测均值:
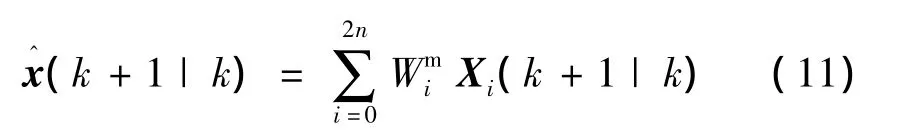
4)计算预测方差阵:
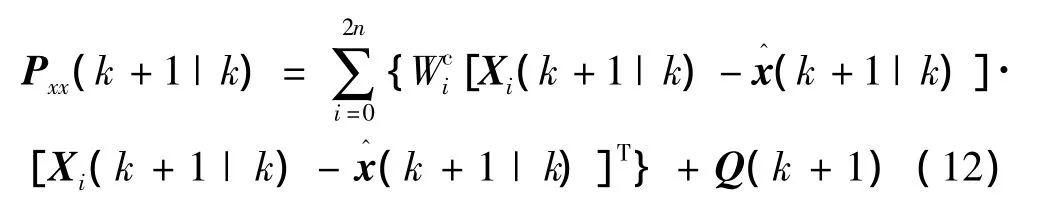
5)每个预测sigma点代入观测模型计算得:
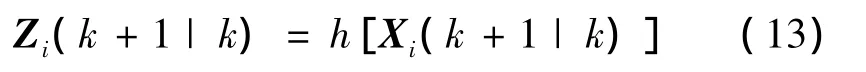
6)观测的预测值为:
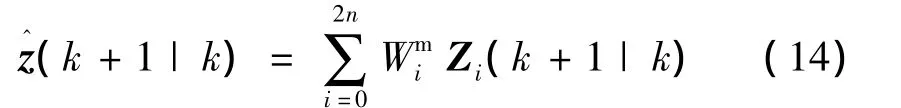
7)观测噪声方差阵:
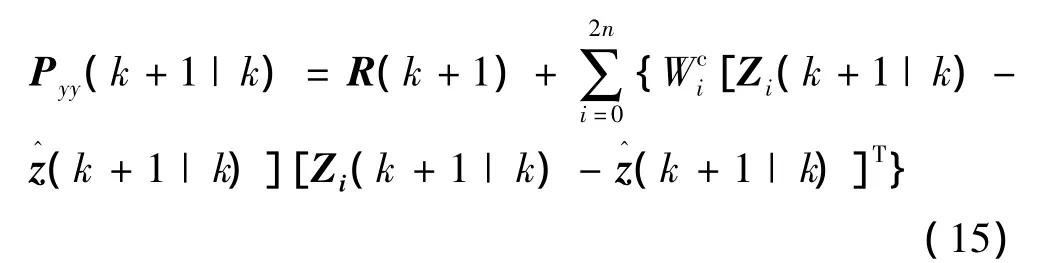
8)状态和量测的互相关阵为:
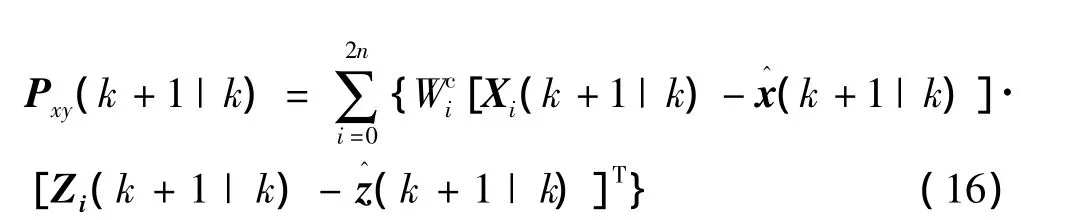
9)计算增益矩阵:
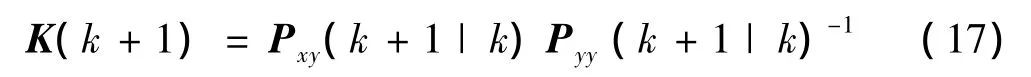
10)利用新息预报:
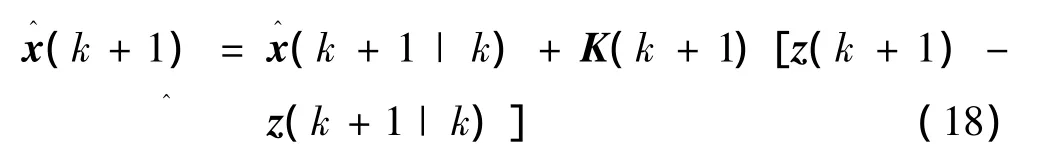
11)协方差推进:

为验证误差分离的效果,设计UKF仿真如下。设3 个陀螺零偏误差为 0.5°/h,随机误差 0.3°/h,标度因数和安装误差分别是:E1x=0.005,Eyx=0.01,Ezx=0.01,Exy=0.01,E1y=0.005,Ezy=0.01,Exz=0.01,Eyz=0.01,E1z=0.005,利用 1.1 节中 E 的表达式,可得:

在滤波时,估计E阵,然后根据E阵得到标度因数误差和安装误差。为充分激励误差,设计转弹过程如下:
1)第274s(主动段结束)启动星光观测,开始按照上述滤波方程进行滤波计算;
2)第284s启动滚动通道,以ωx=3°/s转动10s,接着以ωx=-3°/s转动10s;
3)第304s停转10s;
4)第314s启动俯仰通道以 ωz=3°/s转动10s,接着以ωz=-3°/s转动10s;
5)第334s停转10s;
6)第344s启动偏航通道,以ωy=3°/s转动10s,接着以ωy= -3°/s转动10s;
7)第364s,结束滤波计算。
为验证不同星光姿态确定精度下,零偏和E的估计效果,分别在星光姿态精度 σCNS为12″、60″和120″的条件下进行仿真验证。
σCNS为12″、60″和120″时的滤波结果如图1 ~图3所示,其中(a)图为3个陀螺零偏的估计,(b)图分别是E阵各元素的估计值,即代表了标度因数和安装误差。从图1~图3的(b)图中可看出:当启动滚动通道转动时,E11、E21、E31很快收敛;当启动俯仰通道转动后,E13、E23、E33很快收敛;当启动偏航通道转动后,E12、E22、E32很快收敛;当滤波时间结束时,E阵各元素均收敛到真值附近。当σCNS=12″时,陀螺零偏、标度因数和安装误差均能以很高的精度很快收敛到真值附近;σCNS=60″时,陀螺零偏、标度因数和安装误差也能收敛到真值附近,零偏收敛速度稍慢于σCNS=12″时的速度;σCNS=120″时,标度因数和安装误差仍能收敛到真值附近,其精度和收敛速度迅速下降,零偏已不能收敛到真值。
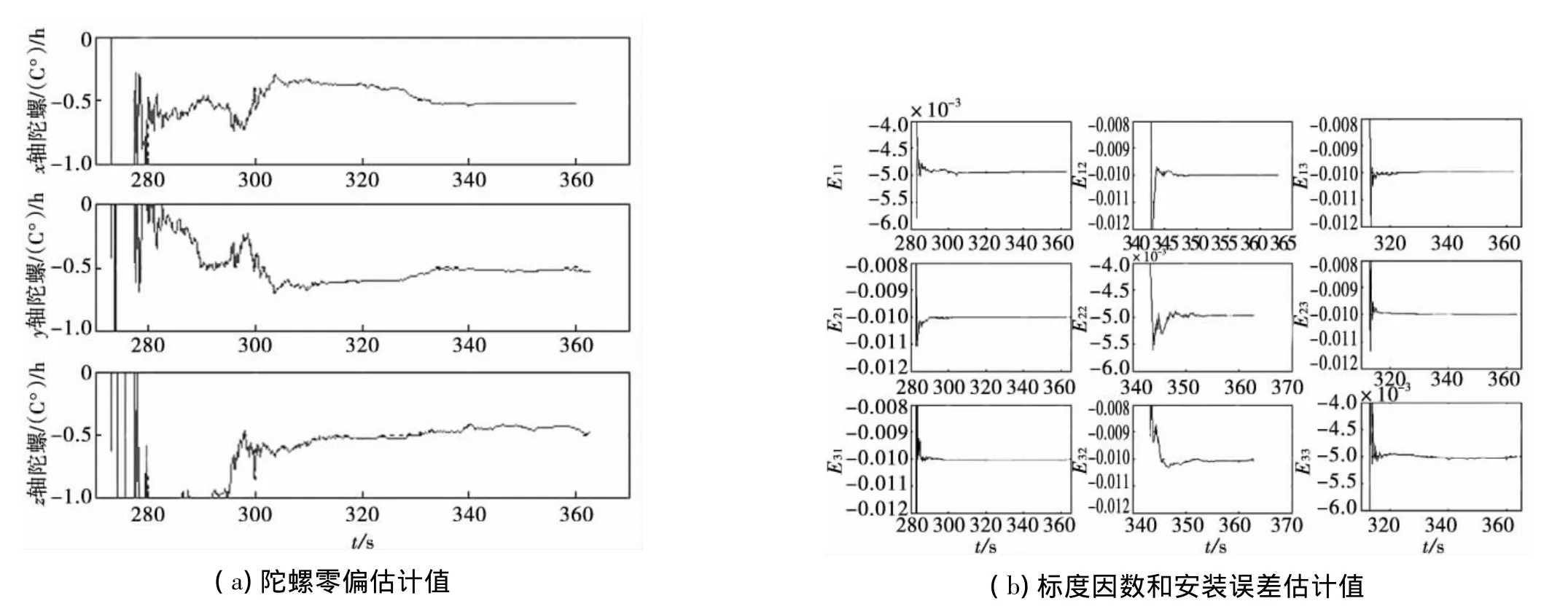
图1 σCNS=12″时的滤波结果
图2 σCNS=60″时的滤波结果
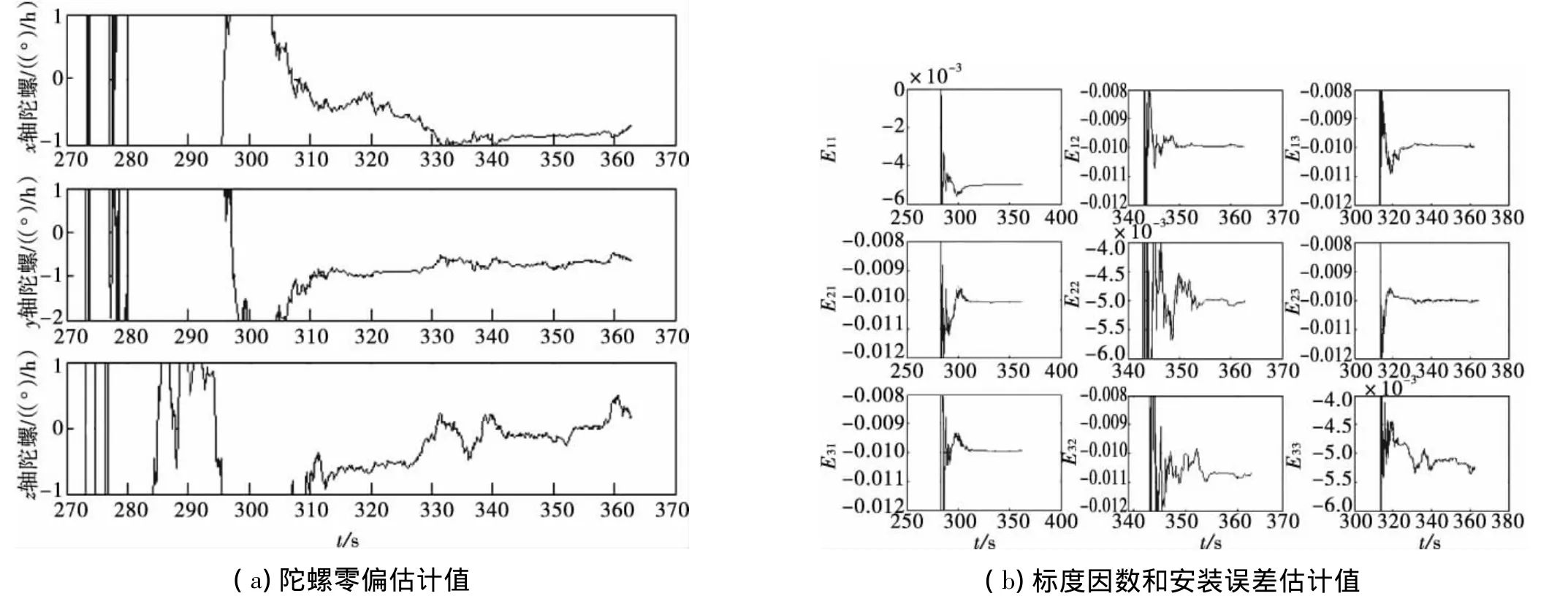
图3 σCNS=120″时的滤波结果
从上述仿真可以看出,陀螺零偏、标度因数和安装误差的估计效果与星光姿态确定精度有很大关系,在其星光姿态精度优于60″时,该系统具有很好的性能;同时可以看到,零偏收敛速度慢于E阵各元素收敛速度,而且零偏的估计精度比标度因数和安装误差对星光姿态动态测量精度更敏感。
3 结论
文中通过设计转弹方案实现了光纤陀螺捷联惯导全部状态的可观测,并设计了基于星光观测分离导弹光纤惯导误差系数的状态方程和观测方程,针对该方程设计了UKF滤波器,并在不同的星光姿态测量精度条件下进行了仿真,结果表明,在星光姿态精度优于60″时,该系统的全部状态均能较快的收敛到真值附近,但星光姿态精度差于120″时,陀螺零偏已不能收敛到真值了。这说明转弹和最优估计方案在星光动态姿态精度优于60″时,可比较精确的估计惯导更多误差系数。
[1]邵会兵,钱唯德,严卫钢.基于星敏感器的陀螺仪误差参数实时修正[J].现代防御技术,2006,34(1):33-36.
[2]贾大玲,李连仲,严卫钢.基于星敏感器的弹载陀螺工具误差分离研究[J].计算机仿真,2006,23(2):40-43.
[3]周江华,苗育红,王明海.姿态运动的Rodrigues参数描述[J].宇航学报,2004,25(5):514-519.
[4]MD Shuster.Algorithms for determining optimal attitude solutions,NASA-CR-183473[R].1978.
[5]郭贺,邓年茂,罗长洲.动态因素对星敏感器测星影响的分析[J].航天控制,2008,26(6):38-41.
[6]龚德铸,武延鹏,卢欣.一种提高星敏感器动态性能的方法[J].空间控制技术与应用,2009,35(6):19-23.
[7]Son-Goo Kim,John L Crassidis,Yang Cheng,et al.Kalman filtering for relative spacecraft attitude and position estimation[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit,2005.
[8]Simon JJulier.The scaled unscented transformation[C]//Proceedings of the 2002 American Control Conference,2002:4555-4559.
[9]Rudolph van der Merwe,Arnaud Doucet,Nando de Freitas,etal.The unscented particle filter[R].Technical Report CIED/F-INFENG/TR 380,Cambridge University Engineering Department,2000.
- 弹箭与制导学报的其它文章
- 攻角影响战斗部侵彻效应数值模拟分析*

