四节点矩形弹簧元及其特性研究

张青波，李世海，冯 春

（中国科学院力学研究所，北京 100190）

1 引 言

传统的数值计算方法将岩土体看作连续介质或者非连续介质，而忽略了岩土体宏观连续微观不连续的特点。有限元及有限差分方法的基础是连续介质力学，适用于模拟岩土体的连续变形及塑性破坏[1－2]。颗粒离散元法可方便地实现材料内部破坏，适合模拟微观尺度下材料的力学行为，但模拟连续介质时需对颗粒之间的弹簧进行复杂的标定[3－4]。刘晓宇等[5－6]构造了三维链网模型，给出了模型的几何与物理参数标定公式。

发展新型离散元模拟岩土体渐进破坏过程的研究取得了很大的进展。李世海等[7－9]提出的基于连续介质力学的离散单元法(CDEM)和张冲等[10－11]提出的三维简单变形体离散元方法(3SDEM)都是可以描述介质由连续到非连续的渐进破坏过程的数值计算方法。两种方法都可将块体看作简单变形体，在接触面上设置法向和切向弹簧，通过弹簧判断实现非连续计算。3SDEM 中接触弹簧刚度系数的选取具有人为性，CDEM法给出了接触弹簧刚度的计算公式。方明霁等[12－13]将块体离散为法向、剪切和扭转弹簧，构造了一种多弹簧梁柱单元模型。冯春等[14]将长方体单元离散为 12根弹簧，通过离散弹簧系统和传统有限元单元节点力的等效关系给出了弹簧刚度的表达式。Li Shihai等[15]构造了三角形和四面体弹簧元，对连续问题得到了与传统有限元等价的一组弹簧系统，该方法通过有限元的单元刚度矩阵标定各弹簧的刚度。

新型离散元方法在计算连续介质问题时的计算能力多等同于传统有限元中的常应变单元或者双线性单元，对提高单元计算精度的研究较少。但对某些常见问题（如梁的弯曲）这些单元的计算精度是很差的[16]。在有限元中（如Wilson非协调元等）构造各种形式的非协调元就是一种构造低阶高精度单元的有效手段[17]。

Li Shihai等[15]给出了一种对连续问题完全等价于相应有限元的弹簧系统，通过对比单元刚度矩阵得到各弹簧的刚度，其弹簧刚度的计算公式较其他几种方法更加合理。本文在此基础上发展了一种四节点矩形弹簧元，并求得了弹簧刚度的表达形式。通过改变弹簧刚度表达式中的系数可使该单元精度分别等同于常应变、双线性和Wilson非协调单元，极大地提高了弹簧元法求解连续问题时的计算精度。本文主要包含5个部分，下面分别进行阐述。

2 四节点矩形弹簧元的构成

考虑图1所示的四节点矩形单元，节点编号为1、2、3、4，节点坐标为单元长为 a，宽为 b。用 u表示X方向的位移，v表示Y方向的位移。

根据弹性力学理论[16]，四节点矩形单元的应变能表达式可写为

图1 四节点矩形单元Fig.1 Four-node rectangular element

式中：εx、εy、σx、σy为单元正应变和正应力；γxy、τxy为单元剪应变和剪应力；E为弹性模量；μ为泊松比；t为单元厚度。

弹簧元法是一种新型离散元，用离散系统描述连续介质力学行为是该方法的重要内容之一。与其他新型离散元方法不同，其核心思想是将单元看作一种结构，将单元应变能离散到一系列的弹簧上，用弹簧系统的刚度代替有限元的单元刚度描述单元节点力与节点位移之间的关系，使之在计算连续介质问题时与传统有限元完全等价。同时可以利用动态松弛方法等进行求解，避免传统有限元必须形成总体刚度矩阵带来的问题。

按照弹簧元的基本思想，将式（1）的应变能表达式写为求和形式，用弹簧的弹性势能替代单元的应变能，可得如下表达式：

式中：G为剪切模量；ai、bi为弹簧长度；ui、vi为弹簧弹性变形。

对图1所示的四节点矩形单元，将其离散为图2所示的四节点矩形弹簧元。

图2 四节点矩形弹簧元Fig.2 Four-node rectangular spring element

如图2所示，四节点矩形弹簧元由6个基本弹簧 s1、s2、s3、s4、s5、s6构成，其中弹簧 s1、s3、s5的法向沿X轴正向，s2、s4、s6的法向沿Y轴正向。图中A、B、C、D是4个插值点，其坐标值和位移值均由4个节点的坐标值和节点位移值进行线性插值得到，4个插值点位于各边的中点处。各基本弹簧的编号及弹簧首端编号和末端编号的对应关系见表1。

表1 基本弹簧编号及首末端对应关系Table 1 Relationships between the numbers ofbasic spring and its nodes

若设4个节点的位移分别为(ui，vi)(i=1, 2, 3, 4)，则6个基本弹簧的变形可由各弹簧两端点的相对位移求得，即第k个基本弹簧的两个方向的变形可表示为

式中：上标k =1, 2, 3, 4为弹簧编号；下标i为弹簧首端编号，下标j为弹簧末端编号。

k =5时

k =6时

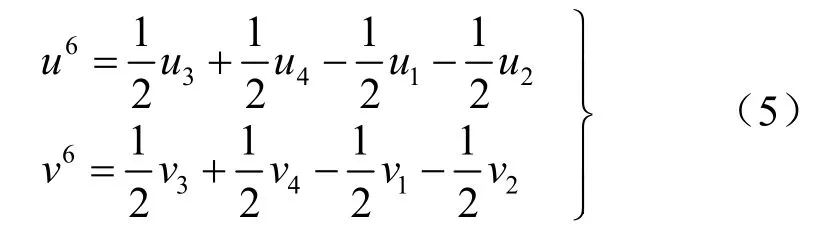
则矩形单元的应变能可由图2所示的6个基本弹簧的弹性势能表示为

式（6）中含 Ki的项等价于式（1）中含的项，含Gi的项等价于式(1)中含的项，故称Ki、Gi分别为弹簧si的法向和切向弹簧刚度系数。在式（6）中含KK的项等价于式（1）中含的项，含GG的项等价于式（1）中含的项，故称KK、GG分别为四节点矩形弹簧元的泊松弹簧和纯剪弹簧刚度系数。

3 弹簧刚度系数的确定

按照能量变分原理，式（6）表示的弹簧元应变能对节点位移求二次偏导数可得到弹簧元对应的单元刚度矩阵，其中

将有限元的形函数代入式（1）中并对节点位移求二次偏导数可得到有限元的单元刚度矩阵，其中

令

可以得到与四节点矩形有限单元对应的四节点矩形弹簧元中各弹簧的刚度系数表达式。式（10）给出了含待定系数的弹簧元刚度系数表达式。

式中：α、β为待定系数，其物理含义为单元应变能在各弹簧上的分配比例。

对任何一种确定的有限元形函数，都可通过式（9）得到相应的弹簧元的刚度系数表达形式。在有限元中可以通过给定含高阶项的形函数得到高精度的有限元解，同理，在弹簧元中也可以通过给定对应于含高阶项的形函数的待定系数，从而得到高精度的弹簧元解。对于四节点矩形单元，表2给出了有限元形函数为常应变非协调单元、双线性单元和Wilson非协调单元时，对应的四节点矩形弹簧元的刚度系数表达式中待定系数的取值。

表2 不同单元弹簧元刚度系数的取值Table 2 Coefficients in the stiffness expressions of springs with different elements

4 弹簧力、节点力的确定

由6个基本弹簧的变形及各弹簧的刚度系数可求得基本弹簧两个方向的弹簧力，其计算公式为

式中：i=1，2。

4个节点的节点力的计算公式为

式中：i =x，y。

5 算 例

将四节点矩形弹簧元与基于连续介质力学的离散单元法(CDEM)结合，形成了含四节点矩形弹簧元的计算程序。应用该程序计算了简单模型在简单载荷作用下的位移场，通过给定不同刚度系数，比较不同精度的单元对不同问题的适用性。

5.1 重力作用下块体位移场

重力作用是边坡稳定性分析的主要载荷。考虑一个100 m×100 m的块体在重力作用下的位移，计算模型如图3所示，通过给定不同的待定系数，用不同精度的单元计算A点Y方向的位移。材料的弹性模量 E =1 500 MPa，泊松比μ=0.25，密度ρ=2 g/cm3，计算结果如图4所示。

图3 计算模型Fig.3 Calculation model

图4 不同单元计算的A点位移与网格数(n×n)的关系Fig.4 Relationships between Y-displacement at point A and grid numbers (n×n)with different elements

从图中可以看出，对于计算重力载荷问题，双线性单元和 Willson非协调单元的计算精度相差不大，但常应变单元的计算精度相比较差，且块体划分为单数个网格时的结果比划分为偶数个网格时的结果好。

5.2 侧向线性压力下位移场

侧向线性压力载荷是土石坝、挡土墙稳定性分析中须考虑的重要载荷形式。如图 5所示一个100 m×100 m的块体，底部固定，左侧承受静水压力。通过给定不同的待定系数，用不同精度的单元计算 A点 X方向的位移，材料的弹性模量 E =1 500 MPa，泊松比μ=0.25，密度ρ=2 g/cm3，计算结果如图6所示。

从图中可以看出，对于计算静水压力问题，非线性单元和 Wilson非协调单元的计算精度相差不大，使用常应变单元计算时块体划分为偶数个网格时的结果比划分为奇数个网格时的结果好。

图5 计算模型Fig.5 Calculation model

5.3 悬臂梁算例

在工程结构中经常将问题简化为悬臂梁在自重作用下的挠度问题，考虑如图7所示悬臂梁：平面尺寸为10 m×2 m，梁左端固定，关注A点在重力作用下的挠度，计算结果如图 8、9所示。材料的弹性模量E=1 500 MPa，泊松比μ=0.25，密度ρ=2 g/cm3。

图7 计算模型Fig.7 Calculation model

从图8可以看出，悬臂梁的变形与理论解一致。从图9可以看出，对悬臂梁问题传统双线性单元的精度与常应变单元的精度都较差，而Wilson非协调元的精度较好，这与文献[16]中的结论一致，也从侧面验证了程序的可靠性。

图8 Wilson非协调元计算的位移 (网格数5×1)Fig.8 Displacement calculated by Wilson incompatible elements (with grid number of 5×1)

图9 不同单元计算的A点位移与网格数(5n×n)的关系Fig.9 Relationships between Y-displacement at point A and grid numbers(5n×n)with different elements

6 结 论

（1）将四节点矩形单元离散为6个基本弹簧，给出了一种四节点矩形弹簧元的构造形式。该单元的弹簧刚度表达形式、节点力公式简单，易于程序化，同传统有限元方法相比，可提高计算效率。

（2）通过改变弹簧刚度表达式中的待定系数可使该单元分别等价于常应变、双线性和Wilson非协调单元，表明该单元具有良好的扩展性，当待定系数取其他值时，可得到更高精度或者更低精度的结果。与其他新型离散元法相比，在计算连续介质问题时该单元具有更高的计算精度。

（3）不同算例表明：对重力作用下一般边坡的稳定性及侧向线性荷载作用下一般土石坝、挡土墙的稳定性问题可采用双线性及非协调元进行计算；对重力作用下一般悬臂梁的弯曲问题，应采用非协调元进行计算。

（4）本文研究了四节点矩形弹簧元的特性，对四节点任意四边形单元，可按类似的方法得到对应于双线性单元的离散弹簧刚度表达式，但对其特性的研究还有待深入。

[1]方建瑞, 许志雄, 庄晓营. 三维边坡稳定弹塑性有限元分析与评价[J]. 岩土力学, 2008, 29(10): 2667－2672.FANG Jian-rui, XU Zhi-xiong, ZHUANG Xiao-ying.Appraisal and analysis of three-dimensional slope stability based on elastoplastic FEM[J]. Rock and Soil Mechanics, 2008, 29(10): 2667－2672.

[2]戴自航, 刘志伟, 刘成禹, 等. 考虑张拉与剪切破坏的土坡稳定数值分析[J]. 岩石力学与工程学报, 2008,27(2): 375－382.DAI Zi-hang, LIU Zhi-wei, LIU Cheng-yu, et al.Numerical anslysis of soil slope stability considering tension and shear failures[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(2): 375－382.

[3]周健, 崔积弘, 贾敏才, 等. 静力触探试验的离散元数值模拟研究[J]. 岩土工程学报, 2007, 29(11): 1604－1610.ZHOU Jian, CUI Ji-hong, JIA Min-cai, et al. Numerical simulation of cone penetration test by discrete element method[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(11): 1604－1610.

[4]王桂萱, 秦建敏. 颗粒材料力学性质的离散元数值模拟[J]. 大连大学学报, 2007, 28(6): 27－31.WANG Gui-xuan, QIN Jian-min. Numerical simulation of mechanical behaviors of ellipsoid granular materials by discrete element method[J]. Journal of Dalian University, 2007, 28(6): 27－31.

[5]刘晓宇, 梁乃刚, 李敏. 三维链网模型及其参数标定[J].中国科学(A辑), 2002, 32(10): 887－894.LIU Xiao-yu, LIANG Nai-gang, LI Min. 3D network model and its parameter calibration[J]. Science in China(Ser. A), 2002, 32(10): 887－894.

[6]GUSEV A A. Finite element mapping for spring network representations of the mechanics of solids[J]. Physical Review Letter, 2004, 93(3): 1－4.

[7]LI Shi-hai, ZHAO Man-hong, WANG Yuan-nian, et al. A continuum-based discrete element method for continuous deformation and failure process[C]//WCCM VI in Conjunction with APCOM’04. Beijing: [s. n.], 2004.

[8]魏怀鹏, 易大可, 李世海, 等. 基于连续介质模型的离散元方法中弹簧性质研究[J]. 岩石力学与工程学报,2006, 25(6): 1159－1169.WEI Huai-peng, YI Da-ke, LI Shi-hai, et al. Study of spring properties of continuum-based discrete element method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(6): 1159－1169.

[9]田振农, 李世海, 刘晓宇, 等. 三维块体离散元可变形计算方法研究[J]. 岩石力学与工程学报, 2008, 27(增刊 1): 2832－2840.TIAN Zhen-nong, LI Shi-hai, LIU Xiao-yu, et al.Research on deformable calculation method based on three-dimensional block discrete element[J]. Chinese Journal of Rock Mechanics and Engineering, 2008,27(Supp. 1): 2832－2840.

[10]张冲, 金峰, 侯艳丽. 三维简单变形体离散元方法[J].岩土工程学报, 2007, 29(2): 159－163.ZHANG Chong, JIN Feng, HOU Yan-li. 3-D simple deformable distinct element method[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(2): 159－163.

[11]金峰, 胡卫, 张冲, 等. 考虑弹塑性本构的三维模态变形体离散元方法断裂模拟[J]. 工程力学, 2011, 28(5): 1－7.JIN Feng, HU Wei, ZHANG Chong, et al. A fracture simulation using 3-D mode distinct element method(3MDEM)with elastoplastic constitutive model[J].Engineering Mechanics, 2011, 28(5): 1－7.

[12]方明霁, 李国强, 孙飞飞, 等. 基于多弹簧模型的空间梁柱单元(I): 理论模型[J]. 计算力学学报, 2008, 25(1):129－133.FANG Ming-ji, LI Guo-qiang, SUN Fei-fei, et al.Multi-spring model beam element(I): Theoretical model[J]. Chinese Journal of Computational Mechanics, 2008, 25(1): 129－133.

[13]李国强, 方明霁, 孙飞飞, 等. 基于多弹簧模型的空间梁柱单元(II): 参数分析[J]. 计算力学学报, 2008, 25(1):134－138.LI Guo-qiang, FANG Ming-ji, SUN Fei-fei, et al.Multi-spring model beam element(II): Parameter analysisl[J]. Chinese Journal of Computational Mechanics, 2008, 25(1): 134－138.

[14]冯春, 李世海, 姚再兴. 基于连续介质力学的块体单元离散弹簧法研究[J]. 岩石力学与工程学报, 2010, 29(增刊 1): 2690－2705.FENG Chun, LI Shi-hai, YAO Zai-xing. Study of block-discrete-spring method based on continuum mechanics[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(Supp.1): 2690－2705.

[15]LI Shi-hai, ZHANG Ya-nan, FENG Chun. A spring system equivalent to continuum model[C]//Discrete Element Methods, Simulation of Discontinua：Theory and Applications. London: Queen Mary, University of London, 2010: 75－85.

[16]王勖成, 邵敏. 有限单元法基本原理和数值方法[M].北京: 清华大学出版社, 1996.

[17]任钧国, 熊龙飞. 低阶高精度单元的发展[J]. 国防科技大学学报, 1998, 20(4): 109－114.REN Jun-guo, XIONG Long-fei. Development of low order element with high accuracy[J]. Journal of National University of Defense Technology, 1998, 20(4): 109－114.