块体可动性判断的几何算法研究

徐栋栋，李 波

(长江科学院 水利部岩土力学与工程重点实验室，湖北 武汉 430010)

块体理论由石根华等在1985年首次提出[1]，是非连续变形分析方法[2]和数值流形法[3]的基础。块体理论本质上是一种几何分析方法，通过筛选几何上可动的块体，然后针对这一类块体展开稳定性分析，极大地提高了效率。目前，已经广泛应用于地下洞室、岩质边坡和坝基工程稳定性分析中。块体理论理论上非常完备，但针对某些假定的局限性以及工程实际需求，不少学者对其进行了改进。其发展主要有：①理论改进。如陈胜宏等[4]提出三维弹粘塑性块体理论，克服了传统块体理论未考虑力矩影响和结构面变形的缺陷。张子新等[5]建立了分形块体理论，并应用于三峡永久船闸高边坡岩体稳定性分析中，计算结果有效可靠。于青春等[6]提出一般块体理论方法，可解决任意大小裂隙、任意形状工程岩体的岩石块体识别及稳定性等计算问题，克服了无限大结构面假设、无法预测岩石块体数量和位置等缺点。邬爱清等[7]在三维结构面网络模拟的基础上，实现了三维随机块体的搜索工作。徐栋栋等[8]将块体理论扩展到地震历时作用下的动力稳定性分析中，以累积滑动位移和动安全系数共同评价块体的动力稳定性。②工程应用及改进。黄正加等[9]将块体理论中的矢量法成功地应用于三峡工程的随机块体及大型断层定位块体的稳定性分析中。张奇华等[10]将块体理论的应用在百色水利枢纽地下厂房岩体稳定性分析中进行了充分的展示。王在泉等[11]将块体理论应用于搜索岩质边坡的潜在滑移面。毛海和等[12]将其应用于龙滩水电站地下厂房洞室群工程稳定分析。杨庆等[13]将其应用于荒沟抽水蓄能电站地下厂房系统硐室群围岩稳定性分析中。邬爱清[14]将块体理论应用于三峡工程船闸边坡和地下厂房岩石块体稳定性分析中，解决了一系列关键问题，如任意形状的块体体积计算、凹形块体几何识别以及水压力计算等。③软件开发。张奇华等[15]在Windows环境下开发了块体理论的工程分析软件，具备完备工程分析所需功能，如赤平投影、复杂块体可视化、块体稳定性分析及支护措施、随机块体分析等。中国科学院大学工程计算中心也研发了easyKBT和VisKBT软件，具有较好交互界面。另外，李建勇等[16]综述了块体理论的发展历程，具有很好的参考价值。

工程岩体稳定性分析往往是在地质素描图的基础上展开的，第一步要找出不同结构面组合可能形成的可动块体。赤平投影分析方法因其直观性，受到了工程人员的青睐，实际上是一种纯几何分析方法。判断块体的有限性和可动性，实际上就是判断节理锥是否非空以及节理锥和开挖锥之间是否有交集。传统方法采用人为观测方式来判断，这一方式受主观因素影响较大。通过计算几何方式将这些节理锥或开挖锥以几何图形方式进行表征，进而通过其间的关系判断块体的可动性，可提高分析准确性和效率。

1 块体理论概述

裂隙岩体由空间不连续面切割而成，在自然状态下是静力平衡的。但当遭遇到人工扰动，如边坡或地下洞室开挖等，会使得暴露在临空面上的块体由于边界条件的解除而失去了原始平衡状态，产生剪切滑移或崩塌，甚至会产生连带效应，造成整个工程岩体的破坏。首先失稳的块体称之为关键块体。块体理论研究岩体结构被扰动后的破坏机制以及相应的工程处理措施。块体理论严格遵循3个基本假定：①不连续面为平面且无限大；②岩石块体为刚体；③岩体失稳为沿结构面的剪切滑移。

1.1 两个基本定理

块体的可动性判断是基于棱锥展开的。棱锥是将各组结构面和临空面移至一公共点后，构成的以此公共点为顶点的一系列空间区域。仅以结构面为界的岩体半空间所构成的棱锥称为节理锥(JP)；仅以临空面为界的岩体半空间所构成的棱锥称为开挖锥(EP)。块体的有限性及几何可动性定理如下：

1)块体的有限性定理：

一个凸形块体为有限的充要条件是，节理锥与开挖锥的交集为空集。即：

JP∩EP=Φ。

(1)

2)凸形块体几何可动性定理：

一个凸形块体，当其块体有限，且节理锥为非空集时，该块体为几何上的可动块体；当其块体有限，节理锥域也是空集，则块体为几何上的不可动块体。可动块体的充要条件用数学表达为：

(2)

1.2 全空间赤平投影

块体理论有两种分析方法：矢量运算法和全空间赤平投影方法。两者是相互独立的求解方法，这里仅针对全空间赤平投影这种几何分析方法展开，目的在于克服块体有限性判断时需要人为观测JP和EP几何包含关系的缺陷。全空间赤平投影是判断块体可动性的最为直观和简便的方法。空间不连续面的全空间赤平投影为一圆形，其内部相应于不连续面的上半空间，外部表示全部下半空间，两者组合在一起构成全空间。

如图1，赤平投影以球体作为投影工具(称为投影球)，将结构面或临空面平移使之置于球心，由球心发射射线将所有平面自球心开始投影于球面上，得到平面的球面投影。然后，再以投影球的南极或北极为发射点，将平面的球面投影再投影于赤道平面上。本研究采用的是下极射投影，也就是从球的南极点发射射线，如图2。

图1 投影球和投影圆

图2 投影原理

全空间赤平投影将三维岩体的空间属性以二维投影区域的方式表示，便于块体理论的工程应用。不连续面组成的不同类型的锥域可用全空间极射赤平投影平面上相应的投影区域表示；块体的有限性和几何可动性判断定理则是相应投影区域间的几何包含关系。

2 可动性判断的几何算法实现

以文献[17]中凹形边坡算例为例，对块体可动性判断的几何算法实现流程作说明，流程图如图3所示。采用MATLAB编程实现，该流程可以复现且难度不大。

图3 算法程序流程图

1)选用案例参数

边坡中有4组结构面P1～P4和2组临空面P5～P6，各个平面的产状如表1所示；是由P5的下盘L5和P6的上盘U6组成的凹形边坡。

表1 各个平面的产状

2)赤平投影圆的半径及圆心

直角坐标系下，赤平投影图以参照圆圆心为原点，正东为x向轴，正北为y向轴。设不连续面P的投影圆半径为r，倾角为α，倾向为β的平面，圆心坐标为Cx和Cy，则有：

(3)

其中，R表示参照球面的半径。

计算几何中，往往采用一系列短线段组合的方式来表征圆形，当线段长度足够短时可以逼近整圆，这与文献[1]块体理论相关程序中的处理保持一致。选用所有结构面和临空面投影圆中半径最小的圆的某个小角度所对应的弧长作为基准，对所有的圆进行离散。离散时所用角度可以根据计算需要进行调整，本研究选用5°离散线段表征结构面和临空面的投影圆，如图4所示。通过离散点以及交割点即可对JP和EP所代表的区域进行几何描述，类似于非连续变形分析方法中的“块体”。

图4 结构面和临空面的投影圆

3)无限区域的有限表征

根据下极射投影，不连续面的上盘为投影圆的内部区域，是一个有限区域；而下盘则是一个无限区域，这使得几何描述JP或EP区域变得不可能。但采用合适的有限区域表征这一无限区域即可将这一症结彻底解决。

具体做法为：针对所有的投影圆，确定一个初始矩形框，刚好将所有圆包含在内；然后将水平和竖直向外延一定的长度确定新的矩形框，如图5所示。确定所有圆的最小x坐标点和最大x坐标点，建立两条与矩形框相交的线段，使得矩形框与投影圆之间可以建立几何切割关系，便于后续对于JP或EP的几何特征的描述。至此，就形成了切割JP、EP系统以及表征上下盘关系所需要的所有线段的信息。下一步的工作就是进行拓扑切割，形成相关环路信息。

图5 表征结构面和临空面的几何系统

4)拓扑切割形成JP初始域

这里，参与切割的是结构面投影圆的相关线段以及补充的矩形框和两条线段，切割完后形成了表征不同JP的初始相关环路，如图6所示。实际上，两条辅助线段是为了规避切割程序对多连通域无法操作的缺陷而引入的，它们本不应存在。因此，对于共用两条辅助线段的相关区域的所有线段，在剔除这两条线段后，进行环路搜索，即将这些区域进行融合生成了最终的JP，如图7所示。环路搜索是一个较为复杂的拓扑操作，具体可参考文献[18]。

图6 形成的初步JP区域

图7 形成的最终JP区域

5)开挖锥区域

针对这一算例，开挖锥EP=L5∪U6，L5和U6区域如图8所示。换言之，表征P5的下盘区域和表征P6的上盘区域的并集为开挖锥EP的区域，如图9所示。表征L5的多边形为一多连通区域，U6为一单连通区域，两者求并已经有很多较为成熟的算法，这里不再赘述。

图8 P5的下盘和P6的上盘

图9 EP区域

6)确定节理锥编号

将每个JP区域依次与4个投影圆区域进行比较，若JP位于圆内，则JP区域处于上盘，记为0，否则是下盘，记为1，循环完后即可得到JP区域的编号，如图10所示。

图10 JP编号

7)确定JP区域与EP区域是否有交集

已知在JP非空的情况下，判断JP和EP是否具有交集，以便于判断块体的可动性。如图11所示，JP1100和1010与EP并无交集，说明块体是可动的。其余情况下，两者均有交集，说明块体为不可动块体。如图12所示，JP1011和1111中突出的三维展示部分为交集。

图11 可动块体的JP与EP几何关系展示

图12 不可动块体的JP和EP的几何关系展示

3 工程应用

针对某供水工程TBM开挖隧洞，基于现场实测结构面数据，通过统计学的方法对岩体结构参数进行了定量化的描述和分析。在此基础上，利用蒙特卡罗对未测绘段洞室进行了模拟，生成了相应的随机结构面。利用本研究的算法，对临近的可能形成可动块体的不同随机结构面的组合进行了排查。在确定几何可动块体后，进一步利用全空间赤平投影程序进行分析滑动模式及安全系数的计算。极大减轻了工程师肉眼观测的负担，节省了工作量，提高了分析效率。本研究只选取一套可能的随机面组合进行分析，共包含4组结构面和4组临空面，如表2所示。

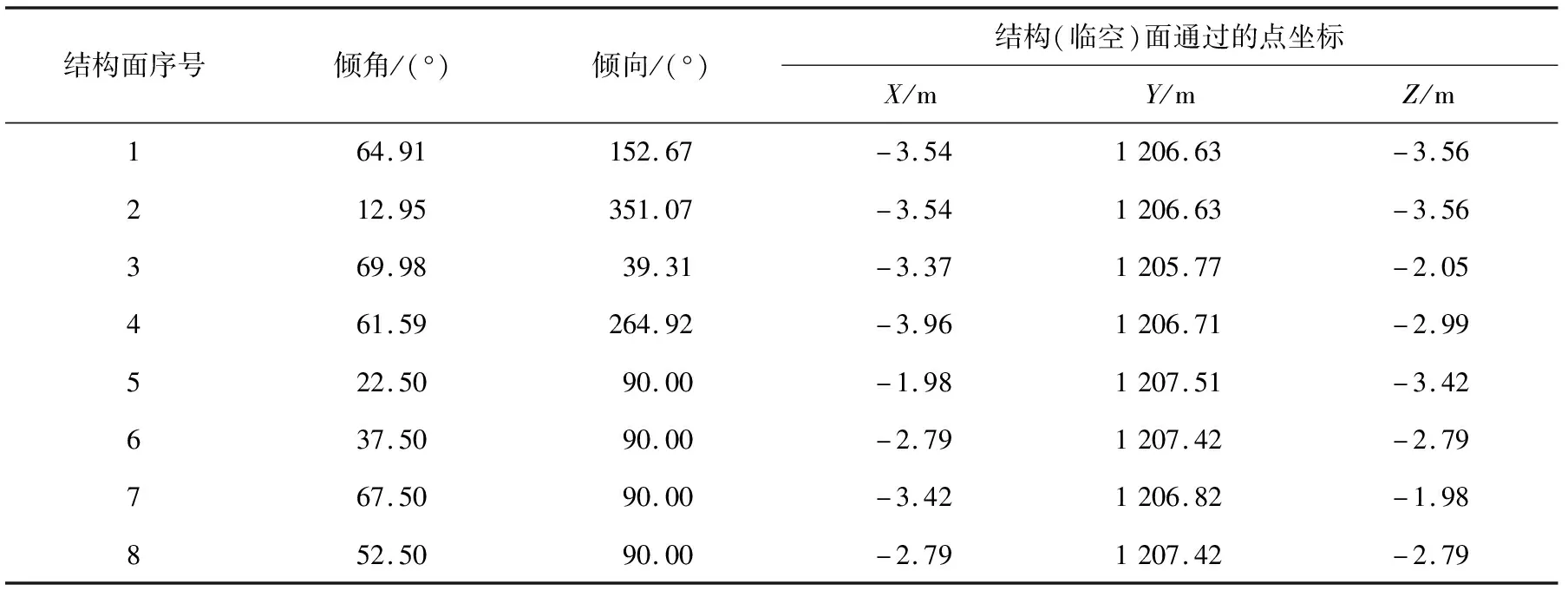
表2 结构面产状信息

利用本算法生成的节理锥如图13所示。JP0001和0011与EP并无交集，因此为几何可动块体，如图14～15。再进一步分析块体力学上的稳定性，如图16所示全空间赤平投影分析结果，可见0011在自重作用下是稳定的；而0001的滑动模式为沿着1、2面滑动，但在给定的摩擦角33°情况下，也是力学上稳定的。块体0001的形态如图17所示，体积为1.64 m3。

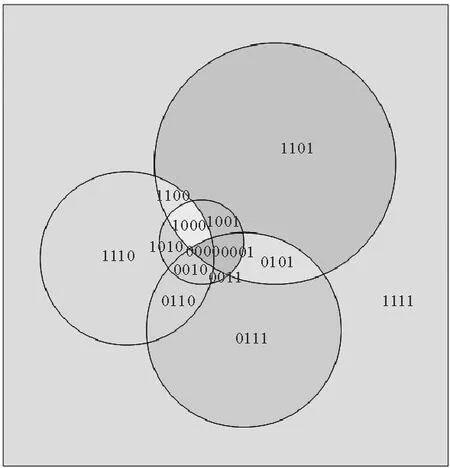
图13 不同区域代表的节理锥编号

图14 JP 0001与EP的几何关系

图15 JP 0011与EP的几何关系

图16 全空间赤平投影分析

图17 块体形态

4 结论

矢量分析方法可以独立实现块体可动性的判断，但其矩阵运算较为抽象，无法感性地认知JP和EP。全空间赤平投影的最大的优点在于直观，本研究针对可动性判断中块体是否有限需要人为判断这一缺陷进行了改进，以表征JP和EP的多边形之间是否存在重叠区域来确定两者之间的包含关系，可通过计算几何实现自动判断。这一套方法从几何上判断可动性是完备的，与矢量法是两种处理方式，相互独立。通过改进的算法进行第一步的筛选工作，有助快速通过纯几何的方法来获得几何可动的块体。在此基础上开展力学分析，可极大地提高分析效率。