盐岩储气库运营期失效概率分析研究

贾 超，李 朋，张强勇，李术才

（山东大学 土建与水利学院，济南 250061）

1 引 言

盐岩地下储气库具有存量大、调节范围广、安全可靠、经久耐用、运行成本低等优点，是大型输气干线系统配套不可缺少的重要组成部分[1]。随着我国“西气东输”工程的进行，以及对油气资源日益增长的市场需求，我国将会有越来越多的盐岩储气库建成并投入使用，以中石油为例，十二五规划期间，中石油将新建10座储气库，用以防范未来气荒和提高天然气调峰能力，因此，对盐岩储气库运行期的安全稳定性研究将成为未来盐岩地下储气库研究的重中之重。另外，盐岩地下储气库可有效地解决城市季节性调峰问题，在储气库正常运行期间，将根据市场需求，进行注、采天然气，储气库腔体内压将随时间而不断变化，而腔体内压对储气库的安全稳定有重要影响，因此，为准确研究储气库正常运行期的安全稳定性，应建立内压-时间历程函数曲线以描述内压随时间的变化，进而研究储气内压与储库安全稳定性之间的关系。同时，盐岩层多位于地下1 km深的位置，而且不同于国外盐丘型盐岩层，我国盐岩层具有层数多、单层厚度薄、含盐岩地层的不可溶解性夹层多的特点[2]，不确定性因素众多，因此，期望以定量数据准确描述出盐岩地下储气库整体体系的岩石力学性质的方法有待改进。以概率为基础的随机分析方法是解决不确定性问题的有力工具，所以，可将盐岩层岩石力学参数视为服从某分布的随机变量，基于随机力学的方法对其进行研究。

鉴于此，本文应用大型有限元分析软件ANSYS，建立了储气库数值模型，并应用其瞬态分析和可靠性分析模块，研究了随机不确定因素影响下，储气库在整个运营期失效概率的变化规律，并探讨了运营期注采气速率的变化对腔体应力状态和体积收缩的影响。

2 基于ANSYS瞬态分析的盐岩储气库运营期稳定性分析方法

ANSYS瞬态力学分析（亦称荷载-时间历程分析）是用于确定承受任意的随时间变化荷载的结构的力学响应的一种方法，可以用瞬态力学分析确定结构在静荷载、瞬态荷载和简谐荷载的随意组合作用下随时间变化的位移、应变、应力状态[3]；另一方面，盐岩储气库作为调峰工程，其工作内压随时间而不断变化，因此，在对储气库进行长期流变分析时，应将储气内压视为随时间变化的动荷载施加于腔体内表面。基于以上两点，本文采用 ANSYS瞬态力学分析方法，对盐岩储气库长期流变进行数值模拟。

2.1 腔体内压-时间历程荷载曲线的建立

以金坛盐岩储气库为例，储气库运行分为4个阶段[4]：恒定低压阶段、加压注气阶段、恒定高压阶段和降压采气阶段，腔体初始压力为7 MPa，每年3月份开始注气，6月份达到14 MPa后稳定3个月，然后开始采气，12月份降至最低工作内压7 MPa。为计算方便，本文以当年第1.5个月开始至次年第1.5个月结束为一周期，如图1所示。

基于上述假定，可在ANSYS中利用矩阵参数法建立与上述荷载相对应的荷载-时间数组，如图2所示。时间周期为1 a，ANSYS长期流变计算以h为单位，根据ANSYS单位制规定，输入压强数据单位为MPa。

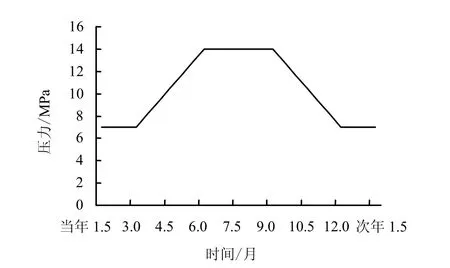
图1 计算选取的一周期内储气内压变化示意图Fig.1 Gas pressure curve in a cycle time for calculation

图2 一周期内荷载-时间数组Fig.2 Pressure-time array in a cycle time

2.2 盐岩本构模型的选取

与静力学分析相同，ANSYS瞬态时程分析同样需要对储气库模型进行非线性设置。

盐岩具有较强的蠕变能力，低渗透性和损伤自愈合性，因此，其力学特性比较复杂，杨春和等[5－7]已对其做了大量的研究工作。在储气库正常运行期间，盐岩体的长期流变特性将是影响盐岩储库安全稳定的重要因素。盐岩流变行为与盐岩承受的温度、应力状态和应变速率密切相关，研究表明，从长远来看，即使在非常小的偏应力作用下，盐岩也具有流变特性，盐岩的流变速率是偏应力和温度高阶非线性函数。因此，只要溶腔应力存在差值，终将慢慢收缩，从而导致腔体压力的升高[8]。

基于以上性质，在深部盐岩体中造腔，必然引起围岩在高地应力条件下的长期流变变形，本文采用符合盐岩流变的幂指数本构模型对正常运行期储气库进行长期流变变形分析，本构方程为

根据文献[6]中金坛盐矿蠕变试验的结果，参考国外储气库计算所采用的参数及国内部分深层钻井盐膏岩反演计算的盐岩蠕变参数，在本文算例中，确定盐岩蠕变参数如下：A0=6.0×10-6，n =3.5。

泥岩采用经典Maxwell流变本构模型。它是由虎克体（弹簧）和牛顿体（阻尼器）串联而成[9]，如图3所示。

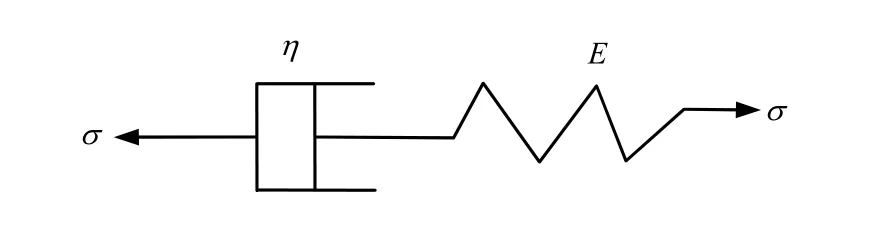
图3 马克斯韦尔模型Fig.3 Maxwell model

其本构方程为

式中：E为弹性模量；η为黏性模量。

3 基于ANSYS-PDS的储气库运营期失效概率分析方法

3.1 功能函数的确定

盐岩具有较强的流变特性，而流变特性具有时间依赖性，因此，在盐岩长期时效和不确定性分析中，应视其为随机过程，这种包括时间因素在内的结构可靠性模型称为时变可靠性模型。

在工程结构可靠性分析中，结构的极限状态一般由功能函数加以描述。当结构有m个随机变量影响结构的可靠度时，结构的功能函数为

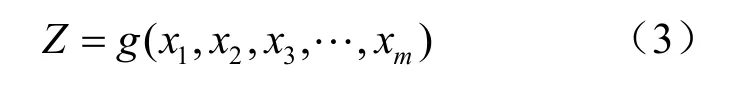
式中：xi（i=1, 2, 3,……, m）为m个随机变量。

在工程分析中，功能函数仅与荷载效应 S（内力、位移等）和抗力R（极限强度）两个随机变量有关，即结构功能函数可用其承载能力的大小来表示[10]：

式中：R(t)为结构抗力随机过程；S(t)为结构荷载随机过程，为结构中1个荷载或多个荷载的线性或非线性函数。

对应的极限状态方程为

设计基准期内结构的失效概率为

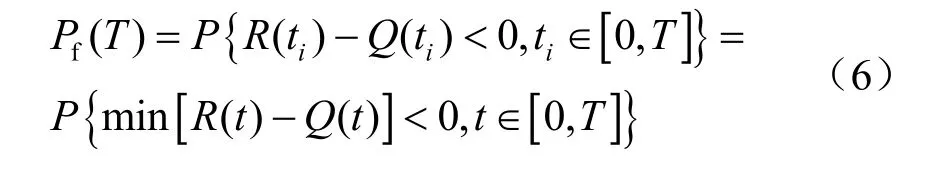
由于盐岩储气库为地下腔体结构体系，且具有较强的流变性和损伤自愈合性，因此，很难从材料力学的角度准确构造出其功能函数。本文结合相关研究[11]，确定将体积收缩作为评判其失效概率的依据。具体来说，根据盐岩蠕变性质，在储气库长期运行期间，由于溶腔应力存在差值，在长期周期性内压作用下，腔体终将慢慢收缩；当体积收缩率到一定限值后，将严重影响其整体稳定性，并导致天然气储存效率的下降，记该限值为w，则功能函数可表示为

对应的极限状态方程为

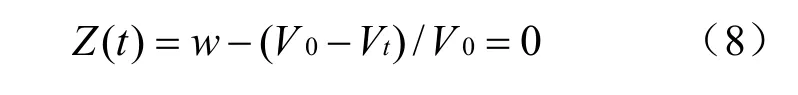
式中：V0为腔体初始体积；Vt为正常运行t a后腔体的体积。

我国地下储气库建设尚处于初步阶段，关于地下储库的研究，尤其是在其可靠性及风险分析方面研究较少。国际上一般认为，当收缩率达到某限值时，储气库将进入破坏阶段，本文参考相关文献[6，11]，选取0.3作为体积收缩限值。

3.2 时变失效概率分析方法的实现

ANSYS软件本身不能进行时变可靠性分析，本文假设储气库正常运行期间储气内压每年随时间变化相同，根据储气库运行1 a期间内压-时间曲线（见图2），可得出储气库运行t a（t =1，2，…，30）的储气内压-时间历程曲线，图4为储气库运行10 a，内压-时间历程曲线。利用ANSYS APDL语言编制循环子程序，分别将上述储气内压-时间历程曲线作为加载条件施加于储气库模型进行力学分析，并提取溶腔体积收缩量；视盐岩力学参数为随机变量，利用ANSYS-PDS模块中的蒙特卡洛方法，对瞬态力学分析结果分别进行可靠性分析，便可得到储气库运行t a后的失效概率Pt（t≥1），由此便可得出储气库在整个运营期失效概率的变化规律。整个过程作为离散随机过程。离散随机过程的时间因素通过在分析中取不同的时间t体现，不同时间下的计算结果在蒙特卡罗抽样计算中会得到不同的结果（不同的失效概率），这体现了随机过程研究对象的状态随时间的变化。由于储气库数值模型较为复杂，理论认为，计算次数一般应为1/Pf（Pf为储气库失效概率），为兼顾计算精度和工作效率，在用蒙特卡洛方法进行抽样计算时，本文取抽样次数为50 000次，相当于失效概率为0.002%，一般储气库的失效概率均大于该值，因此，抽样次数选取50 000次完全可以满足精度要求。

调控装置中叶片及主体框架是关键部件，其受风压及外力载荷影响，需要进行结构有限元安全性分析。叶片结构初始参数如下：20片叶片，长度400 mm，厚度1 mm，质量18.4 kg。主体框架结构初始参数如下：前圈厚度10 mm；框架直径1 000 mm；十字加强筋宽度5 mm。关键部件结构应力分析结果如图6所示。

图4 储气库运行10 a内压-时间历程曲线示意图Fig.4 Ten years’ pressure-time curve of the gas storage in operation period

4 金坛盐岩储气库数值模拟算例

4.1 数值模型的建立和材料参数的选取

根据金坛盐岩储气库的工程地质条件，参考文献[6]，建立三维分析模型，如图 5、6所示。计算区域设定为长方体，纵剖面包括 203.81 m厚盐岩层，盐岩层上、下各取300 m厚的泥岩层，计算剖面厚度共计803.81 m，底面积为800 m×800 m，库型选择椭球型腔体，长半轴长为75 m，短半轴长为32.142 8 m，长短轴比为 7/3，腔体体积为 32.46×104m3。由于模型对称，仅取1/4部分进行计算。根据相关资料[6]，盐岩、泥岩的材料力学参数见表1。单元类型采用四面体单元和六面体单元。

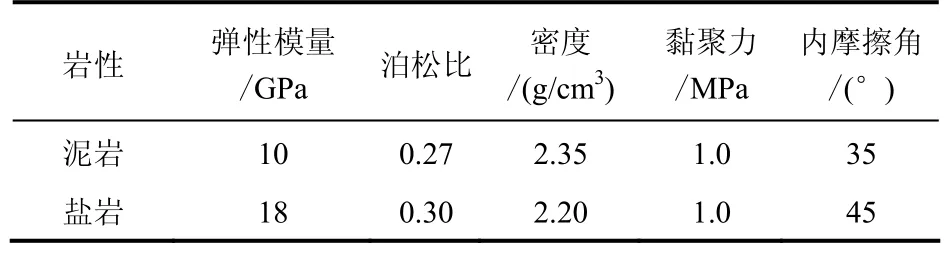
表1 地层基本参数Table 1 Basic parameters of strata

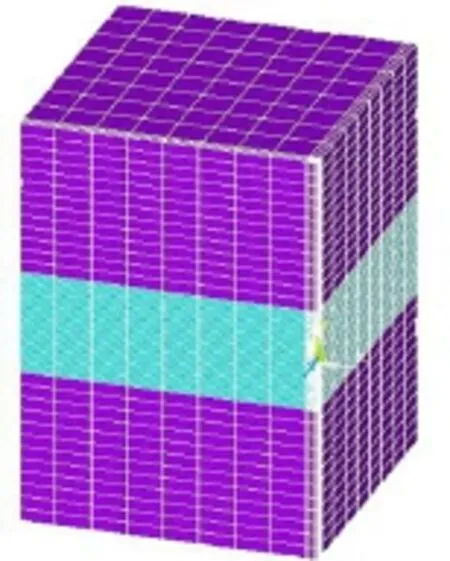
图5 有限元模型Fig.5 Finite element model

图6 腔体局部放大图Fig.6 Partial enlarged view of cavity

根据金坛盐岩储库介质材料的400组相似试块室内物理力学试验的结果[12－13]进行统计分析，储库介质力学参数近似服从正态分布；同时，在一段相对稳定的运营期内假定模型顶部压力近似服从均匀分布。储气库可靠性计算随机变量及分布特性参数取值见表2。

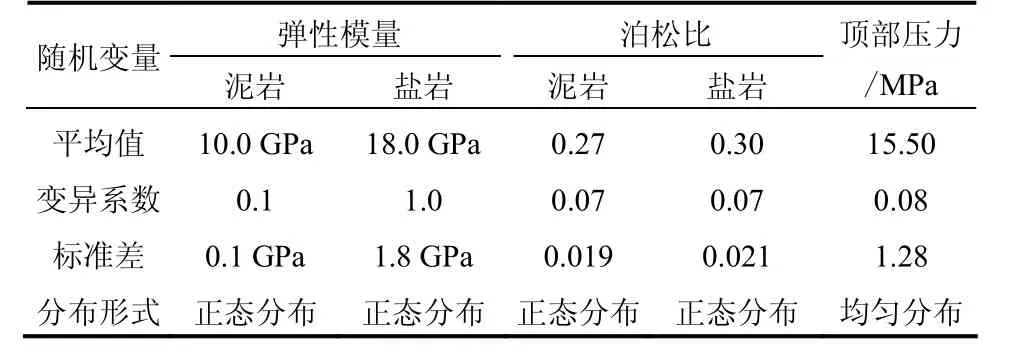
表2 储气库可靠性计算随机变量及分布特性参数Table 2 Input stochastic variables and distribution parameters for gas storage

4.2 边界条件的设定

有限元模型下表面用Y向简支约束，4纵表面受垂直于表面的法向简支约束，上覆岩层的重量简化为长方体模型的上表面的荷载，根据地层实际厚度及地层平均密度计算得等效荷载为15.5 MPa。为简单起见，在模拟岩体初始地应力时，本文忽略岩体的构造应力，只考虑其自重应力。由于建造储气库时自重应力早已完成作用，在数值模拟中，设定其结束时间为一极小值，本文取0.01 s。自重应力计算结束后，将荷载-时间历程曲线分别作为储气内压的变化曲线施加于腔体内表面，最后将所得到的位移结果减去初始位移场，即得储库正常运行期间腔体位移场。

4.3 计算结果分析

首先计算岩体初始地应力，然后计算在周期性腔体内压作用下腔体围岩位移、应力的时空响应，最后在介质力学参数服从某种分布随机取值的情况下，以式（8）作为失效函数计算储气库在特定时间点的时变失效概率。

图7、8为储气库分别运行1 a、10 a后腔体周围竖直方向位移云图；图9～11为储气库分别运行1 a、10 a、30 a期间腔体顶部Y向位移随时间的变化曲线。由图7、8可知，椭球形腔体在长期周期性荷载作用下，围岩将发生流变，流变主要发生在顶部和底部，运行10 a后，最大位移发生在腔体顶部。

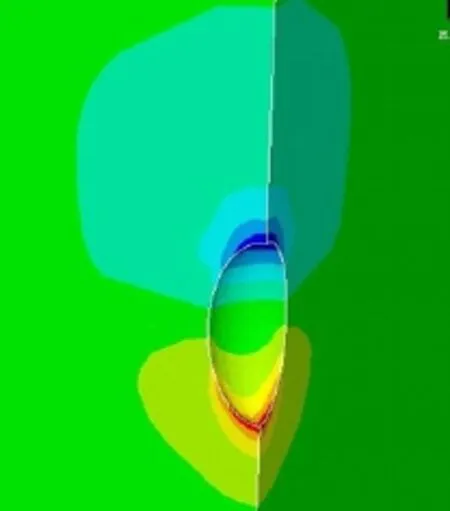
图7 运行1 a后腔体周围Y向位移云图Fig.7 One year’s nephogram of displacements in Y-direction during operation period

图8 运行10 a后腔体周围Y向位移云图Fig.8 Ten years’ nephogram of displacements in Y-direction during operation period

图9 运行1 a期腔体顶部位移随时间变化曲线Fig.9 One year’s displacement-time curve in y-direction during operation period

图10 运行10 a期腔体顶部位移随时间变化曲线Fig.10 Ten years’ displacement-time curve in y-direction during operation period

图11 运行30 a期腔体顶部位移随时间变化曲线Fig.11 Thirty years’ displacement-time curve in y-direction during operation period

由图9可知，储气库运行1 a期内，在初始低压运行阶段，腔体顶部节点位移迅速增加，随着注气工作的进行，储气内压不断增大，节点位移继续增大，但速度有所放缓，进入采气阶段，位移增加速度又逐渐增大；位移变化速率与荷载变化速率关系密切。由图10、11可知，在储气库长期运行过程中，腔体顶部节点位移-时间曲线呈波浪形逐渐下降，且随着时间的增加，腔体内压的周期性变化对腔体顶部节点位移变化速率的影响逐渐减弱。

表3为储气库运行N（N =1，2，…，30）a后的失效概率的统计（置信度为95%）。

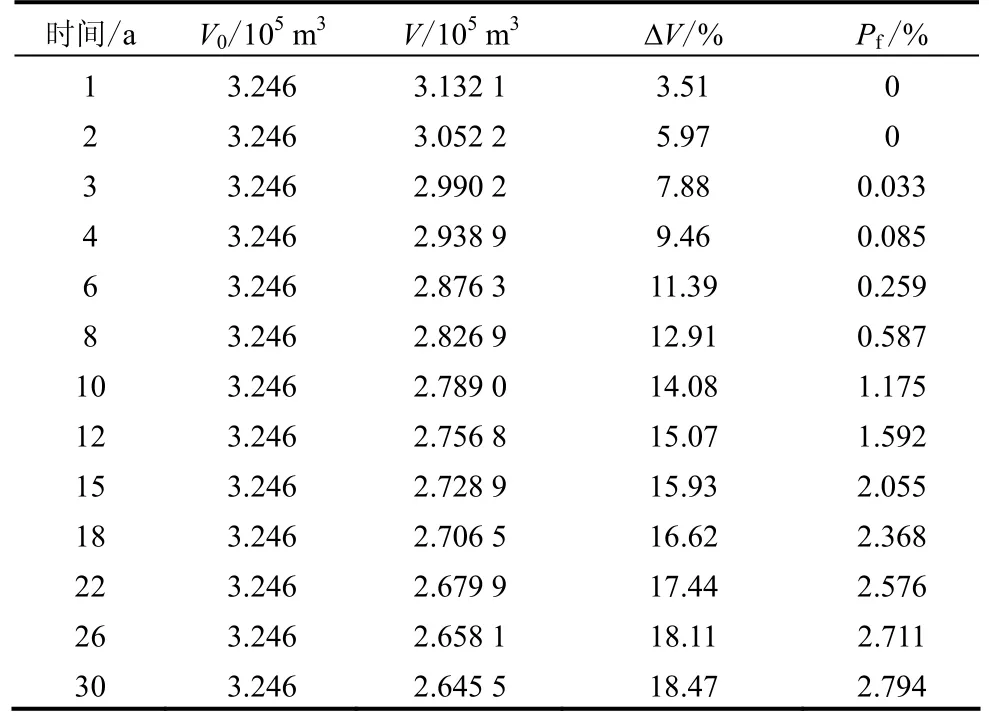
表3 储库失效概率统计表Table 3 Failure probability results of the gas storage

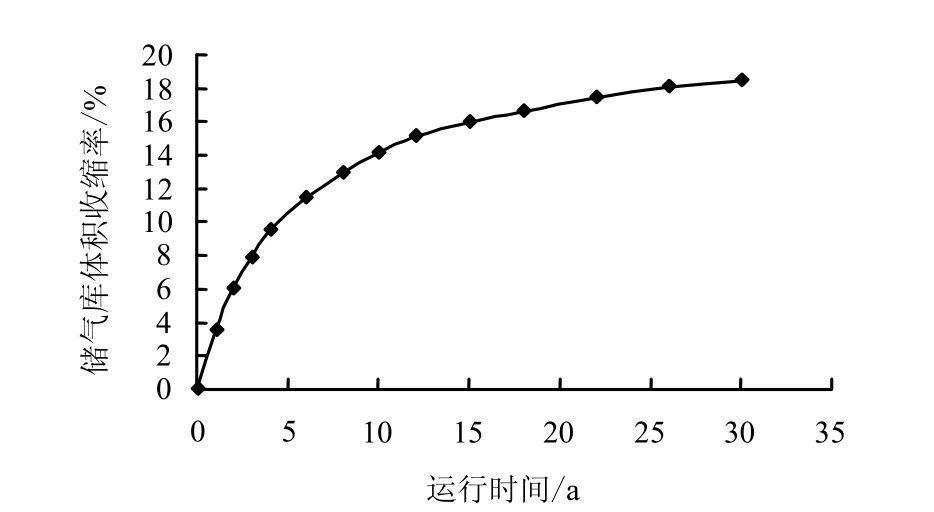
图12 储气库体积收缩率变化曲线Fig.12 Relationship between volumetric shrinkage and operating time

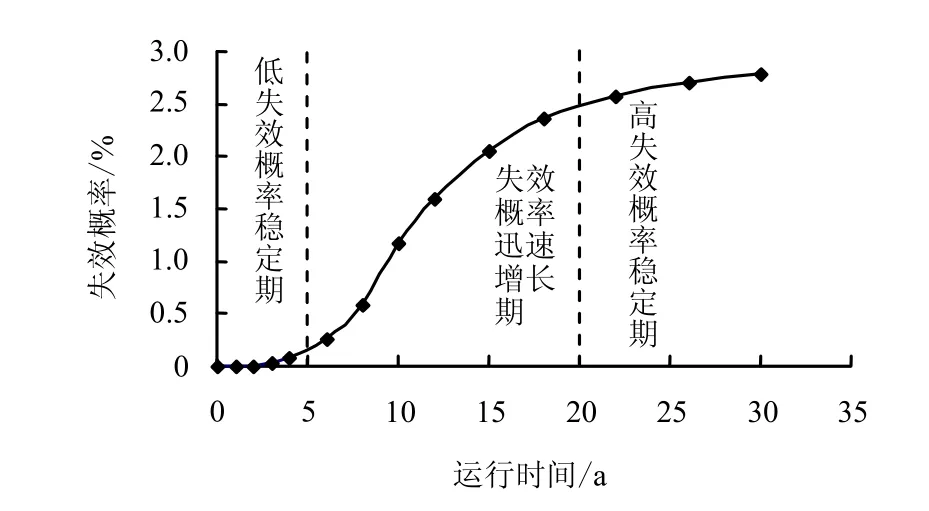
图13 储气库失效概率随时间的变化曲线Fig.13 Relationship between failure probability and operating time

由上述统计结果可知，在储气库运行期间，随着流变时间的增加，腔体体积不断缩小，运行初期，体积收缩速率较快，之后，体积收缩曲线逐渐趋于平缓。由图13可知，在储气库运行初期（0～5 a），储气库失效概率极低，可视为低失效概率稳定期；随着体积收缩率的不断增大，5～20 a间在以式（8）为失效函数的计算过程中，失效概率迅速增加，为失效概率迅速增长期；最后，由于体积收缩率变化不断减小，失效概率曲线趋于平缓，储库运行20 a以后为高失效概率稳定期。据以上分析可知，在储气库正常运行期的5～10 a间，对其进行维修加固，将有效抑制失效概率的迅速增大。

另外，储气库正常运行期间，因市场需求不稳定，天然气等能源的使用具有不均衡性，每次注采气速率不可能为一恒定值[14]。本文通过改变荷载-时间历程曲线，探讨了正常运行期间注采气速率对储气库稳定的影响。

图14为不同注采气速率下的荷载-时间历程曲线。注采速率分别为0.077 8、0.058 3、0.116 7 MPa/d。

图14 3种注采速率下的荷载-时间历程曲线Fig.14 Pressure-time curves by three velocities of gas recovery and injection

将上述 3种荷载-时间历程曲线分别加载于储库腔体内表面，进行瞬态力学计算并进行可靠性分析，结果如表4。

表4 不同注采速率下的储气库状况比较(运行30 a)Table 4 Comparison of storage conditions with different velocities of gas recovery and injection (operating 30 years)

以上结果表明，增大注采速率将加速储气库的破坏，而适当降低注采速率可抑制腔体收缩，有利于提高储气库的稳定性。

5 结 论

（1）腔体在长期周期性荷载作用下，围岩将发生流变，在低压阶段及注采气阶段，腔体位移变化较为明显；随着时间的增加，腔体内压的周期性变化对腔体节点位移变化速率的影响逐渐减弱。

（2）将储气库围岩参数等风险因素视为服从某分布的随机变量，以体积收缩作为评判其失效概率的依据，建立储气库正常运行期功能函数，计算分析在长期周期性内压的作用下，储气库失效概率的变化规律，根据储气库失效概率曲线，将储气库运营期分为低失效概率稳定期（1～5 a）、失效概率迅速增长期（5～20 a）、高失效概率稳定期（20 a以后）。

（3）通过改变腔体内压的荷载-时间历程曲线，探讨了正常运行期间注采气速率对储气库稳定的影响。计算结果显示，增大注采气速率将加速储气库的破坏，而适当降低注采气速率可抑制腔体收缩，有利于提高储气库的稳定性。上述结果可为盐岩储气库长期安全运营提供技术支持。

[1]American Gas Association. Survey of underground storage of natural gas in the United States and Canada[R].Arlington, USA: America Gas Association, 1996.

[2]杨春和. 深部盐岩层地下石油储备中的基础性研究[R].武汉: 中国科学院武汉岩土力学研究所, 2008.

[3]张应迁, 张洪才. ANSYS有限元分析从入门到精通[M].北京: 人民邮电出版社, 2010.

[4]陈卫忠, 谭贤君, 伍国军, 等. 含夹层盐岩储气库气体渗透规律研究[J]. 岩石力学与工程学报, 2009, 28(7):1298－1304.CHEN Wei-zhong, TAN Xian-jun, WU Guo-jun, et al.Research on gas seepage law in laminated salt rock gas storage[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7): 1297－1304.

[5]杨春和, 梁卫国, 魏东吼, 等. 中国盐岩能源地下储存可行性研究[J]. 岩石力学与工程学报, 2005, 24(24):4409－4417.YANG Chun-he, LIANG Wei-guo, WEI Dong-hou, et al.Investigation on possibility of energy storage in salt rock in China[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(24): 4409－4417.

[6]杨春和, 李银平, 陈峰. 层状盐岩力学理论与工程[M].北京: 科学出版社, 2009.

[7]吴文, 杨春和, 侯正猛. 盐岩中能源(石油和天然气)地下储存力学问题研究现状及其进展[J]. 岩石力学与工程学报, 2005, 24(增刊2): 5561－5568.WU Wen, YANG Chun-he, HOU Zheng-meng.Investigation on studied situations association with mechanical aspects and development for underground storage of petroleum and natural gas in salt rock[J].Chinese Journal of Rock Mechanics and Engineering,2005, 24(Supp. 2): 5561－5568.

[8]BEREST P, BROUARD B. Safety of salt caverns used for underground gas[J]. Oil & Gas Science and Technology,2003, 58(3): 361－384.

[9]王渭明. 岩石力学[M]. 徐州: 中国矿业大学出版社，2009.

[10]吴世伟. 结构可靠度分析[M]. 北京: 人民交通出版社,1990.

[11]贾超, 张强勇, 张宁, 等. 盐岩地下储气库风险分级机制初探[J]. 岩土力学, 2009, 30(12): 3621－3026.JIA Chao, ZHANG Qiang-yong, ZHANG Ning, et al.Preliminary research of risk classification for underground salt rock gas storage[J]. Rock and Soil Mechanics, 2009, 30(12): 3621－3626.

[12]张强勇, 刘德军, 贾超, 等. 盐岩油气储库介质地质力学模型相似材料的研制[J]. 岩土力学, 2009, 30(12):3581－3586.ZHANG Qiang-yong, LIU De-jun, JIA Chao, et al.Development of geomechanical model similitude material for salt rock oil-gas storage medium[J]. Rock and Soil Mechanics, 2009, 30(12): 3581－3586.

[13]刘家涛. 盐岩地下储气库（群）运营期可靠度计算及风险评估[D]. 济南: 山东大学, 2011.

[14]陈锋, 杨春和, 白世伟. 盐岩储气库最佳采气速率数值模拟研究[J]. 岩土力学, 2007, 28(1): 57－62.CHEN Feng, YANG Chun-he, BAI Shi-wei. Investigation on optimized gas recovery velocity of natural gas storage in salt rock layer by numerical simulation[J]. Rock and Soil Mechanics, 2007, 28(1): 57－62.